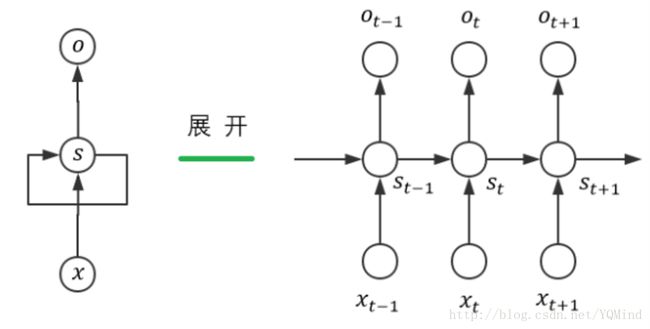
RNN里的BPTT算法
这两天对RNN循环神经网络进行了学习，由一无所知到现在对什么是RNN以及它的前向传播和反向传播有了认识，尤其是BPTT算法的推导有些繁琐，但是推过一次后，对RNN反向传播求梯度的过程有了更清晰的认识。
下面是朴素的RNN循环神经网络图。（图1）
我在写博客前，自己先手写了一份推导过程。（图2）
为何BPTT更难？
因为多了状态之间的传递（即隐层单元之间的“交流”），根据前向传播算法，我们知道 s t ∗ = W s t − 1 + U x t , s_t^* = Ws_{t-1} + Ux_t , st∗=Wst−1+Uxt, 而 s t − 1 = f ( s t − 1 ∗ ) = f ( W s t − 2 + U x t − 1 ) s_{t-1} = f(s_{t-1}^*) = f(Ws_{t-2}+Ux_{t-1}) st−1=f(st−1∗)=f(Wst−2+Uxt−1),这说明 s t − 1 s_{t-1} st−1也是关于 W W W的式子。
这样层层嵌套下去…就会追溯到 s 0 s_0 s0。可以意识到我们对 W 、 U W、U W、U的梯度求解是繁琐的，而这正是BPTT的难点所在。对于 V V V的梯度求解，并没有受到状态之间传递的影响，因此和我们BP算法求解方式是一样的。
我们用 ∗ * ∗表示element-wise, × × ×表示矩阵乘法。
我们采用交叉熵损失函数，即 L t = − ( y t l o g ( o t ) + ( 1 − y t ) l o g ( 1 − o t ) ) L_t = - (y_tlog(o_t)+(1-y_t)log(1-o_t)) Lt=−(ytlog(ot)+(1−yt)log(1−ot))
我们定义隐藏层的激活函数为sigmoid函数 s t = f ( s t ∗ ) s_t = f(s_t^*) st=f(st∗),输出层的激活函数也为sigmoid函数 o t = g ( o t ∗ ) o_t = g(o_t^*) ot=g(ot∗)。 f ′ = s t ∗ ( 1 − s t ) , g ′ = o t ∗ ( 1 − o t ) f' = s_t*(1-s_t), g' = o_t*(1-o_t) f′=st∗(1−st),g′=ot∗(1−ot) 。具体求导读者自行证明。
由前向传播可知， o t = g ( o t ∗ ) = g ( V s t ) o_t = g(o_t^*)=g(Vs_t) ot=g(ot∗)=g(Vst)
那么 ∂ L t ∂ V = ∂ L t ∂ o t ∗ ∂ o t ∂ o t ∗ ⋅ ∂ o t ∗ ∂ V = − ( y t o t + y t − 1 1 − o t ) ∗ o t ∗ ( 1 − o t ) ⋅ ∂ o t ∗ ∂ V = ( o t − y t ) × s t T \frac{\partial L_t}{\partial V} = \frac{\partial L_t}{\partial o_t}* \frac{\partial o_t}{\partial o_t^*}·\frac{\partial o_t^*}{\partial V} = -(\frac{y_t}{o_t}+\frac{y_t-1}{1-o_t})*o_t*(1-o_t)·\frac{\partial o_t^*}{\partial V} = (o_t-y_t)×s_t^ \mathrm{ T } ∂V∂Lt=∂ot∂Lt∗∂ot∗∂ot⋅∂V∂ot∗=−(otyt+1−otyt−1)∗ot∗(1−ot)⋅∂V∂ot∗=(ot−yt)×stT
不同时刻的 ∂ L t ∂ V \frac{\partial L_t}{\partial V} ∂V∂Lt要相加，得到最后的 ∂ L ∂ V \frac{\partial L}{\partial V} ∂V∂L。
由前向传播可知，对于时刻t而言， s t − 1 s_{t-1} st−1也是关于 W W W的式子，因此我们在求 ∂ L t ∂ W \frac{\partial L_t}{\partial W} ∂W∂Lt时，不能简单的将 s t − 1 s_{t-1} st−1视为常量，因此 ∂ L t ∂ W = ∑ k = 0 t ∂ L t ∂ s k ∗ × s k − 1 T \frac{\partial L_t}{\partial W} = \sum_{k=0}^t \frac{\partial L_t}{\partial s_k^*}×s_{k-1}^ \mathrm{ T } ∂W∂Lt=∑k=0t∂sk∗∂Lt×sk−1T(注意，在我这里是把第一个时刻从0开始)。
∂ L t ∂ s t ∗ = ∂ L t ∂ o t ∗ ⋅ ∂ o t ∗ ∂ s t ∗ = V T × ( o t − y t ) ∗ s t ∗ ( 1 − s t ) \frac{\partial L_t}{\partial s_t^*} = \frac{\partial L_t}{\partial o_t^*}· \frac{\partial o_t^*}{\partial s_t^*}= V^\mathrm{T}×(o_t-y_t)*s_t*(1-s_t) ∂st∗∂Lt=∂ot∗∂Lt⋅∂st∗∂ot∗=VT×(ot−yt)∗st∗(1−st)
∂ L t ∂ s k − 1 ∗ = ∂ L t ∂ s k ∗ ⋅ ∂ s k ∗ ∂ s k − 1 ∗ ∂ s k − 1 ∂ s k − 1 ∗ = s k − 1 ∗ ( 1 − s k − 1 ) ∗ W T × ∂ L t ∂ s k ∗ ( k = 1 , 2 , 3... t ) \frac{\partial L_t}{\partial s_{k-1}^*} = \frac{\partial L_t}{\partial s_k^*}· \frac{\partial s_k^*}{\partial s_{k-1}}*\frac{\partial s_{k-1}}{\partial s_{k-1}^*}= s_{k-1}*(1-s_{k-1})*W^\mathrm{T}×\frac{\partial L_t}{\partial s_k^*} (k=1,2,3...t) ∂sk−1∗∂Lt=∂sk∗∂Lt⋅∂sk−1∂sk∗∗∂sk−1∗∂sk−1=sk−1∗(1−sk−1)∗WT×∂sk∗∂Lt(k=1,2,3...t)
同理， ∂ L t ∂ U = ∑ k = 0 t ∂ L t ∂ s k ∗ × x k T \frac{\partial L_t}{\partial U} = \sum_{k=0}^t \frac{\partial L_t}{\partial s_k^*}×x_{k}^ \mathrm{ T } ∂U∂Lt=∑k=0t∂sk∗∂Lt×xkT。
最后不同时刻的 ∂ L t ∂ U \frac{\partial L_t}{\partial U} ∂U∂Lt要相加，得到最终的 ∂ L ∂ U = ∑ t = 0 t = n ∂ L t ∂ U \frac{\partial L}{\partial U}= \sum_{t=0}^{t=n} \frac{\partial L_t}{\partial U} ∂U∂L=∑t=0t=n∂U∂Lt
最后不同时刻的 ∂ L t ∂ W \frac{\partial L_t}{\partial W} ∂W∂Lt要相加，得到最终的 ∂ L ∂ W = ∑ t = 0 t = n ∂ L t ∂ W \frac{\partial L}{\partial W}= \sum_{t=0}^{t=n} \frac{\partial L_t}{\partial W} ∂W∂L=∑t=0t=n∂W∂Lt
[1] https://blog.csdn.net/zhaojc1995/article/details/80572098