indeed2017校招在线编程题（网测）二

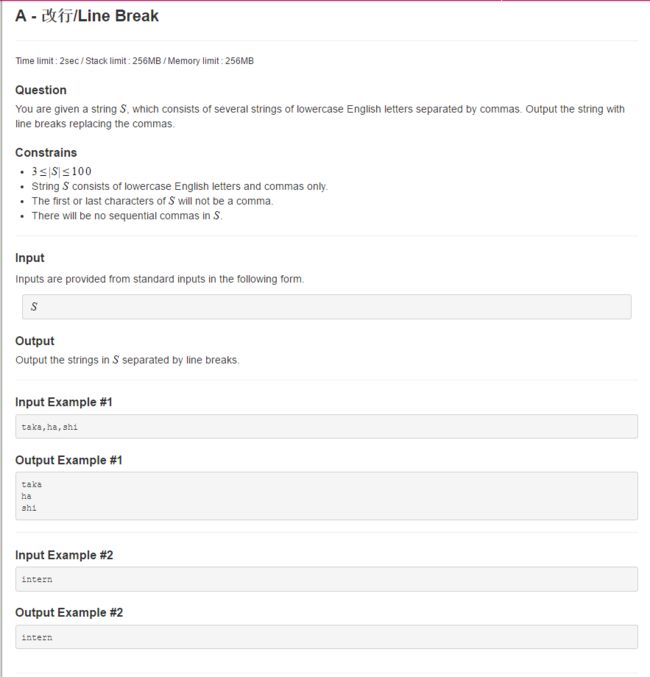
A - 改行/Line Break

解题思路
水题

import java.util.Scanner;

public class Main{
    public static void main(String []args){
        Scanner cin=new Scanner(System.in);
        while(cin.hasNext()){
            String s=cin.nextLine();
            String[]str=s.split(",");
            for(String e:str){
                System.out.println(e);
            }
        }
    }
}

B - 順列/Permutations

解题思路
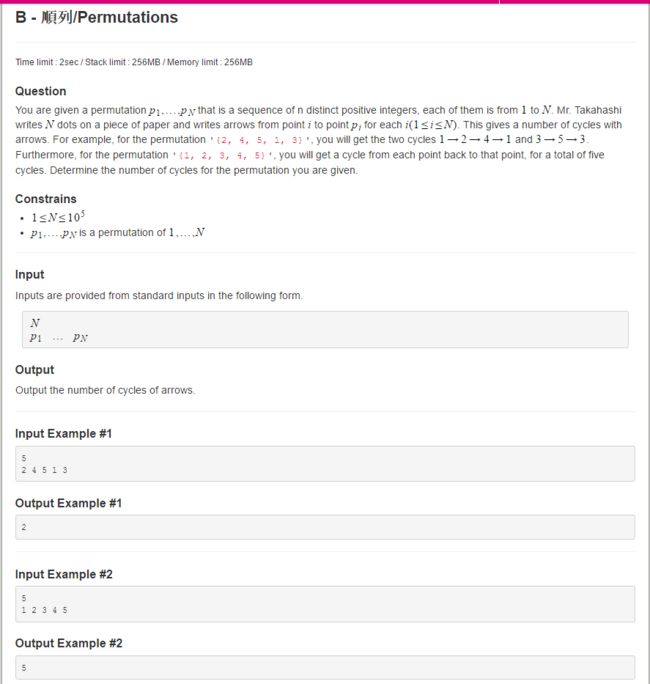
水题，问你有几个cycles。
如(2,4,5,1,3)，每个节点分别指向(1,2,3,4,5)，即2-1,4-2,5-3,1-4,3-5。遍历一下，就可以得到两个cycles(2-1-4-2),(5-3-5)。
下面代码中，p为当前节点，flag为每个节点所在的环。类dfs，从某个节点出发，标记经过的节点为同一个环，直到经过的节点已被标记过，则遍历下一个节点，并标记下一个环。

import java.util.Scanner;

public class Main{
    public static void main(String []args){
        Scanner cin=new Scanner(System.in);
        while(cin.hasNext()){
            int n=cin.nextInt();
            int[]p=new int[n+1];
            int []flag=new int[n+1];
            for(int i=1;i<=n;i++)
                p[i]=cin.nextInt();
            int res=1;
            for(int i=1;i<=n;i++){
                if(flag[i]==0){
                    int j=i;
                    while(flag[j]==0){
                        flag[j]=res;
                        j=p[j];
                    }
                    res++;
                }
                /*for(int j=1;j<=n;j++)System.out.print(flag[j]+" " );
                System.out.println();*/
            }
            System.out.println(res-1);
        }
    }
}

C - マス目と駒/Tables and Pieces

解题思路
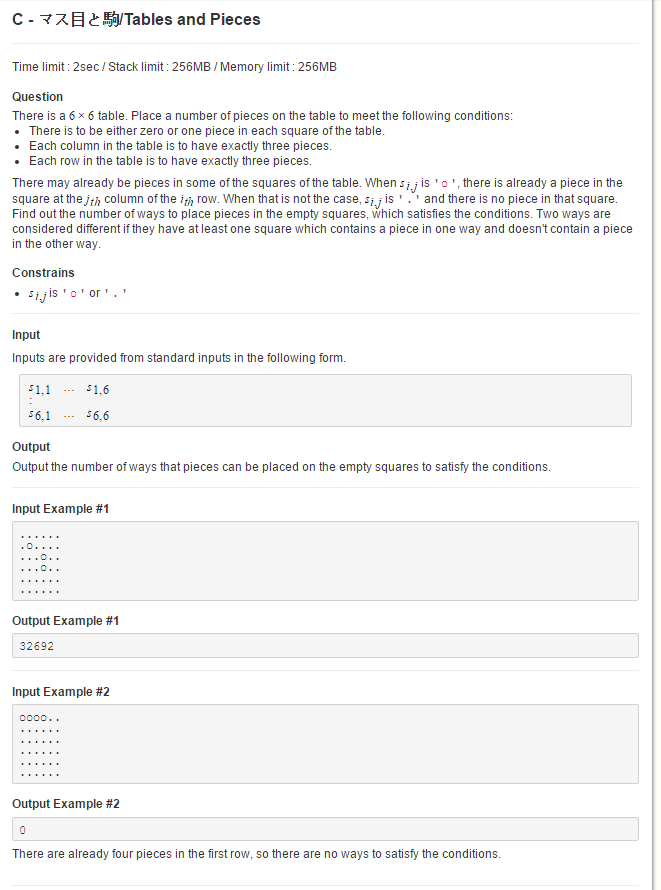
输入一个6X6的表，其中’o’表示已经有一个piece，’.’表示没有。要求每行每列都有3个’o’，求不同的摆放方法数目。
使用dfs。。。。

import java.util.Scanner;

public class Main{
    private static int res=0;
    public static void dfs(int[][]s,int[]row,int[]col,int idx,int jdx){
        if(idx==6){
            boolean flag=true;
            for(int i=0;i<6;i++)
                if(col[i]!=3||row[i]!=3){
                    flag=false;
                    break;
                }
            if(flag){
/*              for(int i=0;i<6;i++){
                    for(int j=0;j<6;j++)
                        System.out.print(s[i][j]+" ");
                    System.out.println();
                }
                System.out.println();*/
                res++;
            }
            return ;
        }
        if(row[idx]==3){
            dfs(s,row,col,idx+1,0);
        }
        for(int i=jdx;i<6;i++){
            if(s[idx][i]==0&&col[i]<3){
                row[idx]++;
                col[i]++;
                s[idx][i]=1;
                dfs(s,row,col,idx,i);
                s[idx][i]=0;
                row[idx]--;
                col[i]--;
            }
        }
    }
    public static void main(String []args){
        Scanner cin=new Scanner(System.in);
        while(cin.hasNext()){
            int[][]s=new int[6][6];
            int row[]=new int[6];
            int col[]=new int[6];
            for(int i=0;i<6;i++){
                String str=cin.nextLine();
                for(int j=0;j<6;j++){
                    if(str.charAt(j)=='.')s[i][j]=0;
                    if(str.charAt(j)=='o'){
                        s[i][j]=1;
                        row[i]++;
                        col[j]++;
                    }
                }
            }
            boolean flag=false;
            for(int i=0;i<6;i++){
                if(row[i]>3||col[i]>3){
                    //System.out.println(0);
                    flag=true;
                }
            }
            if(flag){
                System.out.println(0);
                continue;
            }
            res=0;
            dfs(s,row,col,0,0);
            System.out.println(res);
        }
    }
}

D - 色付きボール/Colored Balls

解题思路
这道没做出来，只做对了k=2的情况。k=2的时候，就相当于两个几何分布。
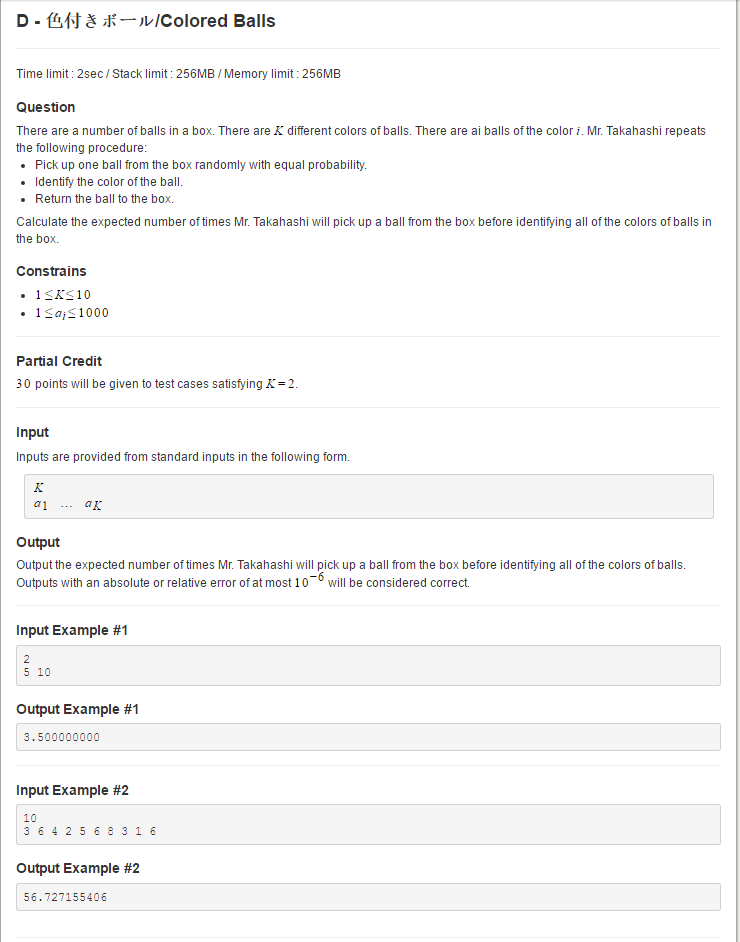
题目意思是一个箱子里有一些球，这些球是有颜色的，一共有k个不同颜色。Mr Takabashi 重复一下步骤：
- 从box里随机拿出一个球
- 辨别这个球的颜色
- 将这个球放回box里
问Mr Takabashi需要平均从box里取几次（即期望值）才能知道k个颜色是哪些，即平均取多少次才能至少取到K个具有不同颜色的球。
设p(N=n)表示取n次时可辨别k个颜色的概率。
当k=2时，则n>=2。p1表示取到的球为颜色1的概率，p2表示取到的球为颜色2的概率，有放回的取，故p1+p2=1.
P(N=2)=p1 x p2
P(N=3)=(p1)^2 x p2+(p2)^2 x p1
…
P(N=n)=(p1)^(n-1) x p2+(p2)^(n-1) x p1
可以将其看作两个（受限的）独立的几何分布（至少2次）：不断取球，直到取到颜色1停止；不断取球，直到取到颜色2停止；
几何分布概念：在n次伯努利试验中，前k-1次皆失败，第k次成功的概率。
K>2时，感觉是和K-1递推过去。。具体怎么做，没想出来。。。

import java.util.Scanner;
public class Main{
    public static void main(String[]args){
        Scanner cin=new Scanner(System.in);
        while(cin.hasNext()){
            int k=cin.nextInt();
            int []a=new int[k];
            for(int i=0;idouble res=0;
            if(k==2){
                double a1=a[0]*1.0/(a[0]+a[1]);
                double b1=a[1]*1.0/(a[0]+a[1]);
                res=(a1*2-a1*a1)/(1-a1)+(b1*2-b1*b1)/(1-b1);
                System.out.println(res);
            }
        }
    }
}