2019.10.07日常总结

无论你愿意不愿意，明天开学了！！！

洛谷P3939：

【题意】：
$n$ 只兔子，颜色分别是 $a_1$ 到 $a_n(a_i\le 3\times 10^5)$。
$m$次操作，每次操作
$1$ $l$ $r$ $c$：询问$[l,r]$区间有多少颜色为 $c$ 的兔子
$2$ $x$：$x$ 和 $x+1$ 这两只兔子交换了颜色
对于每次操作询问答案
【数据范围】：

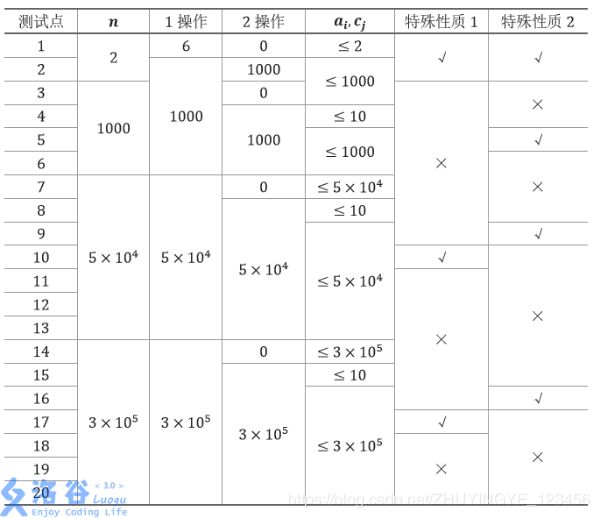
【思路】：
令$g[x]$记录所有颜色为$x$的兔子的位置

输入部分：

for(i=1;i<=n;i++){
	a[i]=read();
	g[a[i]].push_back(i);
}

对于操作$1$：

y=read();z=read();
int k1=lower_bound(g[z].begin(),g[z].end(),x)-g[z].begin();
int k2=upper_bound(g[z].begin(),g[z].end(),y)-g[z].begin()-1;
if (k1>k2) printf("0\n");//注意特判
else printf("%d\n",k2-k1+1);

对于操作$2$：

if (a[x]==a[x+1]) continue;
int k1=lower_bound(g[a[x]].begin(),g[a[x]].end(),x)-g[a[x]].begin();
g[a[x]][k1]++;
int k2=lower_bound(g[a[x+1]].begin(),g[a[x+1]].end(),x+1)-g[a[x+1]].begin();
g[a[x+1]][k2]--;
swap(a[x],a[x+1]);

【代码】：

#include 
using namespace std;
#define gc getchar()
#define g(c) isdigit(c)
inline int read(){
	char c=0;int x=0;bool f=0;
	while (!g(c)) f=c=='-',c=gc;
	while (g(c)) x=x*10+c-48,c=gc;
	return f?-x:x;
}
const int N=3e5+1e3;
vector<int> g[N];
int a[N],i,x,y,z,n,m,opt;
int main(){
	freopen("t1.in","r",stdin);
	n=read();m=read();
	for(i=1;i<=n;i++){
		a[i]=read();
		g[a[i]].push_back(i);
	}
	for(i=1;i<=m;i++){
		opt=read();x=read();
		if (opt==1){
			y=read();z=read();
			int k1=lower_bound(g[z].begin(),g[z].end(),x)-g[z].begin();
			int k2=upper_bound(g[z].begin(),g[z].end(),y)-g[z].begin()-1;
			if (k1>k2) printf("0\n");
			else printf("%d\n",k2-k1+1);
		}
		else{
			if (a[x]==a[x+1]) continue;
			int k1=lower_bound(g[a[x]].begin(),g[a[x]].end(),x)-g[a[x]].begin();
			g[a[x]][k1]++;
			int k2=lower_bound(g[a[x+1]].begin(),g[a[x+1]].end(),x+1)-g[a[x+1]].begin();
			g[a[x+1]][k2]--;
			swap(a[x],a[x+1]);
		}
	}
	return 0;
}

P1528 切蛋糕 P2329 栅栏

（两题本质是一样的，所以我一起写了）

【题意】：
你有$n(n\le 50)$块蛋糕，每块蛋糕有单独的大小$(x\le 32767)$，你要满足$m(m\le 1000)$个人，每个人想恰好吃到$a_i$大小的蛋糕，你可以任意分割蛋糕，但不能合并，求最多能满足多少人
【思路】：
首先，本题的答案满足单调性，即可以满足$k$个人，一定可以满足$k-1$个人。所以我们使用二分，二分答案$mid$，表示可以满足$mid$个人
考虑使用$dfs$判断$mid$是否可行
当然，原始的$dfs$会$T$，所以我们要剪枝
剪枝$1$：按每个人需要的蛋糕从小到大排序，因为满足小的肯定比满足大的优
剪枝$2$：记录一个浪费值$waste$，当一个蛋糕被分了后<最小的蛋糕需要，则$waste+=$蛋糕剩余大小。当所有蛋糕$-waste<mid$个人的需要，则剪枝
剪枝$3$：当两个人的需要一样时，只考虑一个人即可。
（注：本思路为$P1528$题的思路，对于$P2329$题，请读者自己理解）
【代码】：

#include 
using namespace std;
int len[55],t[55];
int waste,need[1010];
int a[1010],sum,n,m;
int l,r,mid,ans,i;
bool dfs(int x,int part){
	if (x==0) return true;
	if (sum-waste<a[mid])
		return false;
//	剪枝1：当总量-浪费<需要时，剪枝 
	for(int i=part;i<=n;i++)
	if (t[i]>=need[x]){
		t[i]-=need[x];
		if (t[i]<need[1])
			waste+=t[i];
//		当一个木板剩余长度<最小需要时，浪费 
		if (need[x]==need[x-1]){
			if (dfs(x-1,i)) return true;
		}
		else if (dfs(x-1,1)) return true;
		if (t[i]<need[1])
			waste-=t[i];
		t[i]+=need[x];
	}
	return false;
}
inline int binary_search(){
	l=mid=ans=0;r=m;
	while (l<=r){
		mid=(l+r)>>1;waste=0;
		memcpy(t,len,sizeof(t));
		if (dfs(mid,1)){
			l=mid+1;
			ans=mid;
		}
		else r=mid-1;
	}
	return ans;
}//笔者最推荐的二分写法
int main(){
//	freopen("t1.in","r",stdin);
	scanf("%d",&n);
	for(i=1;i<=n;i++){
		scanf("%d",&len[i]);
		sum+=len[i];
	}
	scanf("%d",&m);
	for(i=1;i<=m;i++)
	scanf("%d",&need[i]);
	sort(need+1,need+m+1);
	while (sum<need[m]) m--;
	for(i=1;i<=m;i++)
	a[i]=a[i-1]+need[i];
	cout<<binary_search();
	return 0;
}

注：本日记的思路重要来源于洛谷网校老师的讲解，若有侵权，请联系笔者，笔者立即删除！