C++高级数据结构算法 | Tire树（字典树、前缀树）

在LeetCode刷题遇到了设计Tire树的题目，于是花了一些时间研究了一下Trie树（也称前缀树、字典树），正如书上所言，这是人类对算法研究的最高成果之一，自己通过查阅资料，学习了网上很多有关Trie树的优秀博文，自己编写了基于C++语言的完整Trie树实现，接下来主要结合实现代码向大家分享这一优秀的数据结构。

---

---

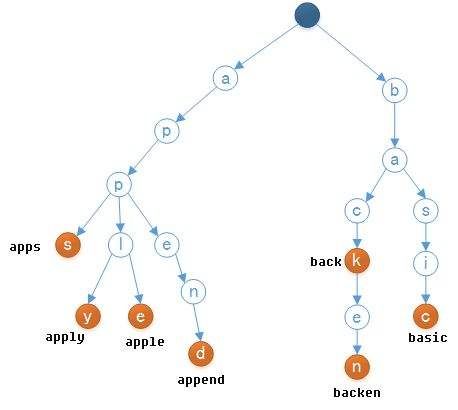
Trie树的基本概念

Trie树，即字典树，又称单词查找树、前缀树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。

Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

它有3个基本性质：

• 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
• 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
• 每个节点的所有子节点包含的字符都不相同。

---

Trie树的应用场景

字典树查找效率很高，时间复杂度是$O(n)$，$n$ 是要查找的单词中包含的字母的个数，但是会浪费大量存放空指针的存储空间，属于以空间换时间的算法。

1、串快速检索

给出N个单词组成的熟词表，以及一篇全用小写英文书写的文章，请你按最早出现的顺序写出所有不在熟词表中的生词。

2、单词自动完成

编辑代码时，输入字符，自动提示可能的关键字、变量或函数等信息。

3、最长公共前缀

对所有串建立字典树，对于两个串的最长公共前缀的长度即他们所在的结点的公共祖先个数，于是，问题就转化为最近公共祖先问题。

4、串排序方面的应用

给定N个互不相同的仅由一个单词构成的英文名，让你将他们按字典序从小到大输出用字典树进行排序，采用数组的方式创建字典树，这棵树的每个结点的所有儿子很显然地按照其字母大小排序。对这棵树进行先序遍历即可。

---

根据上述的讲解，自己使用C++语言实现了Trie树结构，经过了基本功能测试、内存泄露检测等单元测试，接下来进行模块分析。

---

Trie树的结构定义

有关Trie树结构定义有很多不同版本，具体要根据实现的功能而定，在这里我们实现如下几个重要的操作：

• 插入操作（单词插入）
• 删除操作（单词删除）
• 单词搜索
• 指定前缀搜索
• 前缀次数查询
• 销毁操作

---

下面是结构定义：

/** 
 * 定义每个子树的最大分支数目 a - Z  65 - 122
 * 我们实现的Trie树存储是string类型的单词，那么它包括大写和小写字母
 * 为了提高代码的可读性，我们直接将对应的单词直接存储到其ascll值的位置，
 * 但是注意的是，这并不是最优的方法，一般来说，我们为了节省空间，都会充分
 * 利用存储空间进行元素存储，例如，应将小写a存储在 a - 'a'的位置。
 */
const int MaxBranchNum = 123;

/**
 * Trie树节点定义
 */
class TrieNode
{
public:
	/* 单词完整标志位 */
	bool isWord;
	/* 结点存储的字符 */
	char word;
	/* 有多少单词通过这个节点,即由根至该节点组成的字符串模式出现的次数 */
	int count;
	/* next数组存储所有的子节点 */
	TrieNode* next[MaxBranchNum]; 
public:
	/* 结点初始化 */
	TrieNode(char word = 0)
	{
		this->word = word;
		isWord = false;
		count = 1; // 每个字符初始化就算一个前缀了
		memset(next, 0, sizeof(next)); // 子节点初始化
	}
};

/**
 * Trie树的结构定义
 */
class TrieTree {
public:
	/* Trie树的初始化 */
	TrieTree()
	{
		pRoot = new TrieNode();
	}
	
	/* Trie树的析构 - 调用销毁函数销毁树，释放所有内存 */
	~TrieTree()
	{
		Destory(pRoot);
	}
	
	/* 销毁函数 */
	void Destory(TrieNode* pRoot);
	
	/* 插入函数 - 插入单词 */
	void insert(string str);
	
	/* 删除函数 - 删除单词*/
	bool remove(string str);
	
	/* 查询函数 - 查询完整单词 */
	bool search_Str(string str);
	
	/* 前缀搜索 - 查询指定前缀 */
	bool priSearch_str(string str);
	
	/* 前缀次数搜索 - 查询指定前缀出现的次数 */
	int getPriNum(string str);
	
	/* 辅助函数（删除操作使用） - 获取第k个位置所在的结点 */
	TrieNode* getchNode(string str, int k);

---

Trie树的单词插入

简单描述一下插入算法的设计，Tire树的插入并不复杂，主要步骤如下：

• 首先若次单词存在，则不进行插入操作，我们使用查询函数来完成判断
• 遍历待插入单词的每个字符，并从Trie树的根节点开始逐字符的匹配
• 存在该字符，那么首先将该字符的count成员更新（加1），表示由根至该节点组成的字符串模式出现的次数多了一次，然后继续从下个位置匹配待插入单词的下个字符。直到遍历完成。
• 若在遍历过程中遇到没有该字符的结点，那么我们为此字符开辟一个新的结点存储在其父节点的next域中。
• 当待插入单词的每个字符都遍历完成后，该单词就完整的插入到了Trie树中，我们将最后一个结点的$isword$标志位置为true，表示从根到该结点是一个完整的单词。

void insert(string str)
{
	if (str.length() == 0 || search_Str(str))
		return;
	
	/* curNode 指向Trie树的根节点 */
	TrieNode* curNode = pRoot;
	
	/* 遍历待插入单词的每个字符，并进行插入 */
	for (char str_ch : str)
	{
		/* 在路径中该字符结点存在，更新count域，继续向子节点遍历 */
		if (curNode->next[str_ch] != nullptr)
		{
			curNode = curNode->next[str_ch];
			curNode->count++;
		}
		/**
		 * 在路径中该字符结点不存在，为该字符创建新的结点，
		 * 并继续向子节点遍历
		 */
		else
		{
			TrieNode* newNode = new TrieNode(str_ch);
			curNode->next[str_ch] = newNode;
			curNode = curNode->next[str_ch];
		}
	}
	/* 单词插入完成后，该结点的完整标志位置为true */
	curNode->isWord = true;
}

---

Trie树的单词查找

这是Trie树设计最为巧妙地部分，$Tire$ 树设计的根本意义。无论单词量有多大，我们需要$O(n)$时间即可实现查找过程，其中$n$为单词的长度，其查找效率是其他任何数据结构无法比拟的。

根据我们所定义的结构，$Trie$ 树的单词查找直接从根节点开始，遍历指定单词的所有字符，遍历结束后，若当前结点不为空并且其单词完整标志位为 $true$，则表示单词存在。

bool search_Str(string str)
	{
		if (str.length() == 0)
		{
			return false;
		}
		/* curNode 指向Trie树的根节点 */
		TrieNode* curNode = pRoot;
		/* 遍历指定查询单词的每个字符，并进行插入 */
		for (char str_ch : str)
		{
			/* 当前结点不为空，则curNode继续走向子节点匹配下个字符 */
			if (curNode != nullptr)
			{
				curNode = curNode->next[str_ch];
			}
		}
		
		/* 若当前结点不为空并且其单词完整标志位为true，则表示单词存在。*/
		return (curNode != nullptr && curNode->isWord);
	}

---

Trie树的前缀查询

Trie树又称为前缀树，因此，Trie树在海量数据中进行前缀搜索效率是非常之高的，同样只需要$O(n)$时间即可完成搜索过程。

具体的实现和查找操作基本是相同的，唯一不同的地方在于，在遍历完指定前缀的所有字符后，若当前结点不为空，则表示前缀存在，而不用判断其完整标志位是否为 $true$。

bool priSearch_str(string str)
	{
		if (str.length() == 0)
		{
			return false;
		}
		/* curNode 指向Trie树的根节点 */
		TrieNode* curNode = pRoot;
		/* 遍历指定前缀的每个字符，并进行插入 */
		for (char str_ch : str)
		{
			/* 当前结点不为空，则curNode继续走向子节点匹配下个字符 */
			if (curNode != nullptr)
			{
				curNode = curNode->next[str_ch];
			}
		}
		/* 若当前结点不为空，则表示前缀是存在的，返回true。*/
		return (curNode != nullptr);
	}

---

Trie树的前缀次数查询

Trie树在海量数据中也可以快速地统计出指定前缀的单词个数，搜索效率很高，只需要$O(n)$时间即可完成统计过程。

为了实现高效的查询算法，我们在设计之初就给$Trie$树的每个结点都提供了一个$count$成员存储有多少单词再插入过程中经过了该结点（也就是单词前缀）。因此，在前缀次数查询函数中我们其实并没有真正的去统计指定前缀的单词个数，而是直接返回$count$中存储的信息即可，具体实现就是我们遍历到指定前缀的最后一个字符位置，输出其$count$信息即可。

int getPriNum(string str)
	{
		if (str.length() == 0)
		{
			return 0;
		}
		/* 如果该前缀没有出现过，直接返回0 */
		if (!priSearch_str(str))
			return 0;
		/* curNode 指向Trie树的根节点 */
		TrieNode* curNode = pRoot;
		
		for (char str_ch : str)
		{
			/* 当前结点不为空，则curNode继续走向子节点匹配下个字符 */
			if (curNode != nullptr)
			{
				curNode = curNode->next[str_ch];
			}
		}
		/* 直接返回当前结点的count */
		if(curNode != nullptr)
			return curNode->count;
		return 0;
	}

---

Trie树的单词删除算法

Trie树的单词删除算法相对于其他操作来说，是最为复杂的操作了，因为涉及到节点中成员的修改，next的修改等等。但是只要我们将各类情景都考虑全面的，代码也是很容易实现的。

接下来我们分析一下，删除单词的几种情况。

• 待删除的元素不仅是完整的单词，也是其他单词的前缀，那么这种情况下，我们就并不需要删除它，只是将其单词完整标志位置为false、并且向上回溯并count更新（减 1） 即可，表示从根到该结点将不再是一个单词了。
• 那么当待删除的元素不是一个前缀，那么我们也不可以直接按节点删除，因为有可能待删除结点的某个前缀也是其他单词的前缀，那么这时候我们只需从下向上遍历（对应于单词来讲就是从后向前遍历），遍历到某个结点的$count$域不为1后，继续向上回溯将其前缀结点的count域更新（减一），否则$count$域为1就可以放心的删除该结点。注意这里我们不能真正的删除该结点，即不能使用delete删除结点，而仅仅是将该结点置为nullptr即可，因为我们还要保证下次可以继续使用该结点，并且保证析构函数的正确执行。
• 当我们遍历到的$count$域不为1的结点后，还需要更新其$count$域（原基础上减一），并且继续向上回溯到根（准确的说是根下的数据节点）。
• 我们还要注意这一种情况，待删除单词在$Tire$ 树中的路径无分支，即我们在删除完所有的结点后，需要将根节点指向删除结点元素首字符的$next$数组置空。

由上述分析我们得到，单词元素的删除是自底向上的，我们需要得到对应位置的节点，因此建立了辅助函数 $getchNode()$ 来返回待删除结点的第 k 个字符所在的结点。

TrieNode* getchNode(string str, int k)
{
	/* curNode 指向Trie树的根节点 */
	TrieNode* curNode = pRoot;

	for (char str_ch : str)
	{
		/* 遍历到第k个元素直接跳出循环 */
		if (k-- == 0)
			break;
			
		/* 当前结点不为空，则curNode继续走向子节点匹配下个字符 */
		if (curNode != nullptr)
		{
			curNode = curNode->next[str_ch];
		}
	}
	/* 返回第k个字符所在的结点 */
	return curNode;
}

bool remove(string str)
{
	/* 通过search_Str查询函数判断Tire树中是否存在str 不存在返回false */
	if (str.length() == 0 || !search_Str(str))
	{
		return false;
	}

	/** 
	* 如果以str为前缀的单词个数超过1，那么我们并不是真正删除该单词
	 * 而是只是该单词最后一个字符的isword域置false，表示它将不再
	 * 是个完整单词。但是其他单词是以它为前缀的，仍然存在于Trie树中
	 * 请注意，我们还需要向上回溯到根，更新每个结点的count成员
	 */
	if (getPriNum(str) > 1)
	{
		int k = str.size();
		TrieNode* Lastnode = getchNode(str, k);
		Lastnode->isWord = false;

		while (Lastnode != pRoot)
		{
			Lastnode->count--;
			Lastnode = getchNode(str, --k);
		}
		return true;
	}
	/* 更新根节点标志位 */
	bool updateRoot = false;
	
	/* 如果该字符的前缀不影响任何其他元素，str[0]的前缀次数为1，表示删除单词的
	 * 路径没有其他分支，该单词的所有结点都将删除，但是最后要更新root结点相应
	 * 的next域
	 */
	if (getPriNum(str.substr(0, 1)) == 1)
	{
		updateRoot = true;
	}
	
	/* curNode 指向Trie树的根节点 */
	TrieNode* curNode = pRoot;
	
	/* 从后向前遍历待删除的单词 */
	int k = str.size();
	auto it = str.rbegin();
	while (it != str.rend())
	{
		char str_ch = *it;
		
		/* 拿到字符所对应的相应结点 */
		TrieNode* delNode = getchNode(str, k--);

		/**
		 * count域为1并且当前结点不是根节点，就进行结点删除操作
		 * 请注意，这里我们不能真正的删除该结点，即不能使用delete
		 * 删除结点，而仅仅是将该结点置为nullptr即可，因为我们还要
		 * 保证下次可以继续使用该结点，并且保证析构函数的正确执行
		 * 请注意，当
		 */
		if (delNode->count == 1 && delNode != pRoot)
		{
			if (updateRoot)
			{
				free(delNode);
			}
			delNode = nullptr;
		}
		/**
		 * 否则count域不为1则向上不断回溯将相应结点的count的域减一,
		 * 即更新删除结点的前缀结点的count域
		 */
		else
		{
			delNode->count -= 1;
		}
		++it;
	}
	
	/* 更新root根节点 */
	if (updateRoot)
	{
		pRoot->next[str[0]] = nullptr;
	}

	return true;
}

---

Tire树的销毁操作

虽然Tire树的查询效率很高效的，但是其空间的开销也是很大的，因此我们有必要提供销毁函数释放树所占用的空间，在本程序中它是自动完成的，在析构函数中调用销毁操作函数。

代码实现如下：

/* 析构函数 */
~TrieTree()
{
	Destory(pRoot);
}

/* 销毁树 */
void Destory(TrieNode* pRoot)
{
	if (pRoot == nullptr)
		return;
	
	for (int i = 0; i < MaxBranchNum; i++)
	{
		if (pRoot->next[i] != nullptr)
		{
			/* 不断递归地将所有空间释放 */
			Destory(pRoot->next[i]);
		}
	}

	delete pRoot; /* 子节点全部删除后便可以释放根节点 */
	pRoot = nullptr;
	return;
}

---

LeetCode 208. 实现 Trie (前缀树) 题解

基于题目实现如下代码，比我们上述讲解的完整的Trie树要简单很多，因为只有三个简单的操作，并且题目规定只有小写字母（a-z），因此我们next数组定义大小为26即可（节省空间，我们下标按0-26存储）。

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;

const int MAX = 26;
class Trie {
public:
	/* 标识当前结点到根是否组成一个完整的字符串 */
	bool is_str;
	/* 存储下一个结点 */
	Trie* next[MAX];
	/* 存储Trie树的根节点 */
	Trie* pRoot;
	/* 每个结点存储相应的字符 */
	char word_ch;

	/* Root Node Initialize*/
	Trie() {
		is_str = false;
		memset(next, 0, sizeof(next));
		pRoot = this;
	}

	/** Initialize data structure*/
	Trie(char ch) {
		is_str = false;
		memset(next, 0, sizeof(next));
		pRoot = this;
		word_ch = ch;
	}

	/** Inserts a word into the trie. */
	void insert(string word) {
		Trie* cur = pRoot; // cur 指向当前根节点
		for (char ch : word)
		{
			/* 判断该字符是否存在，不存在则新建结点插入 */
			if (cur->next[ch - 'a'] == nullptr)
			{
				Trie* newNode = new Trie(ch);
				cur->next[ch - 'a'] = newNode;
			}
			cur = cur->next[ch - 'a'];
		}
		/* 插入完一个字符，完整标志位置true */
		cur->is_str = true;
	}

	/** Returns if the word is in the trie. */
	bool search(string word) {
		Trie* cur = pRoot; // cur 指向当前根节点
		/* 遍历Trie树查找 */
		for (char w : word)
		{
			if (cur != nullptr)
			{
				cur = cur->next[w - 'a'];
			}
		}
		/* 当前结点不为空并且单词完整时返回true */
		return (cur != nullptr && cur->is_str);
	}

	/** Returns if there is any word in the trie that starts with the given prefix. */
	bool startsWith(string prefix) {
		Trie* cur = pRoot;
		for (char w : prefix)
		{
			if (cur != nullptr)
			{
				cur = cur->next[w - 'a'];
			}
		}
		/* 和search不同就是无需判断单词是否完整 */
		return (cur != nullptr);
	}
};

/**
 * Your Trie object will be instantiated and called as such:
 * Trie* obj = new Trie();
 * obj->insert(word);
 * bool param_2 = obj->search(word);
 * bool param_3 = obj->startsWith(prefix);
 */

//------------------------- Test Code  -----------------------------
int main() {
	Trie* trie = new Trie();
	string str[] = { "zyzmzm","z","ab","zy","zi","abcd","zhaoyang" };
	for (string str : str)
		trie->insert(str);


	cout << trie->search("z");   // true
	cout << trie->startsWith("zyzm"); // true
	cout << trie->startsWith("y");// false
	cout << trie->search("zyzm");  // flase
	cout << trie->search("zyzmzm");  // true

	cout << trie->startsWith("abc"); // true
	cout << trie->search("abc"); // flase
	cout << trie->search("abcd"); // true

	cout << trie->startsWith("yb");// flase
	trie->insert("ybb");
	cout << trie->startsWith("yb");// true
	cout << trie->search("ybb"); // true
	return 0;
}