深入浅出Python机器学习10——数据表达与特征工程

数据表达

• 使用哑变量转化类型特征

       哑变量（Dummy Variables），也称为虚拟变量，是一种在统计学和经济学领域非常常用的，用来把某些类型变量转化为二值变量的方法，在回归分析中的使用尤其广泛。例如我们在之前使用 pandas 的 get_dummies 将 adult 数据集中的类型特征转换成了用 0 和 1 表达的数值特征。
       下例中对 get_dummies 的使用：

       从结果可以看出，pandas 的 DataFrame 生成的一个完整数据集，其中包括整型数值特征 [5, 6, 7, 8]，还包括字符串组成的类型特征 “ 西瓜 ” “ 香蕉 ” “ 橘子 ” “ 苹果 ” 和 “葡萄”。

       继续用 get_dummies 将特征转化为只有 0 和 1 的二值特征，如下：

       从结果可以看出，通过 get_dummies 的转换，之前的类型变量全部变成了只有 0 和 1 的数值变量，或者说是一个稀疏矩阵。数值特征并没有发生变化，这正是 get_dummies 的机智过人之处，它在默认情况下是不会对数值特征进行转化的。

       假如我们希望把数值特征也进行 get_dummies 转换，可以先将数值特征转换为字符串，然后通过 get_dummies 的columns 参数来转换。

       先用 .astype（str）指定了 “ 数值特征 ” 这一列是字符串类型的数据，然后在 get_dummies 中指定 columns 参数为 “ 数值特征 ” 这一列，这样 get_dummies 就只会转化数值特征了。

       实际上，如果不用 fruits[ ‘ 数值特征 ’ ] = [ ‘ 数值特征 ’ ].astype（str）这行代码把数值转化为字符串类型，依然会得到同样的结果。但是在大规模数据集中，还是建议大家进行转化字符串的操作，避免产生不可预料的错误。

• 对数据进行装箱处理

       在机器学习中，不同的算法建立的模型会有很大的差异。即便是在同一个数据集中，这种差别也会存在。这是由于算法的工作原理不同所导致的，如 KNN 和 MLP。如下例：

       在这个例子中分别用 KNN 和 MLP 对数据集进行回归分析，参数都设置为默认值。从图中可以看出 MLP 产生的回归线非常接近线性模型的结果，而 KNN 则相对更复杂一些，试图覆盖更多的点。

       实际中，应该如何选择哪个算法的预测结果？接下来先对数据进行一下 “ 装箱处理 （binning）”，这种方法也称为 “ 离散化处理（discretization） ”。
       由于我们在生成这个实验数据集的时候，是在 -5 到 5 之间随机生成了 50 个数据点，因此我们在生成 “ 箱子 ” （或者说 “ 容器 ”）的时候，也指定范围是从 -5 到 5 之间，生成 11 个元素的等差数列，这样每两个数值之间就形成了一个箱子，一共 10 个。
       从结果可以看出，第一个箱子是 -5 和 -4 之间，第二个箱子是 -4 到 -3 之间，以此类推。第 1 个数据点 -1.1522688 所在箱子是在第 4 个，第 2 个数据点 3.59707847 所在箱子是第 9 个，而第 3 个数据点 4.4419936 所在的箱子是第 10 个，以此类推。
       接下来，我们用新的方法来表达已经装箱的数据，所要用到的方法就是 scikit-learn 的独热编码 OneHotEncoder。OneHotEncoder 和 pandas 的 get_dummies 功能基本是一样的，但是 OneHotEncoder 目前只能用于整型数值的类型变量。如下演示:

       虽然数据集中样本的数量仍是 50 个，但是特征数变成了 10 个。这是因为我们生成的箱子是 10 个，而新的数据点的特征是用其所在的箱子号码来表示的。例如，第 1 个数据点在第 4 个箱子中，则其特征列表中第 4 个数字是 1，其它数字是 0，以此类推。
       这样一来，相当于我们把原先数据集中的连续特征转化成了类别特征。下面继续用 MLP 和 KNN 算法重新进行回归分析，观看变化：

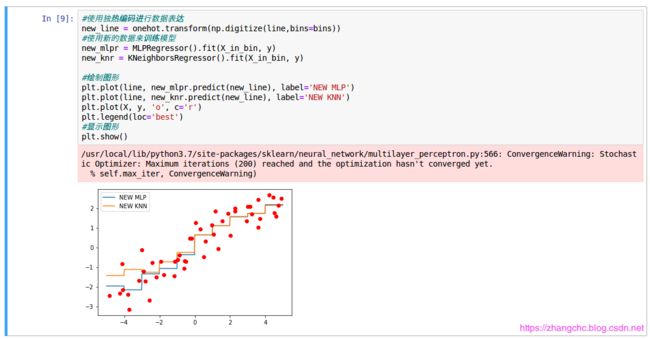
       从图中可以看出来，MLP 模型和 KNN 模型变得更相似了，尤其在 x>0 的部分，两个模型几乎完全重合。对比于之前的图，可以看出 MLP 的回归模型变得更加复杂，而 KNN 的模型变得更加简单。所以这是对样本特征进行装箱的一个好处：它可以纠正模型过拟合和欠拟合的问题。尤其是在当针对大规模高纬度的数据集使用线性模型的时候，装箱处理可以大幅度提高线性模型的预测准确率。
       注意：这种对于样本数据进行装箱的操作对于基于决策树的算法（如随机森林、梯度上升决策树，当然也包括决策树本身）没有太多的作用，因为这类算法本身就是不停在拆分样本的特征数据，所以不需要再使用装箱操作。

数据 “ 升维 ”

• 向数据集添加交互式特征

       在实际中常常会遇到数据集的特征不足的情况，解决这个问题需要对数据集的特征进行扩充。统计建模中常用的方法有交互式特征（Interaction Features）和多项式特征（Polynomial Features）。
       交互式特征是在原始数据特征中添加交互项，使特征数量增加。在 Python 中可以通过 Numpy 的 hstack 函数来对数据集添加交互项，如下：

       在上面图片中，我们先建立了一个数组 array_1,并赋值为一个 1 ~ 5 的列表，然后又建立了另一个数组 array_2，并赋值为一个 6 ~ 0 的列表之后我们使用 np.hstack 函数将两个数组堆叠到一起。形成了一个 10 维数组 array_3。假如 array_1 和 array_2 分别代表两个数据点的特征，那么 array_3 就是它们的交互特征。
       进一步观察对模型的影响：

       可以发现，数量仍是 50 个，而特征数量变成了 11.接着训练模型：

       对比可知，上图的模型是倾斜的而之前我们看到的都是水平状态。也就是说，添加了交互式特征之后，在每个数据所在的箱体中，MLP 模型增加了斜率。相比之下，现在的模型的复杂度有所提高。
       但是这样操作会让每个箱体中模型的斜率都是一样的，这并不是我们所期望的结果，我们所希望的是每个箱体有自己的截距和斜率。如下所示：

       可以发现，经过上述处理之后，新的数据集特征 X_multi 变成了每个样本有 20 个特征值的状态。试着打印出第一个样本，发现 20 个特征中大部分数值是 0，而在之前的 X_in_bin 中数值为 1 的特征，与原始数据中 X 的第一个特征值 -1.1522688 保留了下来。
       用处理过的数据集训练神经网络，看看有什么不同：

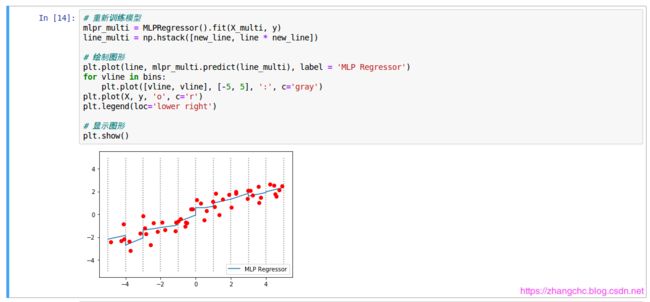
       分析发现，每个箱子中模型的 “ 截距 ” 和 “ 斜率 ” 都不一样了。而这种数据处理的目的，主要是为了让比较容易出现欠拟合现象的模型有更好的表现。例如，线性模型在高维数据集中有良好的性能，但是在低维数据集中却表现一般，因此可以使用上面的方法对特征进行扩充，以便给数据集 “ 升维 ”，从而提升线性模型的准确率。

• 向数据集添加多项式特征

       在机器学习当中，常用的多项式特征扩展方式就是将 x 进行乘方，如 $x^n$。在scikit-learn 中内置了一个功能，称为 PloynomialFeatures，使用这个功能可以轻松地将原始数据集的特征进行扩展。
       我们先是设定 PloynomialFeatures 的 degree 参数为 20， 这样可以生成 20 个特征。include_bias 设定为 False，如果设定为 True 的话，PloynomialFeatures 只会为数据添加数值为 1 的特征。可以看到下面的结果中样本仍是 50 个，但每个样本的特征数变成了 20 个。

       继续看看 PloynomialFeatures 对数据进行了什么样的调整，打印 1 个样本的特征：

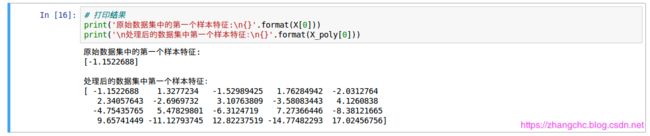
       从结果可以看出，原始数据集的样本只有一个特征，而处理后的数据集有 20 个特征。第一个特征就是原始数据样本特征，第二个特征就是原始数据特征的 2 次方，第三个特征是原始数据特征的 3 次方。继续用下面的程序验证一下:

       结果显示，PloynomialFeatures 是将原始数据样本进行了从 1 到 20 的乘方处理。下面看看处理后模型会发生什么变化：

        可以看出：对于低维数据集，线性模型经常会出现欠拟合的问题，而我们将数据集进行多项式特征扩展后，可以在一定程度上解决线性模型欠拟合的问题。

       在上述内容中，使用了一些对数据集特征进行扩展的方法，从而提升了线性模型或者是神经网络模型的回归分析性能，这种方法尤其在数据特征与目标呈现非线性关系时效果格外明显。当然，除了上面用到的 PolynomialFeatures 这种将特征值转化为多项式的方法之外，还可以使用类似正弦函数 sin()、对数函数 log(),或者是指数函数 exp() 等进行类似的操作。

自动特征选择

       在前面的分析中，介绍了如何对低维数据集扩充特征的方法。但是在复杂的特征当中，有一些对于模型预测结果的影响比较大，而有一些重要性相对较低，接下来介绍的就是使用 scikit-learn 进行自动特征选择。

• 使用单一变量法进行特征选择

       在进行统计分析的过程中，我们会选择那些置信度最高的样本特征来进行分析。当然这只适用于样本之间没有明显关联的情况，也就是单一变量法(univariate)。
       在scikit-learn 中，有若干种方法可以用来进行特征选择，其中最简单的两种就是SelectPercentile 和 SelectKBest ，其中 SelectPercentile 是自动选择原始特征的百分比，例如原始数据的特征数是 200 个，那么 SelectPercentile 的 percentile 参数设置为 50，就会选择 100 个原始特征中的 50%，即 100 个，而SelectKBest 是自动选择 K 个最重要的特征。
       下面是用 pandas 读取股票数据集：

       可以看出 csv 文件中包括 100 列分别对应代码、名称等信息。现在的目的是通过回归分析，预测股票的涨幅，因而 target 是 “ 涨幅 ” 这一列，如下：

       可以看到，数据集中一共有 3673 个样本，而第一个样本当日的涨幅为 -1.17%。这说明 target 指定成功。下面继续指定样本特征：

       可以看到，样本特征一共有 22 个，即从 “ 现价 ” 一直到 “ 流通股（亿）” 这一列。下面的数组是第一个样本的全部特征值，这里特征值之间的数量级差异比较大，从 e 的 -1 次方到 8 次方，这样的话，在训练模型之前，需要用 scikit-learn 的预处理模块进行一下数据缩放。如下：

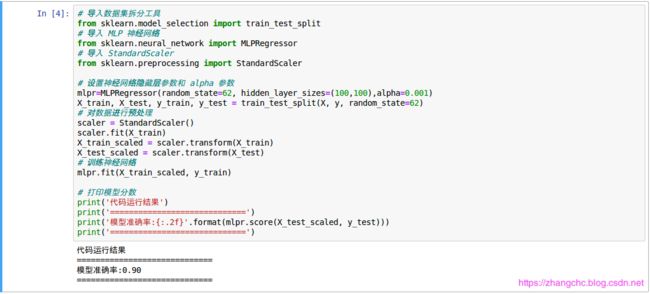
       可以看到，用神经网络对股票涨幅进行回归分析，模型的准确率达到了 90%，还不错。
       下面继续列出涨幅大于或等于 10% 的股票：

       股市有风险，投资需谨慎。上面的分析过程用的方法只是用来尝试对当日股票进行价格回归，不代表股票未来的价格变化，请勿以此作为投资建议。Carefully！！！
       下面指定 SelectPercentile 的百分比参数 precentile 为 50，即保留上一步缩放之后的数据的 50% 的特征：

       得到原始数据特征是 22 个，而经过特征选择之后只剩下 11 个。
       接着，可以用 get_support 方法来查看一下剩下的是哪些特征：

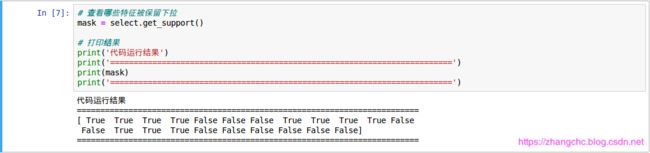
       在结果中，False 代表该特征没有被选择，Ture 代表特征被选中了，对照前面的特征名称，可以查看对应的特征。
       用图形显示特征选择结果如下：

       接着试试用特征选择后的数据集训练神经网络：

       从结果可以看出，模型得分有所降低。这也是正常的，因为我们的数据集中并不包括噪声。对于噪声特别多的数据集来说，进行特征选择后模型评分会提高，而不是降低。
       以上就是使用单一变量法进行特征选择的方法，这种方法不依赖于你用什么样的算法进行建模,也就是说无论哪一个模型，它对数据进行处理的方式都是一样的。

• 基于模型的特征选择

       基于模型的特征选择工作原理是，先使用一个监督学习的模型对数据特征的重要性进行判别，然后把最重要的特征进行保留。当然，这一步中用到的模型和最终用来进行预测分析的模型不一定是同一个。例如 SelectFromModel。
       下面是用 SelectFromModel 对股票数据集进行实验：

       在程序中用了随机森林回归模型来进行特征选择。这是因为包括随机森林在内的基于决策树的算法都会内置一个 feature_importances_ 的属性，我们可以让 SelectFromModel 直接从这个属性中抽取特征的重要性。除了随机森林之外，其它算法也可以，例如 L1正则化的线性模型，它们可以对数据空间的稀疏系数进行学习，从而可以当作特征重要性来抽取。原本这个系数是线性模型用来自己建模的，但我们可以借助它来帮助其它模型进行数据预处理。
       从程序运行的结果可以发现，通过基于随机森林模型进行特征选择之后，数据集的特征还剩 11 个。
       下面继续看看基于随机森林模型的特征选择有什么区别：

       这个时候保留了第 2、3、4、9、10、11、14、15、19、20、21 个特征。同样可以对其进行特征选择可视化：

       可以直观的看到基于随机森林模型进行的特征选择和使用单一变量法进行特征选择的区别。
       在进行特征选择时，使用了一个有 100 棵决策树的随机森林，这使得模型相当复杂，但是它会比单一变量法强悍很多。同时指定 threshold 参数，也就是 “ 阈值 ” 为 median 中位数，这意味着模型会选择一般左右的特征。下面便是经过随机森林模型选择的特征在实际训练模型中的表现：

       使用随机森林进行特征选择后，在其它参数都不变的情况下，模型的得分会比使用单一变量法进行特征选择的分数高一些，而且更加接近原始数据集的得分（有时可以超过它）。

• 迭代式特征选择

       迭代式特征选择是基于若干个模型进行特征选择。在scikit-learn 中，有一个称为递归特征剔除法（Recurise Feature Elimination，RFE）的功能就是通过这种方式来进行特征选择的。在最开始，RFE 会使用某个模型对特征进行选择，之后在建立两个模型，其中一个对已经被选择的特征进行筛选；另外一个对被剔除的模型进行筛选，然后一直重复这个步骤，直到达到我们指定的特征数量。这种方式比我们学习的基于单个模型进行特征选择更加强悍，但相应的是，对计算能力的要求也更高。
       下面这段程序时用 RFE 对股票数据集进行特征选择：

       从结果可以看出 RFE 筛选出的特征数量为 12 个，分别是第 2、3、4、9、10、11、、14、15、16、19、20、21 个特征。同样可视化一下：

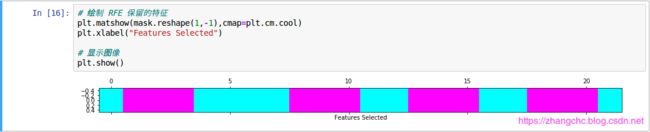
       可以看到 RFE 选择出的特征和前面的单一变量法以及基于单个模型的特征选择结果都不同，而下面更关注的是模型的得分。

       可以看出，使用 RFE 进行特征选择后模型的得分比使用原始数据集特征选择和单个模型选择的特征选择的得分都高。需要注意的是，不同的方法并没有绝对的好与不好，只是适用于不同的场景。
       
       
       
       
       
       
       小编机器学习学的一般，只是日常做做比记加深一下印象，望读者不吝赐教，谢谢！