斐波那契堆(Fibonacci heaps)

一：斐波那契堆

1：特性

斐波那契堆同二项堆一样,也是一种可合并堆。斐波那契堆的优势是：不涉及删除元素的操作仅需要O（1）的平摊运行时间（关于平摊分析的知识建议看《算法导论》第17章）。和二项堆一样，斐波那契堆由一组树构成。这种堆松散地基于二项堆，说松散是因为：如果不对斐波那契堆做任何DECREASE-KEY 或 DELETE 操作，则堆中每棵树就和二项树一样；但是如果执行这两种操作，在一些状态下必须要破坏二项树的特征，比如DECREASE-KEY或DELETE 后，有的树高为k，但是结点个数却少于2k。这种情况下，堆中的树不是二项树。
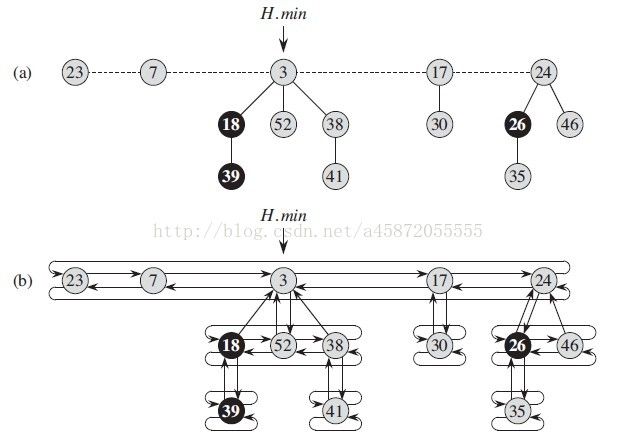
     与二项堆相比，斐波那契堆同样是由一组最小堆有序树构成。最小堆性质：每个结点的关键字大于等于父节点的关键字。但是斐波那契堆中的树都是有根而无序的，也就是说，单独的树满足最小堆特性，但是堆内树与树之间是无序的，如下图。
     对于斐波那契堆上的各种可合并操作，关键思想是尽可能久地将工作推后。例如，当向斐波那契堆中插入新结点、删除结点或合并两个斐波那契堆时，并不去合并树，而是将这个工作留给EXTRACT-MIN操作。

看一下斐波那契堆的链表结构表示：

2：每个结点的域：

//斐波那契结点ADT
struct FibonacciHeapNode {
    int key;       //结点
    int degree;    //度
    FibonacciHeapNode * left;  //左兄弟
    FibonacciHeapNode * right; //右兄弟
    FibonacciHeapNode * parent; //父结点
    FibonacciHeapNode * child;  //第一个孩子结点
    bool marked;           //是否被删除第1个孩子
};
typedef FibonacciHeapNode FibNode;

除了关键字key以外的结点信息：
1） 父节点*p
2） 指向任一子女的指针*child——结点x的子女被链接成一个环形双链表，称为x的子女表
3） 左兄弟*left
4） 右兄弟*right——当left[x] = right[x] = x时，说明x是独子。
5） 子女的个数degree[x]
6） 布尔值域mark[x]——标记是否失去了一个孩子

3：堆结构

对于一个给定的斐波那契堆H，可以通过指向包含最小关键字的树根的指针H.min来访问，这个结点被称为斐波那契堆中的最小结点。如果一个斐波那契堆H是空的，则H.min = NIL. 在一个斐波那契堆中，所有树的根都通过left和right指针链接成一个环形的双链表，称为堆的根表。于是，指针H.min就指向根表中具有最小关键字的结点。

指向根结点的堆结构体：

//斐波那契堆ADT
struct FibonacciHeap {
    int keyNum;   //堆中结点个数
    FibonacciHeapNode * min;//最小堆，根结点
    int maxNumOfDegree;   //最大度
    FibonacciHeapNode * * cons;//指向最大度的内存区域
};
 
typedef FibonacciHeap FibHeap;

二：操作的实现

1：创建一个斐波那契堆

创建一个空的斐波那契堆，过程MAKE-FIB-HEAP 分配并返回一个斐波那契堆对象H；

//初始化一个空的Fibonacci Heap，堆结点信息
FibHeap * FibHeapMake()
{
    FibHeap * heap = NULL;
    heap = (FibHeap *) malloc(sizeof(FibHeap));
    if (NULL == heap) {
        puts("Out of Space!!");
        exit(1);
    }
    memset(heap, 0, sizeof(FibHeap));
    return heap;
}
 
//初始化结点x
FibNode * FibHeapNodeMake()
{
    FibNode * x = NULL;
    x = (FibNode *) malloc(sizeof(FibNode));
    if (NULL == x) {
        puts("Out of Space!!");
        exit(1);
    }
    memset(x, 0, sizeof(FibNode));
    x->left = x->right = x;
    return x;
}

2：插入一个结点（仅将x结点插入到根链表中，不进行合并处理）

//函数调用前，结点x已经分配了空间，key已经被赋值
FIB-HEAP-INSERT(H, x)
  degree[x] ← 0    //初始化结点x的基本信息
  p[x] ← NIL
  child[x] ← NIL
  left[x] ← x
  right[x] ← x
  mark[x] ← FALSE
  if min[H] == NIL      //处理空树的情况
    creat a root list for H containing just x
    H.min = x
  else  insert x into H's root list
        if key[x] < key[min[H]]
            then min[H] ← x
  n[H] ← n[H] + 1

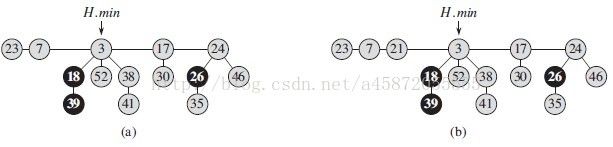
如图是将关键字为21的结点插入斐波那契堆。该结点自成一棵最小堆有序树，从而被加入到根表中，成为根的左兄弟。

3：合并两个斐波那契堆

仅仅简单地将H1和H2的两根表并置，然后确定一个新的最小结点。

伪代码：

FIB-HEAP-UNION(H1, H2)
{
    H ← MAKE-FIB-HEAP() //创建一个空的堆，用来存放H1,H2
    min[H] ← min[H1]
    concatenate the root list of H2 with the root list of H
    if (min[H1] = NIL) or (min[H2] ≠ NIL and min[H2] < min[H1]) //找到关键字最小的结点
        then min[H] ← min[H2]
    n[H] ← n[H1] + n[H2]    //堆元素的总个数
    free the objects H1 and H2  //这里h1、h2是指向根结点的堆结构体
    return H
}

最后要销毁H1、H2，并不是将原来的两个堆全销毁，只是销毁的是头结点信息。由于已经创建了H 结点，合并后的堆的信息存储在H中。

4：抽取最小结点

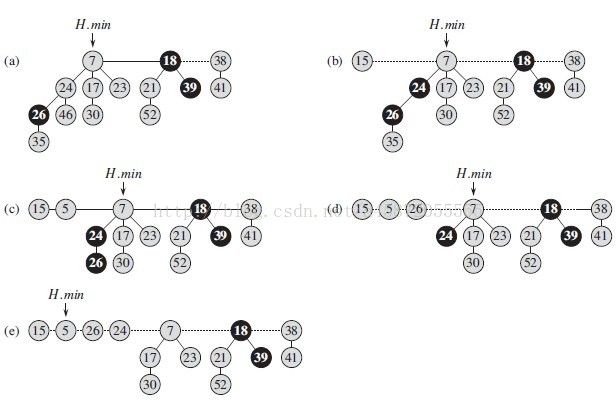
前边说过，对根表中的树合并是推后到EXTRACT-MIN中的，所以抽取最小这个操作比较麻烦。该过程还用到一个辅助过程CONSOLIDATE。

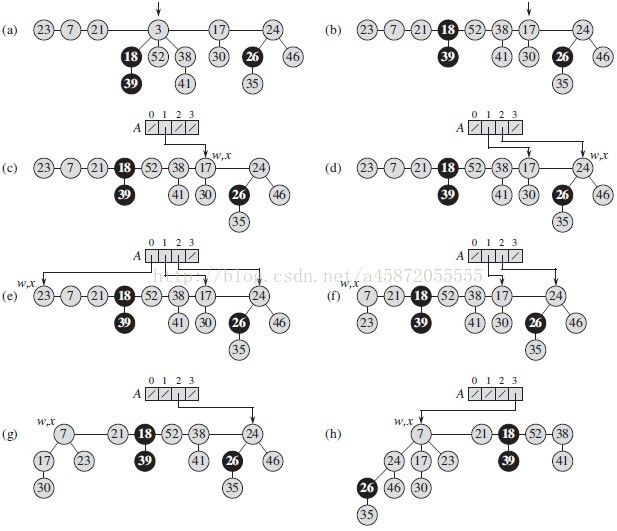
先上图，对整个变换过程有个了解

下面说一下EXTRACT-MIN过程的实现（上图中的a->b过程）

//取出最小值后，调整堆，并且满足根链表结点的度不相同
FIB-HEAP-EXTRACT-MIN(H)
{
    z ← min[H]      
    if z ≠ NIL  //如果z非空，则取出了最小值
        for each child x of z   //将z结点的孩子全部放入根链表当中
            add x to the root list of H
            p[x] ← NIL  //同时调整刚加入根链表结点的父指针信息
        remove z from the root list of H    //将孩子结点信息加入根链表以后，在新的链表中删除z，这时z已经没有孩子结点
        if z == right[z]     //如果二者相等，证明当前状态下，整个堆中只有z一个结点
            min[H] ← NIL
        else min[H] ← right[z]  //如果z不是唯一结点，则随便将根链表中的结点当成临时的最小值
            CONSOLIDATE(H)      //调整堆结构，并求得最小值
        n[H] ← n[H] – 1 //调整信息
    return z
}

评注：这里只做了三件事：将z结点的孩子结点放入根链表，移除z结点（只是移除，z结点的指针依然不变化），h.min指向根链表某一个结点。

主要任务还是要在CONSOLIDATE()中来实现

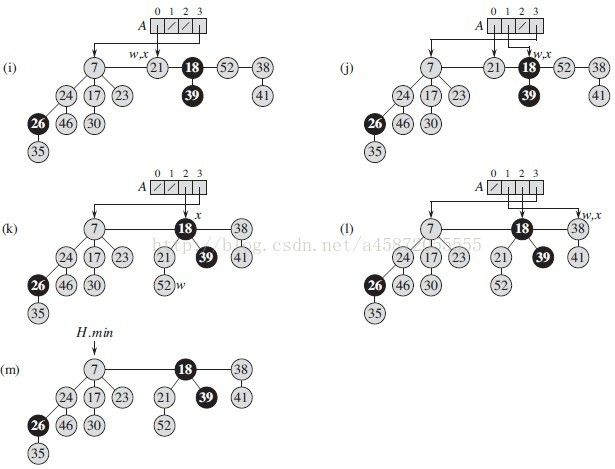
CONSOLIDATE过程要做的工作是：使每个度数的二项树唯一，也就是使每个根都有一个不同的degree值为止。对根表的合并过程是反复执行下面的步骤：
1）在根表中找出两个具有相同度数的根x和y，且key[x] <= key[y].（如果不满足，则交换，保持key[x]<=key[y]）
2)将y链接到x：将y从根表中移出，成为x的一个孩子。这个过程由FIB-HEAP-LINK完成。

这个过程中使用一个辅助数组指针A[0...D(H.n)]来记录根结点对应的度数的信息，指向度数为i的结点。比如，当遍历到某一结点x时，这个结点的度数为d，那么判断A[d]是否为空，不为空，证明具有相同的度数d，将当前结点x和A[d]指向的结点y合并；然后将x度数递增1，然后递归进行与A[d+1]的判断。

CONSOLIDATE(H)
1 for i ← 0 to D(n[H])  //初始化数组A[]
2      do A[i] ← NIL
3 for each node w in the root list of H
4      do x ← w
5         d ← degree[x]
6         while A[d] ≠ NIL
7             do y ← A[d]     //Another node with the same degree as x.
8                if key[x] > key[y] //保持key[x] <= key[y]
9                   then exchange x ↔ y
10                FIB-HEAP-LINK(H, y, x)    //将y变为x的子节点
11                A[d] ← NIL    //必须更新A[d]
12                d ← d + 1
13         A[d] ← x
14 min[H] ← NIL
15 for i ← 0 to D(n[H])     //遍历整个数组，将根结点插入到根链表当中。这里重新创建根链表
16      do if A[i] == NIL
17            then create a root list for H containing just A[i]
18                 min[H] ← A[i]
19         else insert A[i] into H's root list
20               if key[A[i]] < key[min[H]]
21                    then min[H] ← A[i]

FIB-HEAP-LINK(H, y, x)
1  remove y from the root list of H
2  make y a child of x, incrementing degree[x]
3  mark[y] ← FALSE

5：关键字减小

减小关键字操作最大的难点是，如果减小后的结点破坏了最小堆的性质，如何维护斐波那契堆的性质。这里用到一个操作：级联剪枝（Cascading Cut）。减小关键字的代码流程基本就是：如果减小后的结点破坏了最小堆性质，则把它切下来(cut)，即从所在双向链表中删除，并将其插入到由最小树根节点形成的双向链表中，然后再从parent[x]到所在树根节点递归执行级联剪枝。

关于级联剪枝，《数据结构》中的解释：
由于增加了删除和关键字减值操作，所以，F堆中的最小树就不一定必须是二项树了。事实上，可能存在度为k却只有k + 1（原书是k + 1，应该是k – 1吧）个结点的最小树。为了保证每个度为k的最小树至少包含ck个结点（c > 1)， 每次执行删除操作和关键字减值操作后，还必须进行级联剪枝操作。为此，为每个结点增加一个布尔类型的child_cut域（即本文里的marked)。child_cut域的值仅对那些不是最小树树根的结点有意义。对于不是最小树树根的结点x， x的child_cut域为TRUE，当且仅当在最近一次x成为其当前父结点的儿子之后，x的一个儿子被删除。这就意味着，在执行删除最小元素中，每次连接两棵最小树时，关键字值较大的根结点的child_cut域应该赋值为FALSE。更进一步地说，一旦删除操作或关键字减值操作将最小树的非根结点q从其所在双向链表中删除时，则调用级联剪枝操作。在执行级联剪枝操作过程中，检查从被删除结点q的父节点p开始，到被删节点的最近的child_cut域为FALSE的祖先结点的路径。对在该路径上所有child_cut域为TRUE的非根结点，将其从所在的双向链表中删除，并将其加入到F堆的最小树的根节点组成的双向链表中。如果该路径上存在child_cut域为FALSE的结点 ,则将其该域的值修改为TRUE。

伪代码

FIB-HEAP-DECREASE-KEY(H, x, k)
1  if k > key[x]    //保证值是减小的
2     then error "new key is greater than current key"
3  key[x] ← k
4  y ← p[x] 
5  if y ≠ NIL and key[x] < key[y]   //与父节点相比较，如果比父节点小，进入循环
6     then CUT(H, x, y)             //将x从y中移除，并放到根链表中，当然，x的孩子也要随着x一起走，
7          CASCADING-CUT(H, y)      //级联剪切判断，判断非根结点y是否失去的是第二个孩子。
8  if key[x] < key[min[H]]
9      then min[H] ← x


CUT(H, x, y)
1 remove x from the child list of y, decrementing degree[y]
2 add x to the root list of H
3 p[x] ← NIL
4 mark[x] ← FALSE

//当y不是根结点时，失去第一个孩子时，标记为true，失去第二个孩子时，将y移除放入根链表，递归处理y的父节点。
CASCADING-CUT(H, y)
1 z ← p[y]
2 if z ≠ NIL
3    then if mark[y] = FALSE
4            then mark[y] ← TRUE
5            else CUT(H, y, z)
6                 CASCADING-CUT(H, z)

图形实例：

级联剪切的过程很明了，我当时看的时候最烦的问题是，为什么要进行级联剪切，级联剪切丫的要干什么？ 
     如果仅仅要切除父结点y的一个结点x，则仅仅需要把结点x加入到根结点所在双向链表中，再检测y是否marked == true即可，这是因为斐波那契中的树并不一定是二项树，近似二项树也可以。当删除y的第二个结点时，对在该路径上所有marked域为TRUE的非根结点，将其从所在的双向链表中删除，并将其加入到F堆的最小树的根节点组成的双向链表中，即只有在删除同一个结点偶数个孩子时，才要进行级联剪枝，来维护二项树性质，奇数个时（即一个），对树影响不大，莫管它，只标记一下即可。
为什么偶数个的时候要递归往上删除？
     二项树中在深度为i处恰有Cik个结点(I = 0, 1, 2, ……, k)。试着如果不进行级联剪枝，就可以发现，稍微删得结点超过两三个，最后的树就会不成样子，毫无章法。但是如果进行了级联剪枝，在偶数个结点时进行级联剪切时，原来是C30 = 1, C31 = 3, C32 = 3, C33 = 1, 减少两个结点关键字后，变为：C20 = 0，C21 = 2， C22 = 1;二项式是对称的，所以，偶数个结点时进行级联剪枝可以保证类似上边的正好使二项式减少一个数量级。

八、删除一个结点
伪代码：
FIB-HEAP-DELETE(H, x)
1 FIB-HEAP-DECREASE-KEY(H, x, -∞)
2 FIB-HEAP-EXTRACT-MIN(H)
过程很简单，先减小直到min[H], 然后直接剔除最小值即可

详细代码：斐波那契堆实现文件C语言

参考：斐波那契堆(Fibonacci heaps)