吴恩达机器学习学习笔记（四）（附作业代码注释）

吴恩达机器学习学习笔记（四）

标签： 机器学习

---

代价函数与反向传播（Costfunction and Backpropagation）

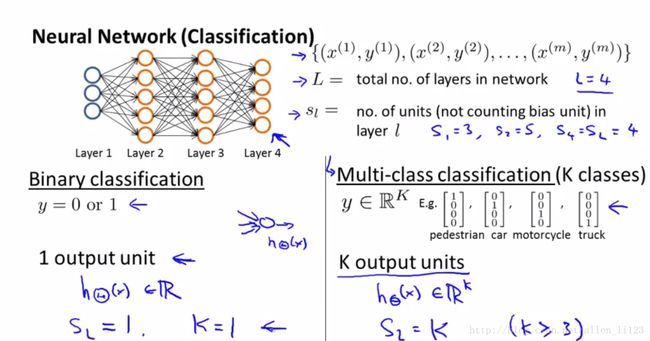
一.代价函数

L：代表神经网络的层数
s_l sl 代表第i层的单元数
k代表输出层的单元数
二元分类问题时：
y=0 或者 y=1
仅有一个输出，s_l sl =1
k=0
当多元分类k=0问题时：
s_l sl =k(当k>=3)
y为一个K维矩阵，有k个输出单元

1逻辑分类的评价函数：

J(\theta) = - \frac{1}{m} \sum_{i=1}^m [ y^{(i)}\ \log (h_\theta (x^{(i)})) + (1 - y^{(i)})\ \log (1 - h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2

J(θ)=−1m∑i=1m[y(i) log(hθ(x(i)))+(1−y(i)) log(1−hθ(x(i)))]+λ2m∑j=1nθ2j

2.神经网络的评价函数：

J(Θ)=−1m∑i=1m∑k=1K[y(i)klog((hΘ(x(i)))k)+(1−y(i)k)log(1−(hΘ(x(i)))k)]+λ2m∑l=1L−1∑i=1sl∑j=1sl+1(Θ(l)j,i)2

2.1note:

1.这两项简单相加就可以计算出输出层中每个单元的逻辑回归成本。
2.三重平方和简单地加起来的是所有 θs 整个神经网络的 θ 。
2.三重平方和中的i不指训练样本i。

3.反向传播

训练集： {(x(1),y(1))⋯(x(m),y(m))}
令 Δ(l)i,j =0

for i in range m：
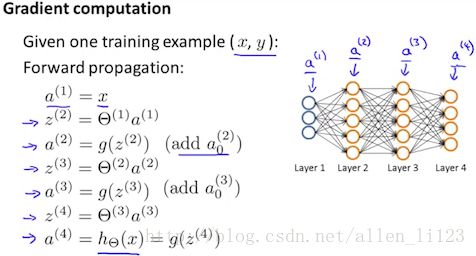
1. a(1):=x(t)
2.使用正向传播计算出所有的 a(l)
3.用 y(t) 计算出 δ(L)=a(L)−y(t)
4.计算出 δ(L−1),δ(L−2),…,δ(2) 其中\delta^{(l)} = ((\Theta^{(l)})^T \delta^{(l+1)})\ .*\ a^{(l)}\ .*\ (1 - a^{(l)}) δ(l)=((Θ(l))Tδ(l+1)) .∗ a(l) .∗ (1−a(l))
note: g′(z(l))=a(l) .∗ (1−a(l))
5.

Δ(l)i,j:=Δ(l)i,j+a(l)jδ(l+1)i

向量形式：

Δ(l):=Δ(l)+δ(l+1)(a(l))T

总偏导数:

D(l)i,j:=1m(Δ(l)i,j+λΘ(l)i,j)(if j≠0)

D(l)i,j:=1mΔ(l)i,j(If j=0)

note：正向传播

二.反向传播应用

2.1参数展开（Unrolling Parameters)

当调用优化算法时是传入一个长向量thetaVe而不是theta1,theta2,theta3等等
所以将theta1,theta2,theta3放入一个长向量thetaVe
执行thetaVec=[theta1(:);theta1(:)；theta1(:)];
但是我们使用costfunction函数时传入thetaVec需要将其展开为theta1,theta2,theta3
执行：theta1=reshape（thetaVec（1：110），10，11）；

2.2梯度检测（Gradient Checking)

对于单个参数而言

∂∂ΘJ(Θ)≈J(Θ+ϵ)−J(Θ−ϵ)2ϵ

递推到多个参数：

∂∂ΘjJ(Θ)≈J(Θ1,…,Θj+ϵ,…,Θn)−J(Θ1,…,Θj−ϵ,…,Θn)2ϵ

代码实现：

epsilon = 1e-4;
for i = 1:n,
  thetaPlus = theta;
  thetaPlus(i) += epsilon;
  thetaMinus = theta;
  thetaMinus(i) -= epsilon;
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;

运算完成后检查是否gradApprox ≈ deltaVector

2.3随机初始化（Random Initialization）

确保初始化的 θ 的范围在 [−ϵ,ϵ] 之间

代码实现：

If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.

Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

三.总结

如何实现神经网络的步骤

• 确定神经网络的输入单元个数（$x^{( 确定
• 确定输出层的单元个数（分类个数）
• 确定每个隐藏层的单元个数（越多越好，但是会导致运算量很大）
• 如果有一个以上的隐藏层，则默认每个隐藏层的单元数一样

确认神经网络后训练神经网络
1. 随机初始化权重
2. 使用前向传播对每一个 x(i) 获得其 hΘ(x(i))
3. 实现代价函数
4. 实现反向传播计算偏导数
5. 使用梯度检测检查反向传播是否正常工作，然后关闭梯度检测.
6. 使用梯度下降或者其他优化函数，使代价函数最小化

执行正向传播或者反向传播时，对每一个训练样本进行循环

for i = 1:m,
   Perform forward propagation and backpropagation using example (x(i),y(i))
   (Get activations a(l) and delta terms d(l) for l = 2,...,L

四.作业代码实现

1. nnCostFunction.m

%给输入层添加偏置单元

X = [ones(m, 1) X];                    
ylabel = zeros(num_labels, m);         %把y变成一个矩阵
for i=1:m
    ylabel(y(i), i) = 1;
end

%正向传播实现代码

z2 = X*Theta1';                  
z2 = [ones(m, 1) z2];
a2 = sigmoid(X*Theta1');
a2 = [ones(m, 1) a2];
a3 = sigmoid(a2*Theta2');

%不含正则化的代价函数代码实现

for i=1:m                         
    J = J - log(a3(i, :))*ylabel(:, i) - (log(1 - a3(i, :)) * (1 - ylabel(:, i)));
end
J = J/m;

%为代价函数添加正则化                                  

J = J + lambda/2/m * (sum(sum(Theta1(:, 2:end).^2)) + sum(sum(Theta2(:, 2:end).^2)));


Delta1 = zeros(size(Theta1));         %初始化偏差值       
Delta2 = zeros(size(Theta2));

%反向传播代码实现

for t = 1:m                           
    delta3 = a3(t, :)' - ylabel(:, t);
    delta2 = Theta2'*delta3 .* sigmoidGradient(z2(t, :)');

    Delta1 = Delta1 + delta2(2:end) * X(t, :);
    Delta2 = Delta2 + delta3 * a2(t, :);
end

%求偏导数代码实现
Theta1_grad = Delta1 / m;
Theta1_grad(:, 2:end) = Theta1_grad(:, 2:end) + lambda/m*Theta1(:, 2:end);
Theta2_grad = Delta2 / m;
Theta2_grad(:, 2:end) = Theta2_grad(:, 2:end) + lambda/m*Theta2(:, 2:end);

2.sigmoidGradient.m.

g = sigmoid(z).*(1 - sigmoid(z));   %求S型函数的偏导数

3.randInitializeWeights.m

%(L_out, 1 + L_in) 是需要生成的初始化权重矩阵，范围在[-epsilon,+epsilon]
epsilon = 0.12;
W = rand(L_out, 1+L_in)*2*epsilon - epsilon;