椭圆曲线密码原理
椭圆曲线密码概述
⾃从公钥加密被发明之后,⼀些合适的数学函数被提出,譬如:素数幂和椭圆曲线乘法。这些数学函数都是不可逆的,就是说很容易向⼀个⽅向计算,但不可以向相反⽅向倒推。基于这些数学函数的密码学,使得⽣成数字密钥和不可伪造的数字签名成为可能。
⽐特币正是使⽤椭圆曲线乘法作为其公钥加密的基础算法。
在⽐特币系统中,我们⽤公钥加密创建⼀个密钥对,⽤于控制⽐特币的获取。密钥对包括⼀个私钥,和由其衍⽣出的唯⼀的公钥。公钥⽤于接收⽐特币,⽽私钥⽤于⽐特币⽀付时的交易签名。
公钥和私钥之间的数学关系,使得私钥可⽤于⽣成特定消息的签名。此签名可以在不泄露私钥的同时对公钥进⾏验证。
⽀付⽐特币时,⽐特币的当前所有者需要在交易中提交其公钥和签名(每次交易的签名都不同,但均从同⼀个私钥⽣成)。⽐特币⽹络中的所有⼈都可以通过所提交的公钥和签名进⾏验证,并确认该交易是否有效,即确认⽀付者在该时刻对所交易的⽐特币拥有所有权。
通过椭圆曲线算法可以从私钥计算得到公钥, 这是不可逆转的过程: K = k * G 。 其中 k 是私钥, G 是被称为⽣成点的常数
点, ⽽ K 是所得公钥。 其反向运算, 被称为“寻找离散对数”——已知公钥 K 来求出私钥 k ——是⾮常困难的, 就像去试验所
有可能的 k 值, 即暴⼒搜索。 在演⽰如何从私钥⽣成公钥之前, 我们先稍微详细学习下椭圆曲线加密学。
椭圆曲线密码原理
椭圆曲线加密法是⼀种基于离散对数问题的⾮对称(或公钥) 加密法, 可以⽤对椭圆曲线上的点进⾏加法或乘法运算来表达。
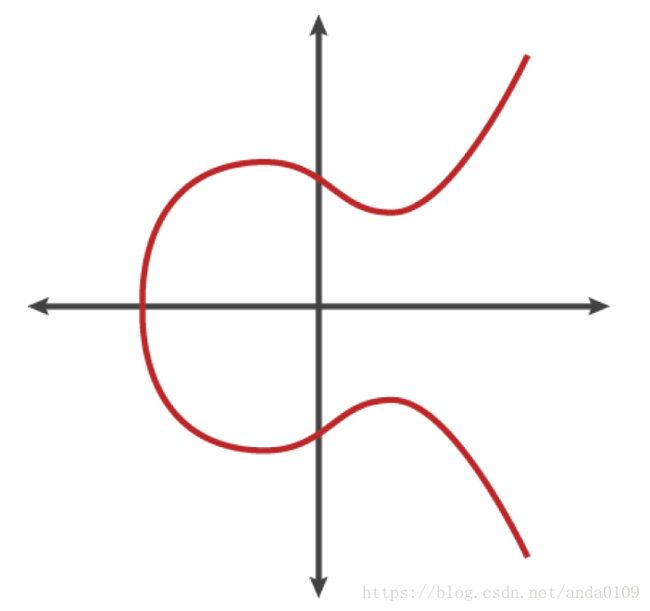
上图是⼀个椭圆曲线的⽰例, 类似于⽐特币所⽤的曲线。
⽐特币使⽤了 secp256k1 标准所定义的⼀条特殊的椭圆曲线和⼀系列数学常数。 该标准由美国国家标准与技术研究院(NIST) 设⽴。 secp256k1 曲线由下述函数定义, 该函数可产⽣⼀条椭圆曲线:
y^2 = (x^3 + 7) over (Fp)
或
y^2 mod p = (x^3 + 7) mod p
上述mod p(素数p取模) 表明该曲线是在素数阶p的有限域内, 也写作Fp, 其中p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1,这是⼀个⾮常⼤的素数。
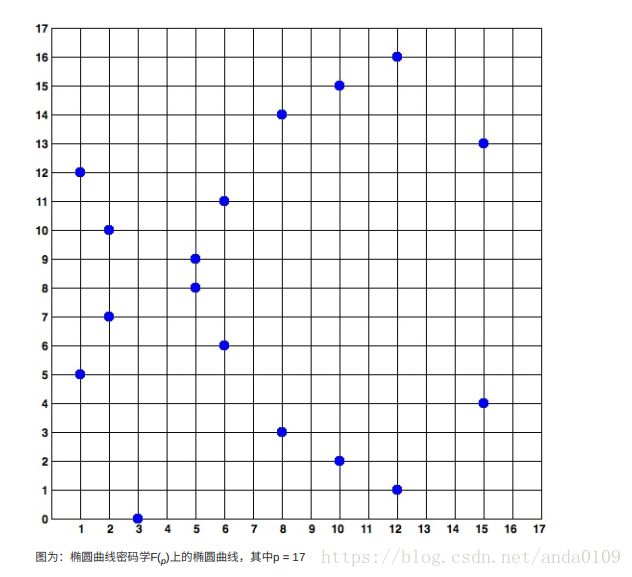
因为这条曲线被定义在⼀个素数阶的有限域内, ⽽不是定义在实数范围, 它的函数图像看起来像分散在两个维度上的散点图, 因此很难画图表⽰。 不过, 其中的数学原理与实数范围的椭圆曲线相似。 作为⼀个例⼦, 下图显⽰了在⼀个⼩了很多的素数阶17的有限域内的椭圆曲线, 其形式为⽹格上的⼀系列散点。 ⽽secp256k1 的⽐特币椭圆曲线可以被想象成⼀个极⼤的⽹格上⼀系列更为复杂的散点。
下⾯举⼀个例⼦, 这是 secp256k1 曲线上的点P, 其坐标为(x, y)。 可以使⽤Python对其检验:
P =(55066263022277343669578718895168534326250603453777594175500187360389116729240,326705100207588169780830851305070431844712733806592432759389043
Python 3.4.0 (default, Mar 30 2014, 19:23:13)
[GCC 4.2.1 Compatible Apple LLVM 5.1 (clang-503.0.38)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
>>> x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
>>> y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
>>> (x ** 3 + 7 - y**2) % 在椭圆曲线的数学原理中, 有⼀个点被称为“⽆穷远点”, 这⼤致对应于0在加法中的作⽤。 计算机中, 它有时表⽰为X = Y =0(虽然这不满⾜椭圆曲线⽅程, 但可作为特殊情况进⾏检验) 。 还有⼀个 + 运算符, 被称为“加法”, 就像⼩学数学中的实数相加。 给定椭圆曲线上的两个点P1和P2, 则椭圆曲线上必定有第三点 P3 = P1 + P2。
⼏何图形中, 该第三点P3可以在P1和P2之间画⼀条线来确定。 这条直线恰好与椭圆曲线上的⼀点相交。 此点记为 P3’=(x, y)。 然后, 在x轴做映射获得 P3=(x, -y)。
下⾯是⼏个可以解释“⽆穷远点”之存在需要的特殊情况。 若 P1和 P2是同⼀点, P1和P2间的连线则为点P1 的切线。 曲线上有且只有⼀个新的点与该切线相交。 该切线的斜率可⽤微分求得。 即使限制曲线点为两个整数坐标也可求得斜率!
在某些情况下(即, 如果P1和P2具有相同的x值, 但不同的y值) , 则切线会完全垂直, 在这种情况下, P3 = “⽆穷远点”。若P1就是“⽆穷远点”, 那么其和 P1 + P2= P2。 类似地, 当P2是⽆穷远点, 则P1+ P2 = P1。 这就是把⽆穷远点类似于0的作⽤。
事实证明, 在这⾥ + 运算符遵守结合律, 这意味着(A+B)C = A(B+C)。 这就是说我们可以直接不加括号书写 A + B + C, ⽽不⾄于混淆。
⾄此, 我们已经定义了椭圆加法, 为扩展加法下⾯我们对乘法进⾏标准定义。 给定椭圆曲线上的点P, 如果k是整数, 则 kP = P + P + P + …+ P(k次) 。 注意, k被有时被混淆⽽称为“指数”。
生成公钥
以⼀个随机⽣成的私钥k为起点, 我们将其与曲线上已定义的 ⽣成点G相乘以获得曲线上的另⼀点, 也就是相应的公钥K。 ⽣成点是secp256k1标准的⼀部分, ⽐特币密钥的⽣成点都是相同的:
{K = k * G}其中k是私钥, G是⽣成点, 在该曲线上所得的点K是公钥。 因为所有⽐特币⽤⼾的⽣成点是相同的, ⼀个私钥k乘以G将得到相同的公钥K。 k和K之间的关系是固定的, 但只能单向运算, 即从k得到K。 这就是可以把⽐特币地址(K的衍⽣) 与任何⼈共享⽽不会泄露私钥(k) 的原因。
为实现椭圆曲线乘法,我们以之前产⽣的私钥k和与⽣成点G相乘得到公钥K:
K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD * G公钥K 被定义为⼀个点 K = (x, y):
x = F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
y = 07CF33DA18BD734C600B96A72BBC4749D5141C90EC8AC328AE52DDFE2E505BDB为了展⽰整数点的乘法,我们将使⽤较为简单的实数范围的椭圆曲线。请记住,其中的数学原理是相同的。我们的⽬标是找到⽣成点G的倍数kG。也就是将G相加k次。在椭圆曲线中,点的相加等同于从该点画切线找到与曲线相交的另⼀点,然后映射到x轴。

上图显⽰了在曲线上得到 G、2G、4G 、8G的⼏何操作。