深度学习(二十九)——Normalization进阶, CTC
Normalization进阶
和Batch Normalization类似的概念还有Weight Normalization和Layer Normalization。
Batch Normalization
从上图可以看出,BN是对input tensor的每个通道进行mini-batch级别的Normalization。而LN则是对所有通道的input tensor进行Normalization。
BN的特点:
对于batch size比较小的时候,效果非常不好,而batch size越大,那么效果则越好,因为其本质上是要通过mini-batch得到对整个数据集的无偏估计;
在训练阶段和推理阶段的计算过程是不一样的;
在CNN上表现较好,而不适用于RNN甚至LSTM。
Layer Normalization
LN的特点:
不依赖于batch size的大小,即使对于batch size为1的在线学习,也可以完美适应;
训练阶段和推理阶段的计算过程完全一样。
适用于RNN或LSTM,而在CNN上表现一般。
Weight Normalization
WN的公式如下:
w = g ∥ v ∥ v w=\frac{g}{\|v\|}v w=∥v∥gv
WN将权重分为模和方向两个分量,并分别进行训练。
论文:
《Weight Normalization: A Simple Reparameterization to Accelerate Training of Deep Neural Networks》
WN的特点:
计算简单,易于理解。
相比于其他两种方法,其训练起来不太稳定,非常依赖于输入数据的分布。
Cosine Normalization
Normalization还能怎么做?
我们再来看看神经元的经典变换 f w ( x ) = w ⋅ x f_w(x)=w\cdot x fw(x)=w⋅x。
对输入数据x的变换已经做过了,横着来是LN,纵着来是BN。
对模型参数w的变换也已经做过了,就是WN。
好像没啥可做的了。然而天才的研究员们盯上了中间的那个点,对,就是 ⋅ \cdot ⋅。
f w ( x ) = cos θ = w ⋅ x ∥ w ∥ ⋅ ∥ x ∥ f_w(x)=\cos \theta=\frac{w\cdot x}{\|w\|\cdot\|x\|} fw(x)=cosθ=∥w∥⋅∥x∥w⋅x
参考:
https://mp.weixin.qq.com/s/EBRYlCoj9rwf0NQY0B4nhQ
Layer Normalization原理及其TensorFlow实现
http://mlexplained.com/2018/01/10/an-intuitive-explanation-of-why-batch-normalization-really-works-normalization-in-deep-learning-part-1/
An Intuitive Explanation of Why Batch Normalization Really Works
http://mlexplained.com/2018/01/13/weight-normalization-and-layer-normalization-explained-normalization-in-deep-learning-part-2/
Weight Normalization and Layer Normalization Explained
https://mp.weixin.qq.com/s/KnmQTKneSimuOGqGSPy58w
详解深度学习中的Normalization,不只是BN(1)
https://mp.weixin.qq.com/s/nSQvjBRMaBeoOjdHbyrbuw
详解深度学习中的Normalization,不只是BN(2)
CTC
概述
Connectionist Temporal Classification,是一种改进的RNN模型。它主要解决的是时序模型中,输入数大于输出数,输入输出如何对齐的问题。它由Alex Graves于2006年提出。
论文:
《Connectionist Temporal Classification: Labelling Unsegmented
Sequence Data with Recurrent Neural Networks》
Alex Graves,瑞士IDSIA研究所博士,DeepMind研究员。
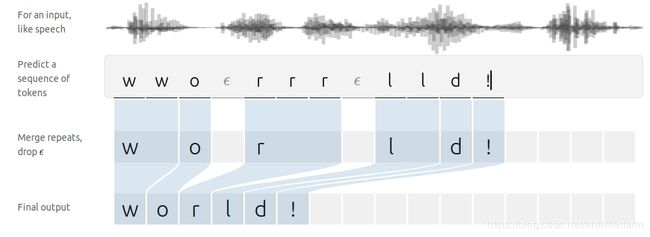
上图展示了音频数据被识别的过程:
1.将音频数据均分成若干段,每段匹配一个音节。
2.合并重复的音节,并去掉分割音节(即上图中的 ϵ \epsilon ϵ)。
相比于图像识别,人类语音的音节种类要少的多。但麻烦的是,一个音节的长短,会由于语速等因素的改变,而有较大差异。因此如何将数据段和音节匹配,成为了语音识别的难点。
这个问题不只是在语音识别中出现,我们在其他许多地方也能看到它。比如手写体识别、视频行为标注等。
我们首先用数学的方式定义对齐问题。假设输入序列为 X = [ x 1 , x 2 , … , x T ] X=[x_1,x_2,\dots,x_T] X=[x1,x2,…,xT],输出序列为 Y = [ y 1 , y 2 , … , y U ] Y=[y_1,y_2,\dots,y_U] Y=[y1,y2,…,yU],所谓对齐问题就是将X映射到Y。
这里的主要问题在于:
1.X和Y的长度可以变。
2.X和Y的长度比例可变。
3.我们没有一个X和Y之间的准确的对齐(对应元素)。
CTC算法可以克服这些挑战。对于一个给定的X,它给我们一个所有可能Y值的输出分布。我们可以使用这个分布来推断可能的输出或者评估一个给定输出的概率。
并不是所有的计算损失函数和执行推理的方法都是易于处理的。我们要求CTC可以有效地做到这两点。
损失函数:对于给定的输入,我们希望训练模型来最大化分配到正确答案的概率。 为此,我们需要有效地计算条件概率 p ( Y ∣ X ) p(Y \mid X) p(Y∣X)。 函数 p ( Y ∣ X ) p(Y \mid X) p(Y∣X)也应该是可微的,可以使用梯度下降。
推理:在我们训练好模型后,我们希望使用它来推断给定X的最可能的Y。即:
Y ∗ = argmax Y p ( Y ∣ X ) Y^*=\mathop{\text{argmax}}_{Y} p(Y \mid X) Y∗=argmaxYp(Y∣X)
算法推导
为了推导CTC对齐的具体形式,我们首先考虑一种初级的做法:假设输入长度为6,Y=[c,a,t],对齐X和Y的一种方法是将输出字符分配给每个输入步骤并折叠重复的部分。
这种方法存在两个问题:
1.通常,强制每个输入步骤与某些输出对齐是没有意义的。例如在语音识别中,输入可以具有无声的延伸,但没有相应的输出。
2.我们没有办法产生连续多个字符的输出。考虑这个对齐[h,h,e,l,l,l,o],折叠重复将产生“helo”而不是“hello”。
为了解决这些问题,CTC为一组允许的输出引入了一个新的标记。这个新的标记有时被称为空白标记。我们在这里将其称为 ϵ \epsilon ϵ , , , ϵ \epsilon ϵ标记不对应任何东西,可以从输出中移除。
CTC允许的对齐是与输入的长度相同。 在合并重复并移除 ϵ \epsilon ϵ标记后,我们允许任何映射到Y的对齐方式。
如果Y在同一行中有两个相同的字符,那么一个有效的对齐必须在它们之间有一个 ϵ \epsilon ϵ。有了这个规则,我们就可以区分“hello”和“helo”了。
CTC对齐有一些显著的特性:
首先,X和Y之间允许的对齐是单调的。如果我们前进到下一个输入,我们可以保持相应的输出相同或前进到下一个输入。
第二个属性是X到Y的对齐是多对一的。一个或多个输入元素可以对齐到一个输出元素,但反过来不成立。
这意味着第三个属性:Y的长度不能大于X的长度。
上图是CTC对齐的一般步骤:
1.输入序列(如音频的频谱图)导入一个RNN模型。
2.RNN给出每个time step所对应的音节的概率 p t ( a ∣ X ) p_t(a \mid X) pt(a∣X)。上图中音节的颜色越深,其概率p越高。
3.计算各种时序组合的概率,给出整个序列的概率。
4.合并重复并移除空白之后,得到最终的Y。
严格的说,一对(X,Y)的CTC目标函数是:
p ( Y ∣ X ) = ∑ A ∈ A X , Y ∏ t = 1 T p t ( a t ∣ X ) p(Y\mid X)=\sum_{A\in A_{X,Y}}\prod_{t=1}^Tp_t(a_t\mid X) p(Y∣X)=A∈AX,Y∑t=1∏Tpt(at∣X)
这里的模型通常使用一个RNN来估计每个time step的概率,但是也可以自由使用任何学习算法,在给定一个固定尺寸输入片段的情况下产生一个输出类别的分布。
在实际训练中,针对训练集 D \mathcal{D} D,一般采用最小化log-likelihood的方式计算CTC loss:
∑ ( X , Y ) ∈ D − log p ( Y ∣ X ) \sum_{(X,Y)\in \mathcal{D}}-\log p(Y\mid X) (X,Y)∈D∑−logp(Y∣X)
采用穷举法计算上述目标函数,计算量是非常巨大的。我们可以使用动态规划算法更快的计算loss。关键点是,如果两个对齐在同一步已经达到了相同的输出,可以合并它们。如下图所示:
这里如果把音节匹配换成掷骰子的例子,就可以看出这实际上和《机器学习(二十二)》中HMM所解决的第二个问题是类似的,而HMM的前向计算正是一种动态规划算法。动态规划算法可参见《机器学习(二十七)》。
下面我们来介绍一下具体的计算方法。
首先使用 ϵ \epsilon ϵ分隔Y中的符号,就得到了序列Z:
Z = [ ϵ , y 1 , ϵ , y 2 , … , ϵ , y U , ϵ ] Z=[\epsilon,y_1,\epsilon,y_2,\dots,\epsilon,y_U,\epsilon] Z=[ϵ,y1,ϵ,y2,…,ϵ,yU,ϵ]
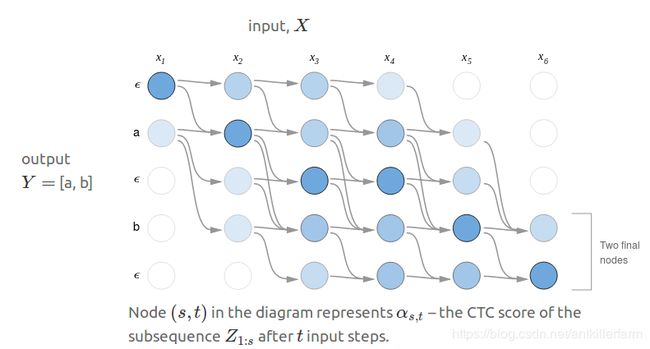
用 α s , t \alpha_{s,t} αs,t表示子序列 Z 1 : s Z_{1:s} Z1:s在t步之后的CTC值。显然,我们需要计算的目标 P ( Y ∣ X ) P(Y\mid X) P(Y∣X)和最后一步的 α \alpha α有关,但只有计算出了上一步的 α \alpha α,我们才能计算当前的 α \alpha α。
不同于掷骰子过程中,骰子的每种状态都有可能出现的情况,语音由于具有连续性,因此有些情况实际上是不可能的。比如上图的 x 1 x_1 x1就不大可能是后三个符号。
所以,可能的情况实际上只有两种:
Case 1
上图表示的是语音在两个相同token之间切换的情况。(这种情况也就是上面提到的hello例子中,语音在两个l之间过渡的情况。)
在这种情况下, α \alpha α的计算公式如下:
α s , t = ( α s − 1 , t − 1 + α s , t − 1 ) ⋅ p t ( Z s ∣ X ) \alpha_{s,t}=(\alpha_{s-1,t-1}+\alpha_{s,t-1})\cdot p_t(Z_s \mid X) αs,t=(αs−1,t−1+αs,t−1)⋅pt(Zs∣X)
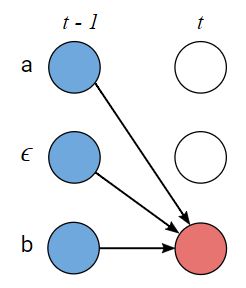
Case 2
上图表示的是语音在两个不同token之间切换的情况。
在这种情况下, α \alpha α的计算公式如下:
α s , t = ( α s − 2 , t − 1 + α s − 1 , t − 1 + α s , t − 1 ) ⋅ p t ( Z s ∣ X ) \alpha_{s,t}=(\alpha_{s-2,t-1}+\alpha_{s-1,t-1}+\alpha_{s,t-1})\cdot p_t(Z_s \mid X) αs,t=(αs−2,t−1+αs−1,t−1+αs,t−1)⋅pt(Zs∣X)
推断计算
我们首先看看CTC的正向推断(Inference)是如何计算的。
在前面的章节我们已经指出,由于对齐有很多种可能的情况,采用穷举法是不现实的。
另一个比较容易想到的方法是:每步只采用最大可能的token。这种启发式算法,实际上就是A*算法。
A*算法计算速度快,但不一定能找到最优解。
一般采用改良的Beam Search算法,在准确率和计算量上取得一个trade off。