深度学习（三十）——Deep Speech, 自动求导

CTC

推断计算（续）

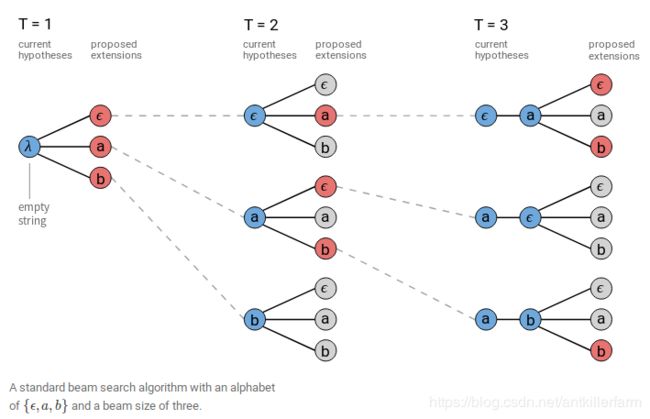
上图是一个Beam Width为3的Beam Search。Beam Search的细节可参见《机器学习（二十三）》。

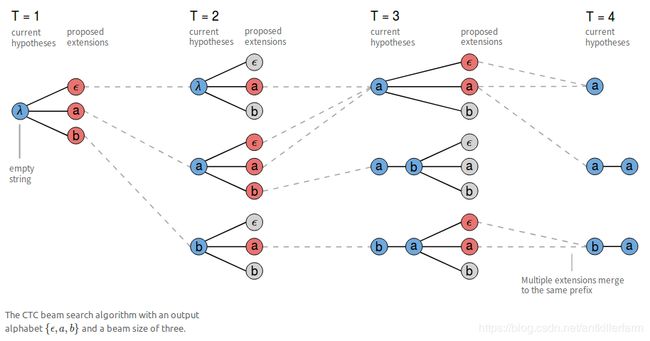
由于语音的特殊性，我们实际上用的是Beam Search的一个变种：

如上图所示，所有在合并规则下，能够合并为同一前缀的分支，在后续计算中，都被认为是同一分支。其概率值为各被合并分支的概率和。

此外，如果在语音识别中，能够结合语言模型的话，将可以极大的改善语音识别的准确率。这种情况下的CTC loss为：

$$Y^{\ast }={\mathrm{argmax}}_{Y}p(Y\mid X)\cdot p(Y{)}^{\alpha }\cdot L(Y{)}^{\beta }$$

其中，$p(Y{)}^{\alpha }$是语言模型概率，而$L(Y{)}^{\beta }$表示词嵌入奖励。

CTC的特性

CTC是条件独立的。

缺点：条件独立的假设太强，与实际情况不符，因此需要语言模型来改善条件依赖性，以取得更好的效果。

优点：可迁移性比较好。比如朋友之间的聊天和正式发言之间的差异较大，但它们的声学模型却是类似的。

CTC是单调对齐的。这在语音识别上是没啥问题的，但在机器翻译的时候，源语言和目标语言之间的语序不一定一致，也就不满足单调对齐的条件。

CTC的输入/输出是many-to-one的，不支持one-to-one或one-to-many。比如，“th”在英文中是一个音节对应两个字母，这就是one-to-many的案例。

最后，Y的数量不能超过X，否则CTC还是没法work。

CTC应用

HMM

如上图所示，CTC是一种特殊的HMM。CTC的状态图是单向的，这也就是上面提到的单调对齐特性，这相当于给普通HMM模型提供了一个先验条件。因此，对于满足该条件的情况，CTC的准确度要超过HMM。

最重要的是，CTC是判别模型，它可以直接和RNN对接。

Encoder-Decoder模型

Encoder-Decoder模型是sequence问题最常用的框架，它的数学形式为：

$$\begin{gathered} H=encode(X) \\ p(Y\mid X)=decode(H) \end{gathered}$$

这里的H是模型的hidden representation。

CTC模型可以使用各种Encoder，只要保证输入比输出多即可。CTC模型常用的Decoder一般是softmax。

参考

https://distill.pub/2017/ctc/

Sequence Modeling With CTC

http://blog.csdn.net/laolu1573/article/details/78791992

Sequence Modeling With CTC中文版

https://mp.weixin.qq.com/s?__biz=MzIzNDQyNjI5Mg==&mid=2247483834&idx=1&sn=3a92eb19858d2cec709af28d2eb69c4a

时序分类算法之Connectionist Temporal Classification

http://blog.csdn.net/u012968002/article/details/78890846

CTC原理

https://www.zhihu.com/question/47642307

语音识别中的CTC方法的基本原理

https://www.zhihu.com/question/55851184

基于CTC等端到端语音识别方法的出现是否标志着统治数年的HMM方法终结？

https://zhuanlan.zhihu.com/p/23308976

CTC——下雨天和RNN更配哦

https://zhuanlan.zhihu.com/p/23293860

CTC实现——compute ctc loss（1）

https://zhuanlan.zhihu.com/p/23309693

CTC实现——compute ctc loss（2）

http://blog.csdn.net/xmdxcsj/article/details/70300591

端到端语音识别（二）ctc。这个blog中还有5篇《CTC学习笔记》的链接。

https://blog.csdn.net/luodongri/article/details/77005948

白话CTC(connectionist temporal classification)算法讲解

Warp-CTC

Warp-CTC是一个可以应用在CPU和GPU上的高效并行的CTC代码库，由百度硅谷实验室开发。

官网：

https://github.com/baidu-research/warp-ctc

非官方caffe版本：

https://github.com/xmfbit/warpctc-caffe

Deep Speech

Deep Speech是吴恩达领导的百度硅谷AI Lab 2014年的作品。

论文：

《Deep Speech: Scaling up end-to-end speech recognition》

代码：

https://github.com/mozilla/DeepSpeech

上图是Deep Speech的网络结构图。网络的前三层和第5层是FC，第4层是双向RNN，Loss是CTC。

主要思路：

1.这里的FC只处理部分音频片段，因此和CNN有异曲同工之妙。

2.论文解释了不用LSTM的原因是：很难并行处理。

参考：

http://blog.csdn.net/xmdxcsj/article/details/54848838

Deep Speech笔记

Deep speech 2

Deep speech 2是Deep speech原班人马2015年的作品。

论文：

《Deep speech 2: End-to-end speech recognition in english and mandarin》

代码：

https://github.com/PaddlePaddle/DeepSpeech

这个官方代码是PaddlePaddle实现的，由于比较小众，所以还有非官方的代码：

https://github.com/ShankHarinath/DeepSpeech2-Keras

不出所料，这里使用CNN代替了FC，音频数据和图像数据一样，都是局部特征很明显的数据，从直觉上，CNN应该要比FC好使。

至于多层RNN或者GRU都是很自然的尝试。论文的很大篇幅都是各种调参，也就是俗称的“深度炼丹”。

论文附录中，如何利用集群进行分布式训练，是本文的干货，这里不再赘述。

EESEN

论文：

《EESEN: End-to-End Speech Recognition using Deep RNN Models and WFST-based Decoding》

苗亚杰，南京邮电大学本科（2008）+清华硕士（2011）+CMU博士（2016）。
个人主页：
http://www.cs.cmu.edu/~ymiao/

官网：

https://github.com/srvk/eesen

eesen是基于Tensorflow开发的，苗博士之前还有个用Theano开发的叫PDNN的库。

自动求导

DL发展到现在，其基本运算单元早就不止CNN、RNN之类的简单模块了。针对新运算层出不穷的现状，各大DL框架基本都实现了自动求导的功能。

论文：

《Automatic Differentiation in Machine Learning: a Survey》

Numerical differentiation

数值微分最大的特点就是很直观，好计算，它直接利用了导数定义：

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

不过这里有一个很大的问题：h怎么选择？选大了，误差会很大；选小了，不小心就陷进了浮点数的精度极限里，造成舍入误差。

第二个问题是对于参数比较多时，对深度学习模型来说，上面的计算是不够高效的，因为每计算一个参数的导数，你都需要重新计算$$f(x+h)$$。

因此，这种方法并不常用，而主要用于做梯度检查（Gradient check），你可以用这种不高效但简单的方法去检查其他方法得到的梯度是否正确。

Symbolic differentiation

符号微分的主要步骤如下：

1.需要预置基本运算单元的求导公式。

2.遍历计算图，得到运算表达式。

3.根据导数的代入法则和四则运算法则，求出复杂运算的求导公式。

这种方法没有误差，是目前的主流，但遍历比较费时间。

Automatic differentiation

除此之外，常用的自动求导技术，还有Automatic differentiation。（请注意这里的AD是一个很狭义的概念。）

类比复数的概念：

$$x=a+bi(i^2=-1)$$

我们定义Dual number：

$$x\mapsto x=x+\dot{x}d(d^2=0)$$

定义Dual number的运算法则：

$$(x+\dot{x}d)+(y+\dot{y}d)=x+y+(\dot{x}+\dot{y})d$$

$$(x+\dot{x}d)(y+\dot{y}d)=xy+\dot{x}yd+x\dot{y}d+\dot{x}\dot{y}{d}^2=xy+(\dot{x}y+x\dot{y})d$$

$$-(x+\dot{x}d)=-x-\dot{x}d$$

$$\frac{1}{x+\dot{x}d}=\frac{1}{x}-\frac{\dot{x}}{x^2}d$$

dual number有很多非常不错的性质。以下面的指数运算多项式为例：

$$f(x)=p_0+p_{1}x+p_2{x}^2+...+p_n{x}^n$$

用$x+\dot{x}d$替换x，则有：

$$\begin{gathered} f(x+\dot{x}d)=p_0+p_1(x+\dot{x}d)+...+p_n(x+\dot{x}d{)}^n \\ =p_0+p_{1}x+p_2{x}^2+...+p_n{x}^n+ \\ {p}_1\dot{x}d+2p_{2}x\dot{x}d+...+n{p}_{n-1}x\dot{x}d \\ =f(x)+f^{\prime }(x)\dot{x}d \end{gathered}$$

可以看出d的系数就是$f^{\prime }(x)$。

参考

https://mp.weixin.qq.com/s/7Z2tDhSle-9MOslYEUpq6g

从概念到实践，我们该如何构建自动微分库

https://mp.weixin.qq.com/s/bigKoR3IX_Jvo-re9UjqUA

机器学习之——自动求导

https://www.jianshu.com/p/4c2032c685dc

自动求导框架综述

https://mp.weixin.qq.com/s/xXwbV46-kTobAMRwfKyk_w

自动求导–Deep Learning框架必备技术二三事