U25%(1,16) and U25%(1,168)on《C4.5:programs for machine learning》
when calculating
U C F U_{CF} UCF(e,N)
CF: Confidence Level(here is 25%)
e:misclassifying counts of current subtree we focus on
N:counts of sub-datasets relevant to current subtree who is under judgment whether to be pruned or not.
“Pr” is short for “Pessimistic error rate”.
U C F U_{CF} UCF(e,N)=Pr= e + 0.5 + C o e f f 2 2 + C o e f f 2 ⋅ { ( e + 0.5 ) [ 1 − e + 0.5 N ] + C o e f f 2 4 } N + C o e f f 2 ① \frac{e+0.5+ \frac{Coeff^2}{2}+ \sqrt{ Coeff^2·\{ (e+0.5)[1- \frac{e+0.5}{N} ]+ \frac{Coeff^2}{4} \} } } {N+Coeff^2}① N+Coeff2e+0.5+2Coeff2+Coeff2⋅{(e+0.5)[1−Ne+0.5]+4Coeff2}①
The method to get C o e f f \ Coeff Coeff is as follows:
C o e f f − D e v i a t i o n [ i − 1 ] D e v i a t i o n [ i ] − D e v i a t i o n [ i − 1 ] = C o n f i d e n c e L e v e l − v a l [ i − 1 ] v a l [ i ] − v a l [ i − 1 ] ② \frac{Coeff-Deviation[i-1]}{Deviation[i]-Deviation[i-1]}=\frac{Confidence \ Level-val[i-1]}{val[i]-val[i-1]}② Deviation[i]−Deviation[i−1]Coeff−Deviation[i−1]=val[i]−val[i−1]Confidence Level−val[i−1]②
Now Let’s analyse the meaning of ② and how to get “i” in formula ②.
What is Deviation and Val?
Val[] = { 0, 0.001, 0.005, 0.01, 0.05, 0.10, 0.20, 0.40, 1.00},
Deviation[] = {4.0, 3.09, 2.58, 2.33, 1.65, 1.28, 0.84, 0.25, 0.00};
for Normal Distribution:
P{X>Deviation[i]}=val[i],
for example:
P{X>2.58}=0.005
--------------------
Now let’s analyse the whole meaning of formula ②
the red line is P ( X > x ) = ∫ x + ∞ 1 2 π e − x 2 2 d x P(X>x)=\int_x^{+∞}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx P(X>x)=∫x+∞2π1e−2x2dx
the blue line is f ( x ) = 1 2 π e − x 2 2 f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} f(x)=2π1e−2x2
and the two points are:
(deviation[i],val[i])=(0.25,0.4)
(deviation[i-1,val[i-1])=(0.84,0.2)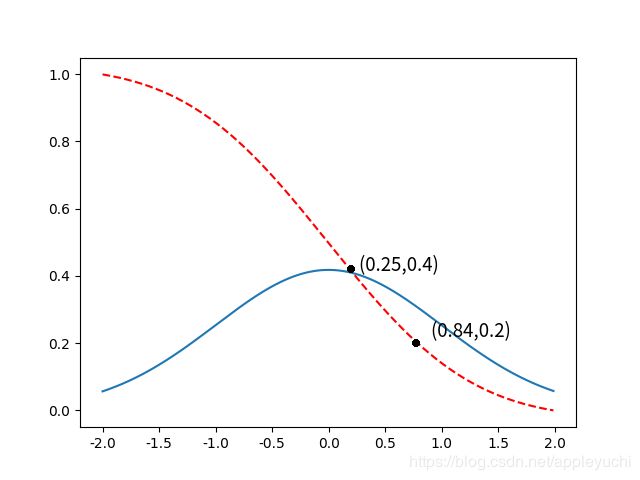
Let’s amplify the above figure to the following picture:
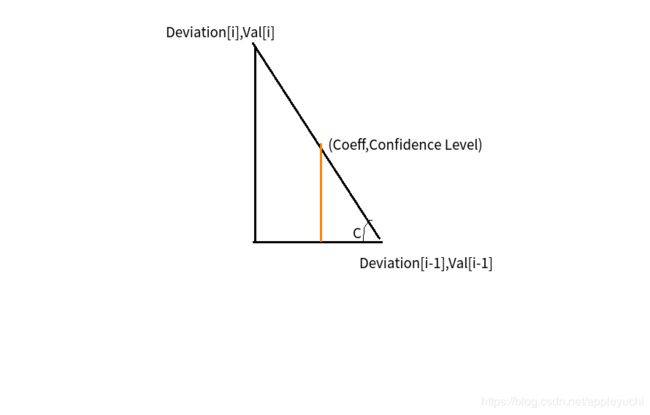
so tan C= V a l [ i ] − V a l [ i − 1 ] D e v i a t i o n [ i − 1 ] − D e v i a t i o n [ i ] = C o n f i d e n c e L e v e l − V a l [ i − 1 ] D e v i a t i o n [ i − 1 ] − C o e f f \frac{Val[i]-Val[i-1]}{Deviation[i-1]-Deviation[i]}=\frac{Confidence\ Level-Val[i-1]}{Deviation[i-1]-Coeff} Deviation[i−1]−Deviation[i]Val[i]−Val[i−1]=Deviation[i−1]−CoeffConfidence Level−Val[i−1]
then we can get ②and compute C o e f f Coeff Coeff and C o e f f 2 Coeff^2 Coeff2
but how to get “i” in above formula?
when V a l [ i − 1 ] < C o n f i d e n c e l e v e l ≤ V a l [ i ] Val[i-1]<Confidence \ level≤Val[i] Val[i−1]<Confidence level≤Val[i]
is satisfied,
we get “i”.
when Confidence Level=0.25
i=7
val[i-1]=0.2
val[i]=0.4
deviation[i-1]=0.84
deviation[i]=0.25
substitute the above values in ②
we get Coeff=0.6925
then,
C o e f f 2 = 0.479556 Coeff^2=0.479556 Coeff2=0.479556
--------------------
**Now Let’s calculate **
U 0.25 ( 1 , 16 ) U_{0.25}(1,16) U0.25(1,16)
CF=0.25
e=1
N=16
C o e f f 2 = 0.479556 Coeff^2=0.479556 Coeff2=0.479556
We’ll get :
Pr=
1 + 0.5 + 0.479556 2 + 0.479556 ⋅ { ( 1 + 0.5 ) [ 1 − 1 + 0.5 16 ] + 0.479556 4 } 16 + 0.479556 \frac{1+0.5+ \frac{0.479556}{2}+ \sqrt{ 0.479556·\{ (1+0.5)[1- \frac{1+0.5}{16} ]+ \frac{0.479556}{4} \} } } {16+0.479556} 16+0.4795561+0.5+20.479556+0.479556⋅{(1+0.5)[1−161+0.5]+40.479556}=0.156681
N·Pr=16×0.156681=2.507
Compared with Quinlan’s book page 42th:
Now Let’s calculate
U 0.25 ( 1 , 168 ) U_{0.25}(1,168) U0.25(1,168)
CF=0.25
e=1
N=168
Pr= 1 + 0.5 + 0.479556 2 + 0.479556 ⋅ { ( 1 + 0.5 ) [ 1 − 1 + 0.5 168 ] + 0.479556 4 } 168 + 0.479556 = 0.015536 \frac{1+0.5+ \frac{0.479556}{2}+ \sqrt{ 0.479556·\{ (1+0.5)[1- \frac{1+0.5}{168} ]+ \frac{0.479556}{4} \} } } {168+0.479556}=0.015536 168+0.4795561+0.5+20.479556+0.479556⋅{(1+0.5)[1−1681+0.5]+40.479556}=0.015536
N ⋅ U 0.25 ( 1 , 168 ) = N ⋅ P r = 168 ⋅ 0.015536 = 2.61 N·U_{0.25}(1,168)=N·Pr=168·0.015536=2.61 N⋅U0.25(1,168)=N⋅Pr=168⋅0.015536=2.61
Compared with Quinlan’s Book on Page 42th:

The code to veriy the above value:
/*************************************************************************/
/* */
/* Statistical routines for C4.5 */
/* ----------------------------- */
/* */
/*************************************************************************/
#include
#include
/*************************************************************************/
/* */
/* Compute the additional errors if the error rate increases to the */
/* upper limit of the confidence level. The coefficient is the */
/* square of the number of standard deviations corresponding to the */
/* selected confidence level. (Taken from Documenta Geigy Scientific */
/* Tables (Sixth Edition), p185 (with modifications).) */
/* */
/*************************************************************************/
float CF=0.25;
float Val[] = { 0, 0.001, 0.005, 0.01, 0.05, 0.10, 0.20, 0.40, 1.00},//概率
Dev[] = {4.0, 3.09, 2.58, 2.33, 1.65, 1.28, 0.84, 0.25, 0.00};//这个就是分位点
// P{X>Dev[i]}=val[i],
// according to standardized normal distribution N(0,1)
// for example:
// P{X>2.58}=0.005,
float AddErrs(float N, float e)//叶子的悲观错误
{
static float Coeff=0;
float Val0, Pr;
if ( ! Coeff )//compute only once when pruning trees
{
/* Compute and retain the coefficient value, interpolating from
the values in Val and Dev */
int i;
i = 0;
while ( CF > Val[i] ) i++;//这里可以看到,是根据置信度对悲观错误数量进行计算的。
//但是呢,也没有像理论中直接计算“悲观错误率”
Coeff = Dev[i-1] +
(Dev[i] - Dev[i-1]) * (CF - Val[i-1]) /(Val[i] - Val[i-1]);
Coeff = Coeff * Coeff;
printf("Coeff=%f\n",Coeff);//CF定下来以后,Coeff就是定的
}
if ( e < 1E-6 )
{
return N * (1 - exp(log(CF) / N));
}
else
if ( e < 0.9999 )
{
Val0 = N * (1 - exp(log(CF) / N));
return Val0 + e * (AddErrs(N, 1.0) - Val0);//这里在进行递归调用
}
else
if ( e + 0.5 >= N )
{
return 0.67 * (N - e);
}
else
{
float fenzi;
fenzi=(
e + 0.5 + Coeff/2+ sqrt
(
Coeff *
(
(e + 0.5) * (1 - (e + 0.5)/N) + Coeff/4
)
)
);
printf("fenzi=%f\n",fenzi);
Pr = (
e + 0.5 + Coeff/2+ sqrt
(
Coeff *
(
(e + 0.5) * (1 - (e + 0.5)/N) + Coeff/4
)
)
)
/ (N + Coeff);
printf("Pr=%f\n",Pr);
return (N * Pr - e);
}
}
int main()
{
float result=AddErrs(16, 1);
printf("result=%f\n",result);
exit(0);
}
running method:
gcc -o stats stats.c -lm
./stats
the result is:
Coeff=0.479556
fenzi=2.582031
Pr=0.156681
result=1.506894
