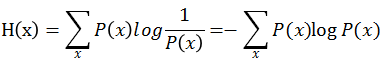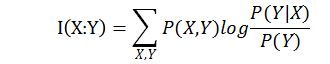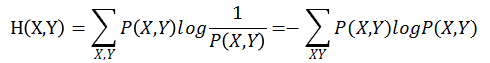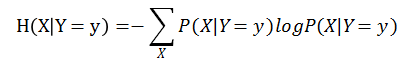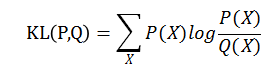自然语言处理学习（一）之概述小结

一．概述

1. 现状

现代nlp的主要任务已经跨越对词的研究，发展到了对句子研究，即句法、句义及句子生成的研究，已经能较好的解决句子层面的问题，但是尚未达到完全解决篇章层面的问题，尚不足以达到较为自由的人机交互。

专业技术：完全句法分析、浅层句法分析、信息抽取、词义消歧、潜在语义分析、文本蕴含和指代消解。

1. 问题：

1. 语法解析：大规模的中文分析、词性标注系统已基本达到商用，但是句法解析方面还存在精度问题。
2. 语义解析: 命名实体识别、语义块已经获得了较高的精度。人工智能对知识库的研究历史悠久，已经形成了一整套的知识库的架构和推理体系。实现句子到知识库的主要方法是语义角色标注系统，但在整句理解，精度依赖于句法解析系统。

二、三个平面的语义研究

1.词汇和本体论（关于语义意义）

词汇的语义--------->对事物的编码

人在组织概念的认知机制----->范畴化

本体论----------->对领域内的真实存在做出客观描述，而不依赖于特定语言

2.格语法及框架（语法能否脱离语义而独立存在）

语义和语法相互依存，只能在抽象意义上分开，而在具体语言实例看做一体。

“格”：句子中体词（名词、代词等）和谓词（动词、形容词等）之间的及物关系。一旦被确定，句子的语义结构就被确定。

三部分：基本规则、词汇部分和转换部分

局限性：只研究了名词和动词的关系，没有考虑其他的语义关系

3. 语义角色研究

在格的影响下产生。适用于更复杂、多样的

三、词汇和分词技术

1.分词规范

  1）《北大（中科院）词性标注》、《现代汉语语料库加工规范》《北大现代汉语语料库基本加工规范》

  北大标准包含40类词，兼顾了词的语法特征和语义特征，但是语义特征并不完备。

  2）《宾州树库中文分词规范》

2.分词标准

 1）粗粒度：词语作为最小标准。用于自然语言处理各种应用

 2）细粒度：语素作为最小标准。用于搜索引擎

 常用：索引时使用细粒度保证召回，查询使用粗粒度保证精度

3. 歧义

交集型歧义切分、组合型歧义切分------->词典+语言模型

1. 词汇的构成

三个特性：稳固性、常用性和能产性（主要表现在产生新的词汇）

未登录词：九成专有名词、一成的通用新词和专业术语。未登录词识别即对专有名词的识别。

命名实体：专有名词和数字、日期等词

算法：基于半监督的条件随机场算法，处理不同领域的专名识别具有较低的成本和较好的效果。

ICTCLAS（NLPLR）中文自然语言处理从词法分析时代跨入了句法分析时代

四、概率图模型

 1.概率论概念

     4.1概率

      联合概率分布、边缘概率分布、条件概率分布、独立性和条件独立性

     4.2 信息熵

      概率是对事件确定性的度量，信息（信息量和信息熵）是对事物不确定性的度量。

      信息量：离散信源信号发生的不确定性，在NLP中代表特征的不确定性。

                    I(x)=-logP(x)

      信息熵：离散信源信号发生的平均不确定性，在NLP中代表特征的不确定性的均值。

      

              1)信息熵的本质是对信息量的期望

              2)信息熵上是对随机变量不确定性的分布

              3)平均分布是最不确定的分布

     4.3 互信息和平均互信息

      定义：x的后验概率与先验概率比值的对数称为y对x的互信息量，也称互信息。在NLP中是特征对应标签的不确定性，衡量了对称性。

      

     性质：(1)互信息可以认为是接受到信息X,对信源Y的不确定性的消除。

            (2)互信息是对称的。

      平均互信息(信息增益)：

      

      4.4 联合熵

      定义：借助联合概率分布对熵的自然推广，在NLP中是训练集总体不确定性。

      公式：

      

     4.5 条件熵

      定义：利用条件概率分布对熵的推广，熵度量的是随机变量X的不确定性，条件熵度量的则是已知Y=y后，X的不确定性。在NLP中给定标签的情况下，特征的不确定性，衡量了差异性。

      公式：

      

       链式规则：

      H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)

      I(X;Y)+H(X,Y)=H(X)+H(Y)

       4.6交叉熵

      定义：衡量两个概率分布的差异性，在NLP中是学习阶段中，不同时间点间的误差（损失函数）。在Logistic中交叉熵为其损失函数。

      公式：

       

        4.7相对熵

        定义：定义于随机变量X的状态空间熵的两个概率分布P(x)和Q(x)，可以用相对熵衡量其差异，在NLP中同样是不同时点间的误差，非对称性

 公式：

        

         KL(P,Q)又称为P(x)和Q(x)的KL散度，并且KL(P,Q)不等于KL(Q,P)

五概率图模型

   5.1定义：结合了概率论和图论，用图模式表达基于概率相关关系的模型的总称，目的是通过引入图模型可以将复杂的问题进行适当的分解，使得问题结构化。

   5.2 三个基本问题

      5.2.1模型的表示

      从图模型表示上来说，可以分为贝叶斯网络和马尔科夫随机场，

贝叶斯网络采用有向无环图来表达事件的因果关系。每一个节点对应于一个先验概率分布或条件概率分布，于是联合概率分布就可以分解成单节点对应分布的乘积。

马尔科夫随机场采用无向图来表达变量间的相互作用。变量之间没有明确因果关系，因此联合概率会表达为一系列势函数乘积，通常乘积积分并不为1，因此需要通过归一化形成有效的概率分布。

      5.2.2模型的学习

      将给定的图模型，形式化为数学公式。

      精度影响因素：1.训练集对总体的代表性

                    2.模型算法理论基础及所针对的问题，不同模型在不同问题上有更好的表现。

                    3.模型复杂度，参数估计精度越高，一般复杂度就越高，学习效率就越低。

      5.2.3模型的预测

      将新输入的样本通过学习后的模型，选取后验概率指向的最有可能的标签作结果，即

根据样本判定每种观测序列Y的概率。

   5.3 产生式模型和判别式模型

     5.3.1产生式模型

     定义：在有限样本条件下，寻找不同数据间的最优分类面，目标是实现分类

     核心：估计条件概率分布

代表模型：最大熵模型、条件随机场模型

         条件随机场模型可以看做最大熵模型的序列化模型扩展。

优点：1.面向分类边界的训练

      2.清晰分辨出类别之间的差异特征

      3.可用于多分类的学习

      4.比判别式模型简单

缺点：1.不能反应数据本身的特性，只能用于识别

      2.数据量很大时，效果不高

      3.缺乏灵活的建模工具和插入先验知识的方法

    评价：所有的序列标注和结构化学习  

     5.3.2判别式模型

     定义：建立样本的联合概率分布，再利用模型推理预测，要求样本尽可能大。

     核心：估计联合概率分布

     代表模型：朴素贝叶斯模型、隐马尔科夫模型

            隐马尔科夫模型可以看做朴素贝叶斯模型的序列化模型拓展。

     优点：1.面向整体数据的分布

           2.可以反映同类数据本身的相似度

           3.模型可以进行增量学习

           4.可用于数据不完整情况

     缺点：1.计算所有变量的联合概率，占用资源大

           2.类别识别精度有限

           3.学习和计算过程复杂

     评价：性能较低，适用于词性标注等