计算机视觉中的多视图几何——第一章:2D摄影几何(1.点和直线的齐次表示)
计算机视觉中的多视图几何——第一章:2D摄影几何(1.点和直线的齐次表示)
- 1.1平面几何
- 1.2 2D摄影平面
- 1.2.1 点和直线
- 1.2.2 理想点与无穷远线
- 1.2.3 二次曲线与对偶二次曲线
- 参考文献:
引言: 由于在三维重构方面的工作中,涉及到大量的坐标系转化、图像矫正等相关知识,因此个人决定有必要系统的学习一下多视几何知识。于是开始啃被视为“”视觉圣经‘’《计算机中的多视图几何》。为了便于自己更准确深刻的理解相关知识,遂写成博客形式的读书笔记。为避免自己理解偏差而误导他人,因此博客内容主要以书本内容为主,偶尔加入自己的注释,欢迎相关人士交流和建议。
1.1平面几何
自笛卡尔之后,人们开始利用代数的观点推导几何理论
一个点等同于某个坐标系下的是一个矢量;
一条直线也等同于一个矢量;
一段圆锥截线(二次曲线)用一个对称矩阵表示;
矢量即为点,对称矩阵即为二次曲线
1.2 2D摄影平面
行和列矢量:矢量空间之间的线性映射可以用矩阵来表示。通常情况下一个矩阵与一个矢量的积还是矢量,矩阵可以被行矢左乘,被列矢右乘,所得矢量即为该映射下的象;
x总表示列矢量。转置 x T x^T xT为行向量;
因此,点表示为列矢量 ( x , y ) T (x,y)^T (x,y)T,方程记做:x= ( x , y ) T (x,y)^T (x,y)T,两边都是列矢量;
1.2.1 点和直线
直线的齐次表示:
直线方程:ax+by+c=0;
矢量表示: ( a , b , c ) T (a,b,c)^T (a,b,c)T;系数a、b、c的值不同,代表不同的直线;
推导:对于k ≠ \neq ̸= 0时, ( a , b , c ) T (a,b,c)^T (a,b,c)T和k* ( a , b , c ) T (a,b,c)^T (a,b,c)T是同一条直线,两个相差一个非零缩放因子的矢量是等价的,这种等价关系下的矢量等价类被称作是齐次矢量 , 任何具体的 ( a , b , c ) T (a,b,c)^T (a,b,c)T都是等价类的一个代表。
在 I R 3 − ( 0 , 0 , 0 ) T IR^3-(0,0,0)^T IR3−(0,0,0)T中的矢量等价类的集合组成射影空间 I P 2 IP^2 IP2;
直线在射影空间的齐次表示:矢量等价类—— ( a , b , c ) T (a,b,c)^T (a,b,c)T是射影空间 I P 2 IP^2 IP2的元素
点的齐次表示:
点矢量:x= ( x , y ) T (x,y)^T (x,y)T;
直线:I= ( a , b , c ) T (a,b,c)^T (a,b,c)T;
点在直线上:ax+by+c=0,即(x,y,1)I=0;其中x表示为三维矢量.
推导:对任意非零k和直线I,方程 ( k x , k y , k ) T (kx,ky,k)^T (kx,ky,k)TI=0的充要条件为 ( x , y , 1 ) T (x,y,1)^T (x,y,1)TI=0;因此, k ≠ k\neq k̸= 0的不同值构成的矢量集 ( x , y , 1 ) T (x,y,1)^T (x,y,1)T看作是 I R 2 IR^2 IR2内点 ( x , y ) T (x,y)^T (x,y)T的一种表示,因此点也可以用齐次矢量表示;
一个点的任何一个齐次矢量的表示形式为x= ( x 1 , x 2 , x 3 ) T (x_1,x_2,x_3)^T (x1,x2,x3)T,并表示 I R 2 IR^2 IR2的点x= ( x 1 / x 3 , x 2 / x 3 ) T (x_1/x_3,x_2/x_3)^T (x1/x3,x2/x3)T,于是点作为齐次矢量同样也是 I P 2 IP^2 IP2的元素;
点的齐次表示: 齐次矢量(x1,x2,x3)T是射影空间IP2的元素;点的齐次坐标是三维的 ( x 1 , x 2 , x 3 ) T (x_1,x_2,x_3)^T (x1,x2,x3)T,非齐次坐标是二维的(x,y) T ^T T;
结论 1.1 点x在直线I上的充要条件x T ^T TI=0
自由度: 确定一个点需要x,y两个坐标; 确定一条直线需要两个未知数(齐次表示中的a: b :c的比率,非齐次表示的斜率和截距);
直线的交点: 两直线I和I’ 的交点x=I × \times × I’
两点的连线: 过两点x和x’的连线I=x × \times ×x’
1.2.2 理想点与无穷远线
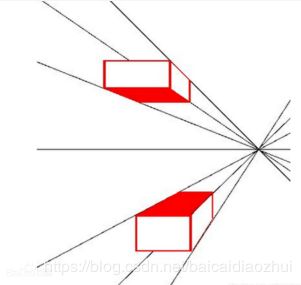
在仿射平面上,引入了理想元素——直线上的无穷点,一组平行线有共同的无穷远点,不同的平行线组有不同的无穷远点,平面上各方向的无穷远点构成该平面上的无穷远线[1];
- 平行线的交点
- 平行线:ax+by+c=0和ax+by+c’=0,别用齐次矢量表示为 I = ( a , b , c ) T I=(a,b,c)^T I=(a,b,c)T和 I = ( a , b , c ′ ) T I=(a,b,c')^T I=(a,b,c′)T;
- 交点:x = I × \times × I’ = (c’-c)(b,-a,0) T ^T T,忽略标量因子(c’-c)得点坐标(b,-a,0) T ^T T;
- 非齐次坐标: ( b / 0 , − a / 0 ) T (b/0,-a/0)^T (b/0,−a/0)T,可解释为该坐标点无限大,可知平行线相较于无限远点;
- 齐次坐标为 ( x , y , 0 ) T (x,y,0)^T (x,y,0)T 的点不与 I R 2 IR^2 IR2 上的任何有限点对应。
- 理想点
- 在射影空间IR 2 ^2 2中,齐次矢量x= ( x 1 , x 2 , x 3 ) T (x_1,x_2,x_3)^T (x1,x2,x3)T,则:
- 有限点:当 x 3 ≠ 0 x_3\neq0 x3̸=0时,x对应为有限点;
- 理想点:当 x = 0 x=0 x=0时,x对应无穷远点,称为理想点;
所有理想点的集合可以写成 ( x 1 , x 2 , 0 ) T (x_1,x_2,0)^T (x1,x2,0)T,并由比率 x 1 : x 2 x_1:x_2 x1:x2确定, 可理解为平行线的斜率相同,且相交于同一个理想点,因此斜率确定则理想点确定
- 无穷远线:
在射影平面 I P 2 IP^2 IP2中,任意两条相异的直线都相交于一点,任意两个相异的点都在一条直线上;而在欧式几何 I R 2 IR^2 IR2中却不成立;
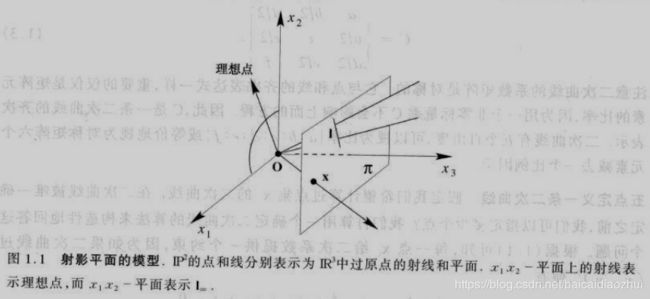
- 射影平面的模型
把 I P 2 IP^2 IP2看作是 I R 3 IR^3 IR3中一种射线的集合;该集合的所有矢量 k ( x 1 , x 2 , x 3 ) T k(x_1,x_2,x_3)^T k(x1,x2,x3)T 。当k变化时形成过原点的射线, I R 3 IR^3 IR3中一条射线为 I P 2 IP^2 IP2中的一个点,而 I R 3 IR^3 IR3中过原点的平面则为 I P 2 IP^2 IP2中的直线。
- 对偶原理: 2D射影几何中的任何定理都有一个对应的对偶定理,他可以通过互换原定理中的点和线的作用而导出
+过两点的直线与过直线的两点对偶;
1.2.3 二次曲线与对偶二次曲线
欧式几何中常见的二次曲线有:双曲线、椭圆、抛物线,二次曲线由平面上的二次方程描述。经典理论中,这三类曲线是由不同方向的平面与圆锥相交所产生的截线。
非齐次坐标中的二次方程为:
a x 2 + b x y + c y 2 + d x + e y + f = 0 ax^2+bxy+cy^2+dx+ey+f=0 ax2+bxy+cy2+dx+ey+f=0
对变量进行替换, x → x 1 / x 3 , y → x 2 / x 2 , x\rightarrow x_1/x_3,y\rightarrow x_2/x_2, x→x1/x3,y→x2/x2, 进行“齐次化”得到:
a x 1 2 + b x 1 x 2 + c x 2 2 + d x 1 x 3 + e x 2 x 3 + f x 3 2 = 0 ax_1^2+bx_1x_2+cx_2^2+dx_1x_3+ex_2x_3+fx_3^2=0 ax12+bx1x2+cx22+dx1x3+ex2x3+fx32=0
矩阵形式表示为:
x T C x x^TCx xTCx
其中二次曲线系数矩阵C为:
[ a b / 2 d / 2 b / 2 c e / 2 d / 2 e / 2 f ] \begin{bmatrix} a & b/2 & d/2 \\ b/2 & c & e/2 \\ d/2 & e/2 & f \end{bmatrix} ⎣⎡ab/2d/2b/2ce/2d/2e/2f⎦⎤
其中二次曲线的系数矩阵 C C C是对称矩阵,且非零标量乘以 C C C不会影响以上方程,因此 C C C是一条二次曲线的其次表示,二次曲线有五个自由度,可以视作比率{ a : b : c : d : e : f a:b:c:d:e:f a:b:c:d:e:f}或视为对称矩阵六个元素减去一个比例因子。
- 五个点可以提供五个约束条件,即可定义一条二次曲线
当二次曲线过点 ( x i , y i ) T (x_i,y_i)^T (xi,yi)T有二次曲线方程可写为:
a x i 2 + b x i y i + c y i 2 + d x i + e y i + f = 0 ax_i^2+bx_iy_i+cy_i^2+dx_i+ey_i+f=0 axi2+bxiyi+cyi2+dxi+eyi+f=0
将二次曲线的系数矩阵 C C C写成一个六维向量c= ( a , b , c , d , e , f ) T (a,b,c,d,e,f)^T (a,b,c,d,e,f)T;当已知五个二次曲线上的点时,得到方程组的矩阵形式如下:
[ x 1 2 x 1 y 1 y 1 2 x 1 y 1 1 x 2 2 x 2 y 1 y 2 2 x 2 y 2 1 x 3 2 x 3 y 3 y 3 2 x 3 y 3 1 x 4 2 x 4 y 4 y 4 2 x 4 y 4 1 x 5 2 x 5 y 5 y 5 2 x 5 y 5 1 ] c = 0 \begin{bmatrix} x_1^2 & x_1y_1 &y_1^2&x_1 &y_1&1 \\ x_2^2 & x_2y_1 &y_2^2&x_2 &y_2&1 \\ x_3^2 & x_3y_3 &y_3^2&x_3 &y_3&1 \\ x_4^2 & x_4y_4 &y_4^2&x_4 &y_4&1 \\ x_5^2 & x_5y_5 &y_5^2&x_5 &y_5&1 \end{bmatrix}c=0 ⎣⎢⎢⎢⎢⎡x12x22x32x42x52x1y1x2y1x3y3x4y4x5y5y12y22y32y42y52x1x2x3x4x5y1y2y3y4y511111⎦⎥⎥⎥⎥⎤c=0
- 二次曲线的切线
过(非退化)二次曲线 C C C上的点的切线由 I = C C C x 确定
- 对偶二次曲线
- 以上定义的二次曲线 C C C由于是点的方程,因此更准确的说应为点二次曲线;根据射影空间的对偶原理可以得到一个由直线的方程定义的二次曲线,也称为对偶二次曲线;
- 对偶二次曲线的系数矩阵大小也为 3 × 3 3\times3 3×3,记做 C ∗ C^* C∗;取二次曲线的切线为I,则有
I T C ∗ I = 0 I^ T C^* I=0 ITC∗I=0
当 C C C为非奇异矩阵时, C ∗ = C − 1 C^*=C^{-1} C∗=C−1,所以有:
I T C − 1 I = 0 I^ T C^{-1} I=0 ITC−1I=0
+对偶二次曲线有五个自由度,一般位置上的五条线可定义一条对偶二次曲线;
- 退化二次曲线
非满秩矩阵 C C C所定义的二次曲线称作退化二次曲线,退化的点二次曲线包含两条线(秩2)或一条重线(秩1)
参考文献:
1、计算机视觉中的多视图几何。