SSR
摘要:我们证明了利用分割步骤提高基于稀疏的图像重建算法性能的有效性。具体来说,我们将关注视网膜光学相干断层扫描(OCT)重构,提出一种新的基于分割的稀疏表示重构框架,称为基于分割的稀疏重构segmentation based sparse reconstruction(SSR)。SSR方法利用自动分割的视网膜层信息,构造层次特定的结构字典。此外,SSR方法有效地利用了每个分割层内的patch相似性,提高了重建性能。我们在临床级视网膜OCT图像上的实验结果证明了该方法对OCT图像去噪和插值的有效性。
1简介
光学相干层析成像(OCT)是一种非侵入性成像技术,广泛应用于各种医学领域,尤其是眼科诊断领域。眼科OCT图像的自动远程分析在眼病[3]的诊断和研究中越来越普遍。然而,基于采样的散斑和检测器噪声会破坏OCT图像。另一方面,为了加快采集过程,临床OCT图像[3]-[6]的采集往往采用相对较低的空间采样率。高噪声和低空间采样率都对OCT图像的自动分析性能乃至手动分析性能产生负面影响,需要分别采用有效的去噪和插值技术. 去噪和插值是图像处理[7]中两个著名的重建问题。在过去的十年里,各种各样的模型被提出来重建高质量的OCT图像为各种应用[8]-[17]。经典的重建方法通常是建立一个基于平滑先验的模型(如各向异性滤波、Tikhonov滤波和总变异[9]),并在空间域内重建图像。最近的一些方法改变了将退化图像输入到另一个域中(例如,使用小波变换[18]、对偶树复小波变换[19]和曲率变换[20])。虽然基于变换的方法(如小波)通常比空间域方法具有更好的重建性能,但它们是建立在一个固定的数学模型上的,对于表示结构的眼内OCT体积可能具有有限的适应性。 受人类视觉系统[22]稀疏编码机制的启发,稀疏表示被证明是许多图像处理应用[4]、[23]-[30]的强大工具。稀疏表示将输入图像分解为一个过完备的基函数字典的线性组合。可以选择基函数从一组训练图像中提取类似于[31]的输入图像,从而可以更自适应地表示特定的特征。最近的一些工作也将稀疏表示应用于OCT图像重建问题[4]、[6]、[12]、[14]-[16]、[24]、[32]-[34]。虽然不同的视网膜层具有不同的病理结构[35]-[37]甚至斑纹模式,但大多数稀疏重建方法只训练一个通用字典来表示人眼OCT图像中的复杂结构和纹理。 上述传统的稀疏模型直接分解每个局部图像块。测试块中的高噪声和字典原子[23]中的高相关性都会误导稀疏分解过程,从而对最终的重构产生负面影响。最近,一种非局部稀疏重建模型[38]-[40]被引入,该模型利用非局部斑块的自相似性来改进重建。具体来说,对于每一个处理过的patch,基于非局部的稀疏模型都会从整个图像(或者一个大的搜索窗口)中搜索相似的patch,然后在字典[40]上对相似的patch进行联合分解,得到一个更加精确的稀疏解。然而,非局部稀疏表示需要搜索整个图像才能找到相似的patch,这就造成了很高的计算量,同时也会受到OCT图像中较大噪声的干扰。因此,如何构造有效的冗余字典来表示复杂结构,有效地利用patch自相似性进行精确的稀疏分解是稀疏重建模型的两个关键问题。 本文利用分割算法对OCT图像进行重构。我们特别关注视网膜,这是一种分层结构,每一层都有自己的特定特征。注意,由于每一层的结构单元大小、形状和分布不同,导致产生散斑,因此,预计每一层的信噪比模型为不同的[3]、[35]、[36]、[41]。此外,病理结构具有明显的特点,出现在特定的层。例如,drusenoid结构出现在视网膜色素上皮(RPE)层[42]的正下方或正上方,而与老年性黄斑变性相关的高反射病灶预计不会出现在神经纤维层(NFL)[43]。 利用层间结构信息,我们提出了一种基于分割的稀疏重建(SSR)模型,提出了一种快速、准确的重建算法。我们的一般方法是首先利用一个基于图的算法[35]自动分割视网膜OCT图像的多层。然后,对于每一层,SSR都构造一个专用的结构字典以使其更好表示该层的解剖和病理结构。最后,SSR 没有搜索整幅图像,而是有效地搜索每一层中相似的patch,利用每一层中patch的相似性来改进稀疏分解。 注意,基于分段的去噪策略已经被应用于其他几个图像去噪问题[44]-[46]。与此相反,本文提出了一种基于分割的视网膜OCT图像稀疏表示(SSR)模型,该模型利用分割后的层信息提高了稀疏重建模型的有效性和效率。具体来说,我们论文的主要贡献如下1. SSR方法引入了一种基于层分割的方法
结构字典的构建策略,有效地保存了OCT图像中的解剖和病理结构。
2. SSR方法提出了一种基于层分割的方法
稀疏重建策略,利用分层信息显著加快相似patch的搜索过程,利用相似patch之间的相关性提高重建性能。
本文的其余部分组织如下。第二部分简要回顾了稀疏重建模型和非局部均值重建模型。第三节介绍了一种用于OCT图像去噪和插值的SSR方法。第四部分为临床OCT数据的实验结果。第五部分为本文的结论,并对今后的工作提出建议。
2背景:稀疏重建模型和基于非局部均值的重建模型
A 稀疏重建模型给定一个退化图像,最稀疏重建模型首先将输入图像划分为ϒ重叠补丁Xi∈Rn×m i = 1, 2,…,ϒ。每个patch Xi的向量形式记为Xi∈Rq×1(q = n×m),通过字典排序得到。对于去噪问题,稀疏重建模型假设干净的视网膜OCT信号可以很好地由字典中选取的几个原子的加权线性组合表示(D∈Rq×z,q < z),而噪声不能在字典上分解。因此,去噪问题的稀疏重构模型可以表示为:
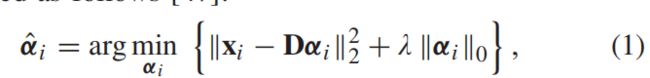
αi∈Rz×1代表xi的稀疏系数向量,||αi||0是 l0-norm,计数αi非零系数的数量。为了解决(1),主要考虑两个方面:
1)字典D结构,2)稀疏系数向量αi估计。为了解决第一个问题,流行算法[31]、[48]从多个相关的采样patch H = {x1,…,xz}中训练出一个字典,其中Z为训练patch的数量。具体来说,字典D可以通过以下优化问题进行训练:
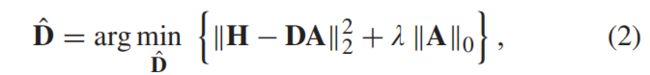
其中A= {αi,…, αZ }为h的稀疏系数矩阵,该方程可以用K-SVD算法[31]求解。解决第二个问题,这是一个NP-hard[49],正交匹配追踪(OMP)[50]算法可以利用获得的近似解稀疏系数向量αˆi。然后,我们可以使用Dαˆi重建相关的补丁(patch)和重建的补丁都回到原来的位置来创建最终的去噪图像。
对于图像插值问题,我们首先将原始的高分辨率图像表示为YH∈RN×M,抽取算子表示为S,相应的低分辨率图像表示为YL = SYH∈R(N/S)×(M/S)。考虑到观测YL退化图像,图像插值的目的是获取YˆH, YˆH≈YH。为解决插值问题,最近的稀疏重建模型[51]试图推断高分辨率空间χH和低分辨率空间χL之间稀疏系数和字典的关系。在[51],杨等人联合训练低分辨率字典DL和高分辨率字典DH,确保空间χL中的稀疏系数αLi与空间χH中的稀疏系数αHi相同。 灵感来自杨等人的工作。 另外,我们利用半耦合学习算法构造匹配的字典DL和DH,然后训练映射函数M来链接稀疏系数αLi和αHi[4]。 在获得空间χL和χH之间的关系之后,稀疏重建模型可以首先找到每个观察片xLi的稀疏系数αLi,然后通过利用高来恢复潜像片xHi以及相应的高分辨率图像Y H. 解析字典DH和映射函数M.
B.非局部均值重建模型
对于图像去噪和插值问题,另一个非常有效的重建模型是非局部手段,它利用了图像固有的自相似性[52]。 具体地,对于从劣化图像提取的每个块xi,非局部均值方法首先从整个图像(或大搜索窗口)中搜索与xi具有最高相似度的W块。 可以通过两个补丁之间的强度差异的平方2范数来测量相似性:
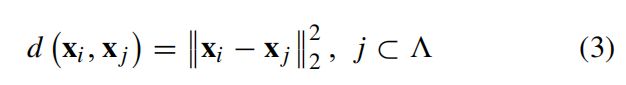
其中Λ是一个包含整个图像中所有补丁的索引的集合。 然后,通过加权平均滤波或补丁相似性惩罚来处理发现相似的补丁,以分别实现去噪[52]或插值[53]。