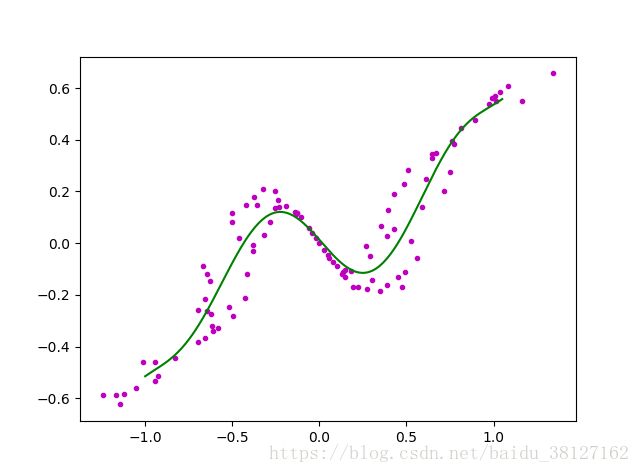
最小二乘法多项式曲线拟合原理与实现（数学公式详细推导，代码方面详细注释）

1. 最小二乘法概念：
   最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法

2. 推导过程

   给定函数y=f(x)，在点 x1 x 1 , x2 x 2 , x3 x 3 ,,,, xn x n 处的函数值 y1 y 1 ， y2 y 2 ， y3 y 3 ，，，， yn y n
   求以多项式p(x)= a0 a 0 + a1 a 1 x+ a2 a 2 x2 x 2 +……+ an a n * xk x k 使得
   
   为了求得负荷条件的a值，对等式右边对 ai a i i=0,1,2….k 求偏导，得到结果为k+1个等式：
   
   
   …..
   

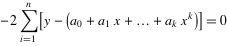
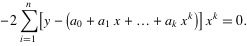
将方程整理，得到：

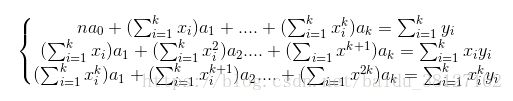
把这些等式表示成矩阵的形式，就可以得到下面的矩阵:

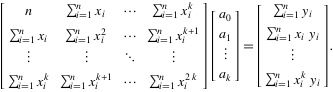
3 代码实现：
利用python语言来进行实现曲线拟合

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
import random

fig = plt.figure()
ax = fig.add_subplot(111)

#阶数为9阶
order=9

#生成曲线上的各个点
x = np.arange(-1,1,0.02)
y = [((a*a-1)*(a*a-1)*(a*a-1)+0.5)*np.sin(a*2) for a in x]

# 生成的曲线上的各个点偏移一下，并放入到xa,ya中去
i = 0
xa = []
ya = []
for xx in x:
    yy = y[i]
    d = float(random.randint(60, 140)) / 100
    # ax.plot([xx*d],[yy*d],color='m',linestyle='',marker='.')
    i += 1
    xa.append(xx * d)
    ya.append(yy * d)

'''''for i in range(0,5): 
    xx=float(random.randint(-100,100))/100 
    yy=float(random.randint(-60,60))/100 
    xa.append(xx) 
    ya.append(yy)'''

ax.plot(xa, ya, color='m', linestyle='', marker='.')

# 求出等式左边的矩阵A

matA=[]
for i in range(0,order+1):
    mat=[]
    for j in range(0+i,order+1+i):
        sumA=0
        for xx in xa:
            sumA=sumA+xx**j
        mat.append(sumA)
    matA.append(mat)
A=np.array(matA)

# 求出右边的等式B
matB=[]
for j in range(0,order+1):
    sumB=0
    for xx,yy in zip(xa,ya):
        sumB=sumB+xx**j*yy
    matB.append(sumB)
B=np.array(matB)
# 另外一种该方法求A
# 求出等式左边的矩阵A
A=[]
for xx in xa:
    matA = []
    for i in range(0,order+1):
        mat = []
        for j in range(0+i,order+1+i):
            mat.append(xx**j)
        matA.append(mat)
    A.append(matA)
# 求和
A=sum(np.array(A))

a=np.linalg.solve(A,B)
# 定义拟合函数
def fun_solve(x,a):
    y=0
    for i in range(len(a)):
        y+=a[i]*x**i
    return y

xxa= np.arange(-1,1.06,0.01)
yya=[]
for xxaa in xxa:
    yya.append(fun_solve(xxaa,a))

ax.plot(xxa,yya,color='g',linestyle='-',marker='')

参考博文：
https://blog.csdn.net/jairuschan/article/details/7517773/#commentBox
https://blog.csdn.net/einstein10147/article/details/79205109