An overview of gradient descent optimization algorithms

http://ruder.io/optimizing-gradient-descent/

Heap edtion 

Table of contents:

• Gradient descent variants
  • Batch gradient descent
  • Stochastic gradient descent
  • Mini-batch gradient descent
• Challenges
• Gradient descent optimization algorithms
  • Momentum
  • Nesterov accelerated gradient
  • Adagrad
  • Adadelta
  • RMSprop
  • Adam
  • AdaMax
  • Nadam
  • Visualization of algorithms
  • Which optimizer to choose?
• Parallelizing and distributing SGD
  • Hogwild!
  • Downpour SGD
  • Delay-tolerant Algorithms for SGD
  • TensorFlow
  • Elastic Averaging SGD
• Additional strategies for optimizing SGD
  • Shuffling and Curriculum Learning
  • Batch normalization
  • Early Stopping
  • Gradient noise
• Conclusion
• References

Gradient descent is one of the most popular algorithms to perform optimization and by far the most common way to optimize neural networks. At the same time, every state-of-the-art Deep Learning library contains implementations of various algorithms to optimize gradient descent (e.g. lasagne's, caffe's, and keras' documentation). These algorithms, however, are often used as black-box optimizers, as practical explanations of their strengths and weaknesses are hard to come by.

This blog post aims at providing you with intuitions towards the behaviour of different algorithms for optimizing gradient descent that will help you put them to use. We are first going to look at the different variants of gradient descent. We will then briefly summarize challenges during training. Subsequently, we will introduce the most common optimization algorithms by showing their motivation to resolve these challenges and how this leads to the derivation of their update rules. We will also take a short look at algorithms and architectures to optimize gradient descent in a parallel and distributed setting. Finally, we will consider additional strategies that are helpful for optimizing gradient descent.

Gradient descent is a way to minimize an objective function  J(θ) J(θ) parameterized by a model's parameters  θ∈Rd θ∈Rd by updating the parameters in the opposite direction of the gradient of the objective function  ∇θJ(θ) ∇θJ(θ) w.r.t. to the parameters. The learning rate  η η determines the size of the steps we take to reach a (local) minimum. In other words, we follow the direction of the slope of the surface created by the objective function downhill until we reach a valley. If you are unfamiliar with gradient descent, you can find a good introduction on optimizing neural networks here.

 Gradient descent variants

There are three variants of gradient descent, which differ in how much data we use to compute the gradient of the objective function. Depending on the amount of data, we make a trade-off between the accuracy of the parameter update and the time it takes to perform an update.

Batch gradient descent

Vanilla gradient descent, aka batch gradient descent, computes the gradient of the cost function w.r.t. to the parameters  θ θ for the entire training dataset:

θ=θ−η⋅∇θJ(θ) θ=θ−η⋅∇θJ(θ).

As we need to calculate the gradients for the whole dataset to perform just one update, batch gradient descent can be very slow and is intractable for datasets that don't fit in memory. Batch gradient descent also doesn't allow us to update our model online, i.e. with new examples on-the-fly.

In code, batch gradient descent looks something like this:

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad

For a pre-defined number of epochs, we first compute the gradient vector params_grad of the loss function for the whole dataset w.r.t. our parameter vector params. Note that state-of-the-art deep learning libraries provide automatic differentiation that efficiently computes the gradient w.r.t. some parameters. If you derive the gradients yourself, then gradient checking is a good idea. (See here for some great tips on how to check gradients properly.)

We then update our parameters in the direction of the gradients with the learning rate determining how big of an update we perform. Batch gradient descent is guaranteed to converge to the global minimum for convex error surfaces and to a local minimum for non-convex surfaces.

Stochastic gradient descent

Stochastic gradient descent (SGD) in contrast performs a parameter update for each training example  x(i) x(i) and label  y(i) y(i):

θ=θ−η⋅∇θJ(θ;x(i);y(i)) θ=θ−η⋅∇θJ(θ;x(i);y(i)).

Batch gradient descent performs redundant computations for large datasets, as it recomputes gradients for similar examples before each parameter update. SGD does away with this redundancy by performing one update at a time. It is therefore usually much faster and can also be used to learn online. 
SGD performs frequent updates with a high variance that cause the objective function to fluctuate heavily as in Image 1.

Image 1: SGD fluctuation (Source:  Wikipedia)

While batch gradient descent converges to the minimum of the basin the parameters are placed in, SGD's fluctuation, on the one hand, enables it to jump to new and potentially better local minima. On the other hand, this ultimately complicates convergence to the exact minimum, as SGD will keep overshooting. However, it has been shown that when we slowly decrease the learning rate, SGD shows the same convergence behaviour as batch gradient descent, almost certainly converging to a local or the global minimum for non-convex and convex optimization respectively. 
Its code fragment simply adds a loop over the training examples and evaluates the gradient w.r.t. each example. Note that we shuffle the training data at every epoch as explained in this section.

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

Mini-batch gradient descent

Mini-batch gradient descent finally takes the best of both worlds and performs an update for every mini-batch of  n n training examples:

θ=θ−η⋅∇θJ(θ;x(i:i+n);y(i:i+n)) θ=θ−η⋅∇θJ(θ;x(i:i+n);y(i:i+n)).

This way, it a) reduces the variance of the parameter updates, which can lead to more stable convergence; and b) can make use of highly optimized matrix optimizations common to state-of-the-art deep learning libraries that make computing the gradient w.r.t. a mini-batch very efficient. Common mini-batch sizes range between 50 and 256, but can vary for different applications. Mini-batch gradient descent is typically the algorithm of choice when training a neural network and the term SGD usually is employed also when mini-batches are used. Note: In modifications of SGD in the rest of this post, we leave out the parameters  x(i:i+n);y(i:i+n) x(i:i+n);y(i:i+n) for simplicity.

In code, instead of iterating over examples, we now iterate over mini-batches of size 50:

for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

Challenges

Vanilla mini-batch gradient descent, however, does not guarantee good convergence, but offers a few challenges that need to be addressed:

• Choosing a proper learning rate can be difficult. A learning rate that is too small leads to painfully slow convergence, while a learning rate that is too large can hinder convergence and cause the loss function to fluctuate around the minimum or even to diverge.

• Learning rate schedules [11] try to adjust the learning rate during training by e.g. annealing, i.e. reducing the learning rate according to a pre-defined schedule or when the change in objective between epochs falls below a threshold. These schedules and thresholds, however, have to be defined in advance and are thus unable to adapt to a dataset's characteristics [10].

• Additionally, the same learning rate applies to all parameter updates. If our data is sparse and our features have very different frequencies, we might not want to update all of them to the same extent, but perform a larger update for rarely occurring features.

• Another key challenge of minimizing highly non-convex error functions common for neural networks is avoiding getting trapped in their numerous suboptimal local minima. Dauphin et al. [19] argue that the difficulty arises in fact not from local minima but from saddle points, i.e. points where one dimension slopes up and another slopes down. These saddle points are usually surrounded by a plateau of the same error, which makes it notoriously hard for SGD to escape, as the gradient is close to zero in all dimensions.

Gradient descent optimization algorithms

In the following, we will outline some algorithms that are widely used by the deep learning community to deal with the aforementioned challenges. We will not discuss algorithms that are infeasible to compute in practice for high-dimensional data sets, e.g. second-order methods such as Newton's method.

Momentum

SGD has trouble navigating ravines, i.e. areas where the surface curves much more steeply in one dimension than in another [1], which are common around local optima. In these scenarios, SGD oscillates across the slopes of the ravine while only making hesitant progress along the bottom towards the local optimum as in Image 2.

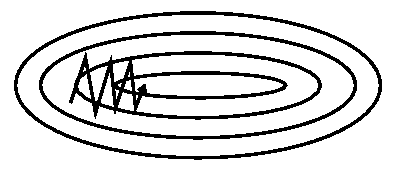Image 2: SGD without momentum

Image 3: SGD with momentum

Momentum [2] is a method that helps accelerate SGD in the relevant direction and dampens oscillations as can be seen in Image 3. It does this by adding a fraction  γ γ of the update vector of the past time step to the current update vector:

vtθ=γvt−1+η∇θJ(θ)=θ−vt vt=γvt−1+η∇θJ(θ)θ=θ−vt

Note: Some implementations exchange the signs in the equations. The momentum term  γ γ is usually set to 0.9 or a similar value.

Essentially, when using momentum, we push a ball down a hill. The ball accumulates momentum as it rolls downhill, becoming faster and faster on the way (until it reaches its terminal velocity if there is air resistance, i.e.  γ<1 γ<1). The same thing happens to our parameter updates: The momentum term increases for dimensions whose gradients point in the same directions and reduces updates for dimensions whose gradients change directions. As a result, we gain faster convergence and reduced oscillation.

Nesterov accelerated gradient

However, a ball that rolls down a hill, blindly following the slope, is highly unsatisfactory. We'd like to have a smarter ball, a ball that has a notion of where it is going so that it knows to slow down before the hill slopes up again.

Nesterov accelerated gradient (NAG) [7] is a way to give our momentum term this kind of prescience. We know that we will use our momentum term  γvt−1 γvt−1 to move the parameters  θ θ. Computing  θ−γvt−1 θ−γvt−1thus gives us an approximation of the next position of the parameters (the gradient is missing for the full update), a rough idea where our parameters are going to be. We can now effectively look ahead by calculating the gradient not w.r.t. to our current parameters  θ θ but w.r.t. the approximate future position of our parameters:

vtθ=γvt−1+η∇θJ(θ−γvt−1)=θ−vt vt=γvt−1+η∇θJ(θ−γvt−1)θ=θ−vt

Again, we set the momentum term  γ γ to a value of around 0.9. While Momentum first computes the current gradient (small blue vector in Image 4) and then takes a big jump in the direction of the updated accumulated gradient (big blue vector), NAG first makes a big jump in the direction of the previous accumulated gradient (brown vector), measures the gradient and then makes a correction (red vector), which results in the complete NAG update (green vector). This anticipatory update prevents us from going too fast and results in increased responsiveness, which has significantly increased the performance of RNNs on a number of tasks [8].

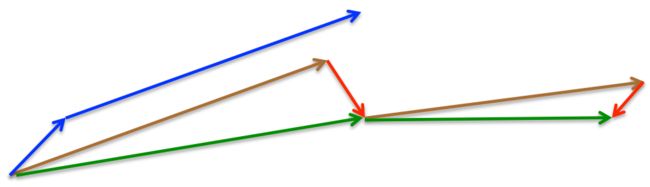Image 4: Nesterov update (Source:  G. Hinton's lecture 6c)

Refer to here for another explanation about the intuitions behind NAG, while Ilya Sutskever gives a more detailed overview in his PhD thesis [9].

Now that we are able to adapt our updates to the slope of our error function and speed up SGD in turn, we would also like to adapt our updates to each individual parameter to perform larger or smaller updates depending on their importance.

Adagrad

Adagrad [3] is an algorithm for gradient-based optimization that does just this: It adapts the learning rate to the parameters, performing larger updates for infrequent and smaller updates for frequent parameters. For this reason, it is well-suited for dealing with sparse data. Dean et al. [4] have found that Adagrad greatly improved the robustness of SGD and used it for training large-scale neural nets at Google, which -- among other things -- learned to recognize cats in Youtube videos. Moreover, Pennington et al. [5] used Adagrad to train GloVe word embeddings, as infrequent words require much larger updates than frequent ones.

Previously, we performed an update for all parameters  θ θ at once as every parameter  θi θi used the same learning rate  η η. As Adagrad uses a different learning rate for every parameter  θi θi at every time step  t t, we first show Adagrad's per-parameter update, which we then vectorize. For brevity, we set  gt,i gt,i to be the gradient of the objective function w.r.t. to the parameter  θi θi at time step  t t:

gt,i=∇θJ(θt,i) gt,i=∇θJ(θt,i).

The SGD update for every parameter  θi θi at each time step  t t then becomes:

θt+1,i=θt,i−η⋅gt,i θt+1,i=θt,i−η⋅gt,i.

In its update rule, Adagrad modifies the general learning rate  η η at each time step  t t for every parameter  θi θibased on the past gradients that have been computed for  θi θi:

θt+1,i=θt,i−ηGt,ii+ϵ−−−−−−√⋅gt,i θt+1,i=θt,i−ηGt,ii+ϵ⋅gt,i.

Gt∈Rd×d Gt∈Rd×d here is a diagonal matrix where each diagonal element  i,i i,i is the sum of the squares of the gradients w.r.t.  θi θi up to time step  t t [25], while  ϵ ϵ is a smoothing term that avoids division by zero (usually on the order of  1e−8 1e−8). Interestingly, without the square root operation, the algorithm performs much worse.

As  Gt Gt contains the sum of the squares of the past gradients w.r.t. to all parameters  θ θ along its diagonal, we can now vectorize our implementation by performing an element-wise matrix-vector multiplication  ⊙ ⊙between  Gt Gt and  gt gt:

θt+1=θt−ηGt+ϵ−−−−−√⊙gt θt+1=θt−ηGt+ϵ⊙gt.

One of Adagrad's main benefits is that it eliminates the need to manually tune the learning rate. Most implementations use a default value of 0.01 and leave it at that.

Adagrad's main weakness is its accumulation of the squared gradients in the denominator: Since every added term is positive, the accumulated sum keeps growing during training. This in turn causes the learning rate to shrink and eventually become infinitesimally small, at which point the algorithm is no longer able to acquire additional knowledge. The following algorithms aim to resolve this flaw.

Adadelta

Adadelta [6] is an extension of Adagrad that seeks to reduce its aggressive, monotonically decreasing learning rate. Instead of accumulating all past squared gradients, Adadelta restricts the window of accumulated past gradients to some fixed size  w w.

Instead of inefficiently storing  w w previous squared gradients, the sum of gradients is recursively defined as a decaying average of all past squared gradients. The running average  E[g2]t E[g2]t at time step  t t then depends (as a fraction  γ γ similarly to the Momentum term) only on the previous average and the current gradient:

E[g2]t=γE[g2]t−1+(1−γ)g2t E[g2]t=γE[g2]t−1+(1−γ)gt2.

We set  γ γ to a similar value as the momentum term, around 0.9. For clarity, we now rewrite our vanilla SGD update in terms of the parameter update vector  Δθt Δθt:

Δθtθt+1=−η⋅gt,i=θt+Δθt Δθt=−η⋅gt,iθt+1=θt+Δθt

The parameter update vector of Adagrad that we derived previously thus takes the form:

Δθt=−ηGt+ϵ−−−−−√⊙gt Δθt=−ηGt+ϵ⊙gt.

We now simply replace the diagonal matrix  Gt Gt with the decaying average over past squared gradients  E[g2]t E[g2]t:

Δθt=−ηE[g2]t+ϵ−−−−−−−−√gt Δθt=−ηE[g2]t+ϵgt.

As the denominator is just the root mean squared (RMS) error criterion of the gradient, we can replace it with the criterion short-hand:

Δθt=−ηRMS[g]tgt Δθt=−ηRMS[g]tgt.

The authors note that the units in this update (as well as in SGD, Momentum, or Adagrad) do not match, i.e. the update should have the same hypothetical units as the parameter. To realize this, they first define another exponentially decaying average, this time not of squared gradients but of squared parameter updates:

E[Δθ2]t=γE[Δθ2]t−1+(1−γ)Δθ2t E[Δθ2]t=γE[Δθ2]t−1+(1−γ)Δθt2.

The root mean squared error of parameter updates is thus:

RMS[Δθ]t=E[Δθ2]t+ϵ−−−−−−−−−√ RMS[Δθ]t=E[Δθ2]t+ϵ.

Since  RMS[Δθ]t RMS[Δθ]t is unknown, we approximate it with the RMS of parameter updates until the previous time step. Replacing the learning rate  η η in the previous update rule with  RMS[Δθ]t−1 RMS[Δθ]t−1 finally yields the Adadelta update rule:

Δθtθt+1=−RMS[Δθ]t−1RMS[g]tgt=θt+Δθt Δθt=−RMS[Δθ]t−1RMS[g]tgtθt+1=θt+Δθt

With Adadelta, we do not even need to set a default learning rate, as it has been eliminated from the update rule.

RMSprop

RMSprop is an unpublished, adaptive learning rate method proposed by Geoff Hinton in Lecture 6e of his Coursera Class.

RMSprop and Adadelta have both been developed independently around the same time stemming from the need to resolve Adagrad's radically diminishing learning rates. RMSprop in fact is identical to the first update vector of Adadelta that we derived above:

E[g2]tθt+1=0.9E[g2]t−1+0.1g2t=θt−ηE[g2]t+ϵ−−−−−−−−√gt E[g2]t=0.9E[g2]t−1+0.1gt2θt+1=θt−ηE[g2]t+ϵgt

RMSprop as well divides the learning rate by an exponentially decaying average of squared gradients. Hinton suggests  γ γ to be set to 0.9, while a good default value for the learning rate  η η is 0.001.

Adam

Adaptive Moment Estimation (Adam) [15] is another method that computes adaptive learning rates for each parameter. In addition to storing an exponentially decaying average of past squared gradients  vt vtlike Adadelta and RMSprop, Adam also keeps an exponentially decaying average of past gradients  mt mt, similar to momentum:

mtvt=β1mt−1+(1−β1)gt=β2vt−1+(1−β2)g2t mt=β1mt−1+(1−β1)gtvt=β2vt−1+(1−β2)gt2

mt mt and  vt vt are estimates of the first moment (the mean) and the second moment (the uncentered variance) of the gradients respectively, hence the name of the method. As  mt mt and  vt vt are initialized as vectors of 0's, the authors of Adam observe that they are biased towards zero, especially during the initial time steps, and especially when the decay rates are small (i.e.  β1 β1 and  β2 β2 are close to 1).

They counteract these biases by computing bias-corrected first and second moment estimates:

m^tv^t=mt1−βt1=vt1−βt2 m^t=mt1−β1tv^t=vt1−β2t

They then use these to update the parameters just as we have seen in Adadelta and RMSprop, which yields the Adam update rule:

θt+1=θt−ηv^t−−√+ϵm^t θt+1=θt−ηv^t+ϵm^t.

The authors propose default values of 0.9 for  β1 β1, 0.999 for  β2 β2, and  10−8 10−8 for  ϵ ϵ. They show empirically that Adam works well in practice and compares favorably to other adaptive learning-method algorithms.

AdaMax

The  vt vt factor in the Adam update rule scales the gradient inversely proportionally to the  ℓ2 ℓ2 norm of the past gradients (via the  vt−1 vt−1 term) and current gradient  |gt|2 |gt|2:

vt=β2vt−1+(1−β2)|gt|2 vt=β2vt−1+(1−β2)|gt|2

We can generalize this update to the  ℓp ℓp norm. Note that Kingma and Ba also parameterize  β2 β2 as