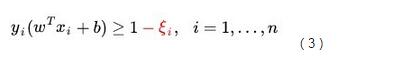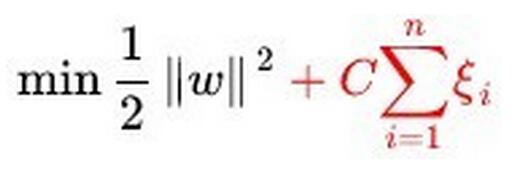机器学习:海量数据挖掘解决方案
文|纪传俊
文章开篇之前,先来点福利:(点击文字即可免费报名)
大数据时代里,互联网用户每天都会直接或间接使用到大数据技术的成果,直接面向用户的比如搜索引擎的排序结果,间接影响用户的比如网络游戏的流失用户预测、支付平台的欺诈交易监测等等。达观数据技术团队开发过智能文本内容审核系统、作弊监测系统、用户建模系统等多个基于大数据技术的应用系统。机器学习是大数据挖掘的一大基础,本文以机器学习为切入点,将达观在大数据技术实践时的一些经验与大家分享。
互联网的海量数据不可能靠人工一个个处理,只能依靠计算机批量处理。最初的做法是人为设定好一些规则,由机器来执行。比如明确指定计算机给男性、30岁的用户推送汽车广告。很明显如此粗略的规则不会有好效果,因为对人群的定位不够精确。要提高精度必须增加对用户的特征描述。但特征一多规则就很难制定,即使定下了规则也没法根据实际情况灵活变化。机器学习可以很好的解决以上问题,从一定程度上赋予了计算机以“学习”的能力,使得千人千面成为可能。
图 1 面对大量的特征,人工难以确定使用的规则
有监督机器学习技术
机器学习以统计学为理论基础,利用算法让机器具有类似人类一般的自动“学习”能力,即对已知的训练数据做统计分析从而获得规律,再运用规律对未知数据做预测分析。机器学习主要包含四大类别:有监督学习,无监督学习,半监督学习和增强学习。
有监督学习,顾名思义,是在“人类监督”下学习,要求训练数据既有特征也有目标,目标是人为设定好的。以文本分类为例,一篇文章的字、词、句、段是其特征(文本的内容是什么),文章的类别(时事、科技、娱乐等等)就是目标。训练集文章的类别是人为设定的,相当于明确告诉机器什么样的内容该属于什么类别,机器在此基础上总结规律。无监督学习就是数据只有特征没有目标,最常见的算法是聚类。聚类算法会把相似的样本聚集成一个子集,优点是数据无需人工标注,但缺点也很明显——无法给出子集的实际含义。半监督学习介于有监督学习和无监督学习之间,其训练集数据有一小部分是人工标注过的。增强学习强调基于环境而行动,在探索未知领域和遵从现有只是之间寻求平衡。
有监督学习的研究起步较早,方法比较成熟。在大多数应用场景中,我们希望机器输出的结果具有实际含义,比如文本分类就是让机器告诉我们一篇文章是时事还是科技类文章。这样的场景下有监督学习也更为适用。有监督学习主要包含回归分析和统计分类两大类算法。
回归分析——预估点击率的利器
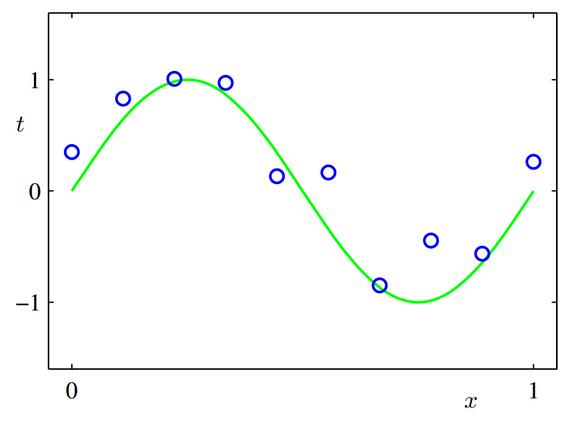
回归分析建模的是自变量和因变量之间的相关关系(如图2所示),在机器学习领域,自变量是样本的特征向量,因变量是预测值。回归分析最经典的应用场景是广告点击率(CTR)预估。简单而言,CTR预估是根据用户数据和广告数据,估计用户点击某个广告的可能性大小。我们假设用户数据+广告数据和广告点击率之间的关系符合某个分布,使用回归分析方法在已有点击数据上拟合出该分布。达观科技在线上预测时就把用户数据和广告数据作为输出传给拟合出的分布,得到用户点击该广告的概率值。
图 2 回归分析示意图
统计分类——被广泛应用的机器学习方法
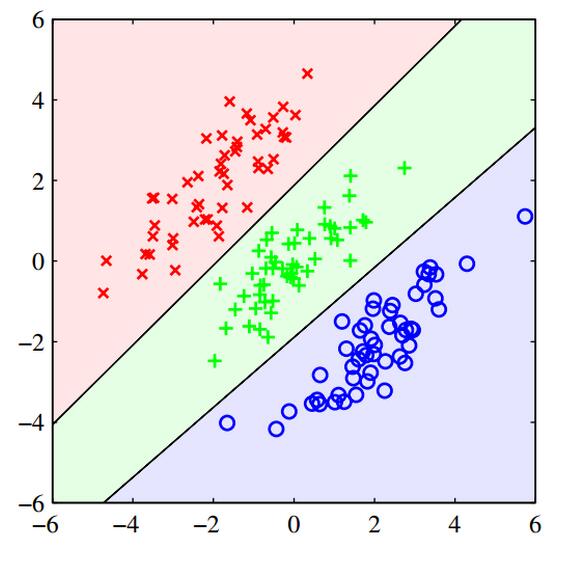
统计分类要解决的问题是,如何将一个样本点分到类别集合中的一个或多个类,比如图3所表示的就是将数据分为3个类。
图 3 统计分类示意图
现实场景中我们往往需要把数据分成不同的类别,以方便我们分析和使用,因而统计分类方法具有广阔的应用范围。达观数据团队开发的用户建模、内容审核系统、反作弊系统等都使用到了统计分类模型。比如反作弊系统,目的是区分用户行为是否作弊,抽象出来就是个分类问题:输入是用户的各种行为数据经过处理后得到的特征,输出只有两个类别——“作弊”和“非作弊”。接下来我就简单介绍一下最具代表性的分类算法——支持向量机(Support Vector Machine, SVM),一窥机器学习的工作原理。SVM绝不是入门级的机器学习算法,选择介绍它是因为,机器学习需要解决的数据线性不可分、过拟合等问题,SVM都给出了比较可靠的解决方案,借此我们也可以对机器学习有个大概的认识。
理想情况下SVM的理论模型
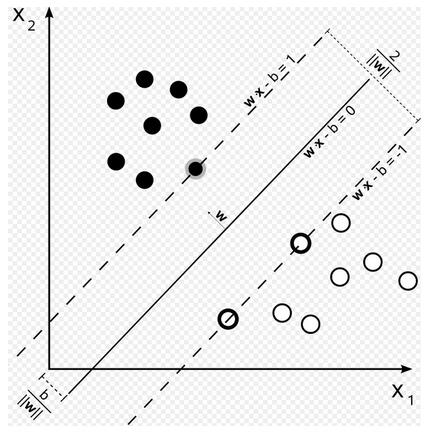
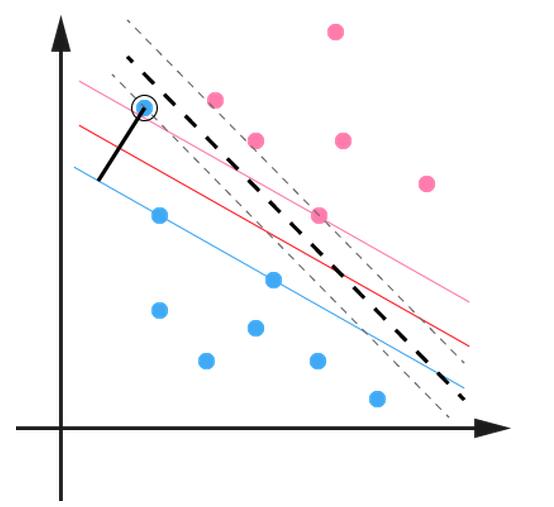
SVM针对分类问题的前提假设直观易懂,由此推演出的模型求解过程也是顺理成章一气呵成。我们通常先从最简单的情况入手,假设数据是线性可分的。SVM认为此时的最优分类面,是使得样本集到分类面的最小几何距离最大化的超平面,这个距离成为“间隔(margin)”。如图4所示,黑色实线就是最优分类面,两边两条虚线之间的几何距离就是此时的最优间隔。数据点离分类面越远,分类的置信度也越高。
图 4 SVM最优分类面示意图
SVM假设线性分类面的函数形式为
鉴于篇幅关系,我们略去推导过程。在最大化间隔的假设下,可以得到SVM的原目标函数为:
其中表示第i个样本的特征向量,是第i个样本的类标签,SVM令。由约束条件可知,样本点必然落在最优间隔的边缘(图4中虚线)上或外面,通过推导分析最终可以知道,只有落在间隔边缘上的少量数据点决定了分类面,这些样本被称为支持向量,而其他的点没有任何作用。这一特性大大节省了求解SVM的计算量。
线性不可分情况的处理
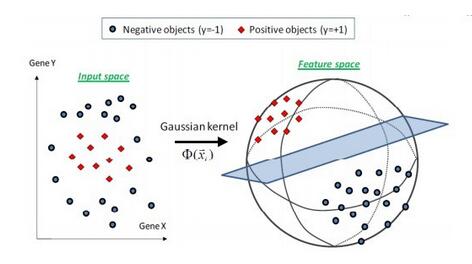
按照达观数据的经验,真实环境的问题往往是线性不可分的,数据采集的时候也不可避免的会引入噪声。应对这两种情况只需对原始SVM模型做有限的一点改进。针对数据线性不可分的情况,SVM通过引入核函数(Kernel Function)将数据映射到高维空间来解决,图5直观的表示了映射的过程。核函数实际上是两个数据点在高维空间中的内积。它先在原空间进行计算再将结果映射到高维空间,避免了先把数据点映射到高维空间再计算所可能导致的维数灾难问题。核函数可以从容的处理包括无限维在内的任何特征空间映射。
图 5 SVM核函数的作用原理图
SVM如何规避过拟合
过拟合(Overfitting)表现为在训练数据上模型的预测错误很低,在未知数据上预测错误却很高。图6的蓝色曲线代表训练错误,红色曲线代表真实错误,可以看到随着模型复杂度的升高,模型对训练数据的拟合程度越好(训练错误越低),但到了一定程度之后真实错误反而上升,即为过拟合。
图 6 过拟合
过拟合主要源于我们采集的训练样本带有噪声,有部分样本严重偏离其正常位置,统计学上称之为outlier。前面已经提到,决定SVM最优分类面的只是占少数的支持向量,如果碰巧这些支持向量中存在outlier,而我们又要求SVM尽可能完美的去拟合这样的数据,得到的分类面可能就会有问题。如图7所示,黑色加粗虚线代表最优分类面,带黑圈的蓝色数据点代表outlier。可以看到outlier严重偏离了正常蓝色数据点的位置,所在位置又恰巧使其成为了支持向量,导致了最终的分类面(深红色实线)严重偏离最优分类面。
图7 数据噪声对SVM的影响
解决办法非常简单而巧妙, Corinna Cortes与Vapnik为SVM引入了松弛变量(slack variable),将公式(2)的约束条件修改为:
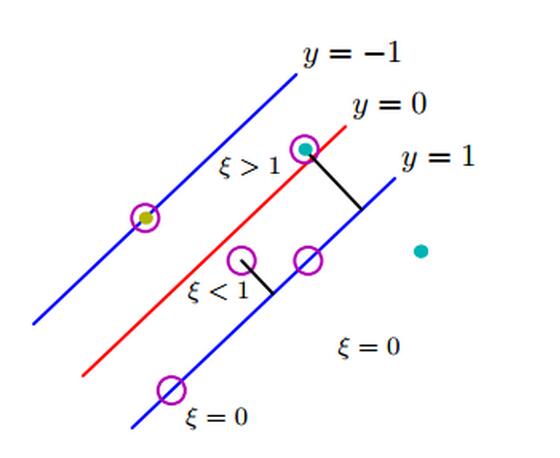
其中即为松弛变量。从图8可以看到,引入松弛变量即容忍了outlier的偏移量,抵消了outlier对分类面的负面影响。
图 8 松弛变量的作用
但容忍也不可以是无限制的,否则任意超平面都可以是“最优”超平面。因此公示(2)中的目标函数也需要相应的修改,限制松弛变量的总和尽量的小:
公示(4)可以理解为,在对outlier做出有限度的容忍情况下寻找使间隔最大化的最优超平面,至此才是一个能实际应用的完整SVM。如果想详细了解SVM的来龙去脉,推荐《An Introduction to Support Vector Machines and other kernel-based learning methods》(中文译本《支持向量机导论》,李国正翻译)。
达观数据运用机器学习技术的经验
经过长期的不断摸索,我们积累了不少让机器学习理论能真正实用的经验。机器学习的方法都各有特点,SVM也不是万能的算法,实际应用中应该根据具体情况选择合适的方法。选好方法,到获得我们预期的效果之间,还需要经过一番细心调校,调校的基础是对所选方法的数学模型的理解,以及对当前问题和数据的深入分析。
简单又不简单的参数调节
调参数是最基础的步骤,虽看似简单却也内有乾坤。不同模型可以调节的参数数量不同,可以采取“抓大放小”的原则,调节少数几个(数量最好控制在1到2个)影响最大的参数,否则参数的组合呈指数级增长会变得难以调节。
大多数模型都有一个控制过拟合的参数,据我们的经验来看,一般情况下这个参数对预测效果的好坏影响最大。对于SVM模型,前文提到过的限制松弛变量部分的C参数就起到控制过拟合的作用,调节C参数一般也能看到预测效果出现较大变化。此外,如果使用了高斯核函数将原始特征空间映射到无限维,那高斯核参数往往需要调节。因为太小的可以把任何数据都映射成线性可分,导致非常严重的过拟合问题。相反,太大会使得映射后的空间仍然是低维空间,起不到升维的效果。
交叉检验和AB测试
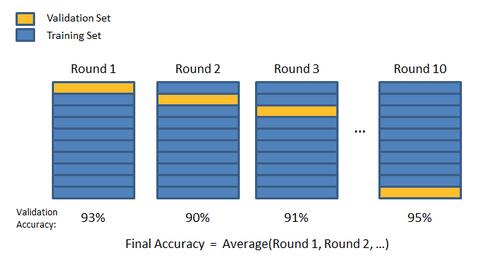
调参数需要用预测效果来比较还坏,有人可能会问,那该如何测试才能比较客观的检验参数甚至模型的有效性?我们的测试方法主要有两种:离线测试和在线测试。离线测试时我们只有训练数据,一般会采用学术界常用的交叉验证方法。如图9所示,我们将训练数据平均分为n份,在这n份数据上进行n次循环,每次取其中一份作为检验集(Validation Set),其他n-1份作为训练集(Training Set)。最后对n次预测的结果求平均,以平均得分来对比不同的参数和模型。n一般取5、10或者20。
图 9 交叉验证
离线测试得到满意的性能提升之后,就可以进行在线测试。离线测试效果好,并不意味着上线就能取得满意效果。在线测试采用工业界广泛使用的AB测试,首先我们会从线上切一小部分流量(B流量)给新模型、新参数,将效果和使用原先的模型和参数的主流量(A流量)进行对比,如果效果有所提升,再增加B流量的比例。测试通过了就可以全流量上线。
特征工程(feature engineering)的探讨
业界这么多年的实践经验已经证明,能给机器学习系统的性能带来较大提升的,不是换新模型或者调参数,而是特征工程,andrew ng也说过,“Applied machine learning” is basically feature engineering.”。机器学习只是提供了通用的算法,不可能根据不同的应用场景去调整自身的数学模型或算法。这就需要我们加入一些人工干预。
特征工程基于不同应用的领域知识对样本提取关键特征,让机器学习算法能够发挥出最优效果。相对而言特征工程是比较耗费人力的步骤,实际操作中也会遇到较多困难,解决办法只有一个:了解你的问题,了解你的数据。做反作弊检测的时候,我们是细致观察过作弊用户的行为数据,做过一些简单的统计分析。对作弊用户的行为模式有一定的概念,才能设计出有用的特征让预测效果达到要求。
非线性模型 V.S. 线性模型
进入大数据时代,我们面临的都是海量数据的处理问题。我们处理的大数据集合,在完成特征工程之后,通常得到的特征维数很高,上千万维的特征也不少见。在某些应用场景下,比如文本分类,当样本数量足够多、特征维数足够大的时候,我们发现非线性模型的效果并没有比线性模型高出多少,但计算效率明显差很多。这也是台湾林智仁教授及其团队继LIBSVM之后又推出了LIBLINEAR的原因,LIBLINEAR确实更符合当下大数据处理的要求:快速、高效、性能有保证。如果数据量较大特征维数较多,线性模型是不错的选择;一方面,线性模型可以在效果达到使用要求的前提下保证在线应用的及时响应,另一方面也节约了离线训练的计算时间,可以提高特征工程迭代的效率。
结语
大数据时代之下,如何从已经积累的数据中挖掘出“金矿”以提高企业效益,已日渐成为各行各业的普遍痛点。设想一下如果能让每个企业都用上大数据技术,我们整体的经济效率必将有明显的提升。达观数据科技非常愿意与所有企业分享我们的经验和能力,助力各个企业享受大数据技术的成果。