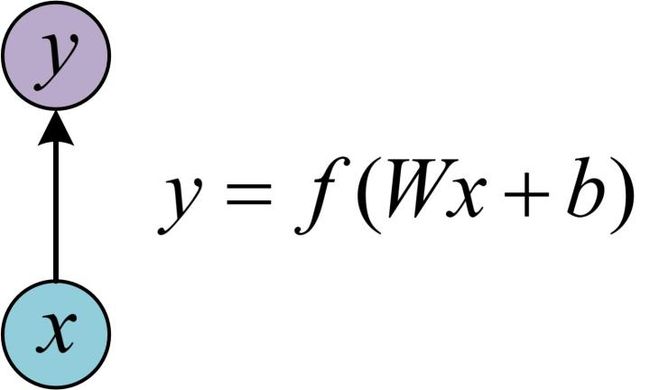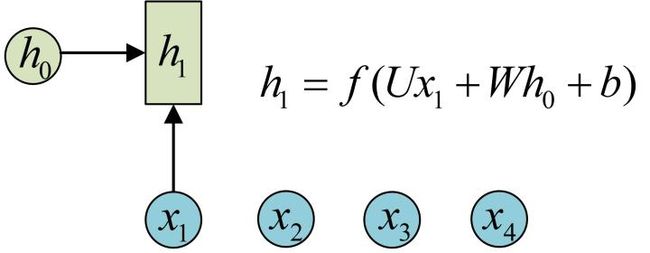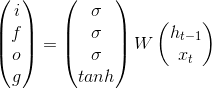RNN详解(Recurrent Neural Network)

一.概述

RNN用于处理序列数据。在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但是这种普通的神经网络对于很多问题却无能无力。例如，你要预测句子的下一个单词是什么，一般需要用到前面的单词，因为一个句子中前后单词并不是独立的。RNN之所以称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。理论上，RNN能够对任何长度的序列数据进行处理。但是在实践中，为了降低复杂性往往假设当前的状态只与前面的几个状态相关。

RNN重要特点：每一步的参数共享

二.RNN 多结构详解

RNN 有多种结构,如下所示：

1. one-to-one

                      

 最基本的单层网络，输入是x，经过变换Wx+b和激活函数f得到输出y。 

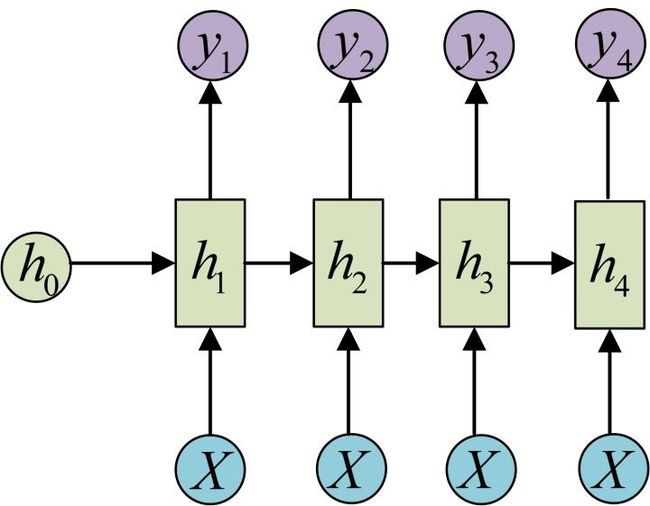
2. one-to-n

             

 还有一种结构是把输入信息X作为每个阶段的输入：

          

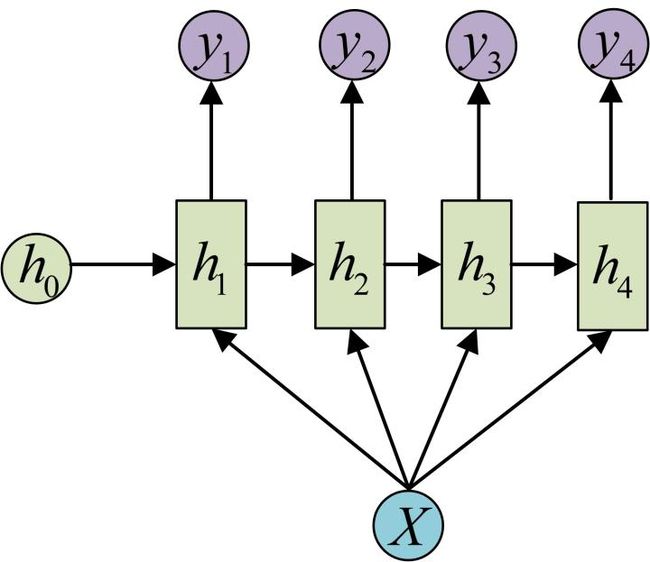
下图省略了一些X的圆圈，是一个等价表示：

                 

这种 one-to-n 的结构可以处理的问题有：

• 从图像生成文字（image caption），此时输入的X就是图像的特征，而输出的y序列就是一段句子，就像看图说话等
• 从类别生成语音或音乐等

3.n-to-n

最经典的RNN结构，输入、输出都是等长的序列数据。

                 

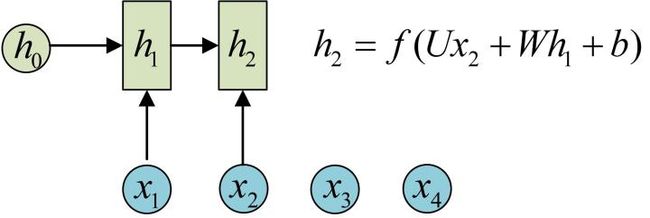
假设输入为X=(x1, x2, x3, x4)，每个x是一个单词的词向量。

为了建模序列问题，RNN引入了隐状态h（hidden state）的概念，h可以对序列形的数据提取特征，接着再转换为输出。先从h1的计算开始看：

                    

 h2的计算和h1类似。要注意的是，在计算时，每一步使用的参数U、W、b都是一样的，也就是说每个步骤的参数都是共享的，这是RNN的重要特点，一定要牢记。

                 

依次计算剩下来的（使用相同的参数U,W,b）：

           

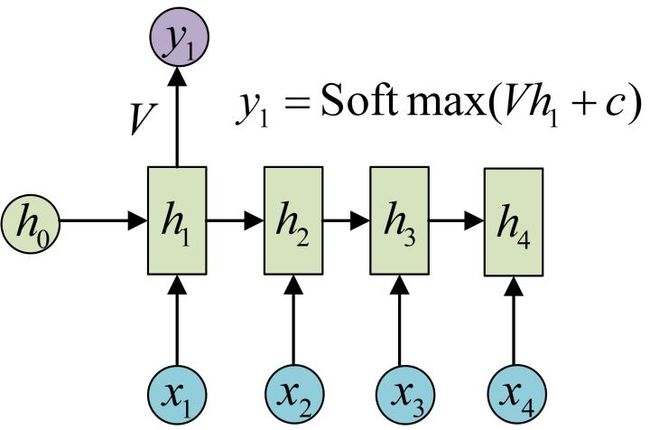
这里为了方便起见，只画出序列长度为4的情况，实际上，这个计算过程可以无限地持续下去。得到输出值的方法就是直接通过h进行计算：

                        

正如之前所说，一个箭头就表示对对应的向量做一次类似于f(Wx+b)的变换，这里的这个箭头就表示对h1进行一次变换，得到输出y1。

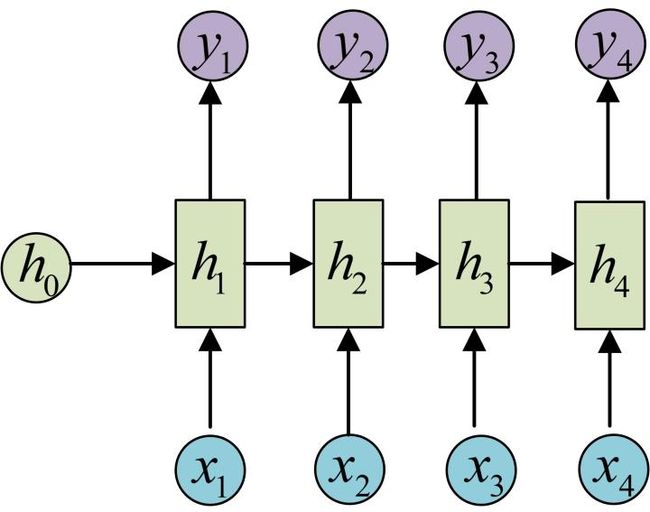
剩下的输出类似进行（使用和y1同样的参数V和c）：

                

这就是最经典的RNN结构，它的输入是x1, x2, …..xn，输出为y1, y2, …yn，也就是说，输入和输出序列必须要是等长的。由于这个限制的存在，经典RNN的适用范围比较小，但也有一些问题适合用经典的RNN结构建模，如：

• 计算视频中每一帧的分类标签。因为要对每一帧进行计算，因此输入和输出序列等长。
• 输入为字符，输出为下一个字符的概率。这就是著名的Char RNN（详细介绍请参考http://karpathy.github.io/2015/05/21/rnn-effectiveness/，Char RNN可以用来生成文章，诗歌，甚至是代码，非常有意思）。

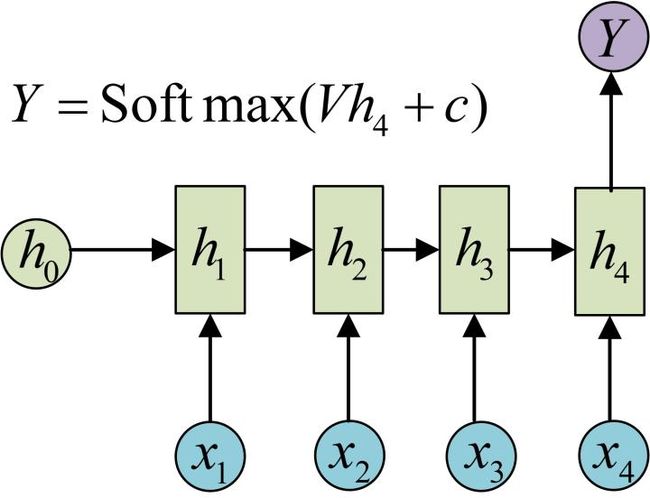
4.n-to-one

要处理的问题输入是一个序列，输出是一个单独的值而不是序列，应该怎样建模呢？实际上，我们只在最后一个h上进行输出变换就可以了：

                  

这种结构通常用来处理序列分类问题。如输入一段文字判别它所属的类别，输入一个句子判断其情感倾向，输入一段视频并判断它的类别等等。

5.Encoder-Decoder

n-to-m:

还有一种是 n-to-m，输入、输出为不等长的序列。

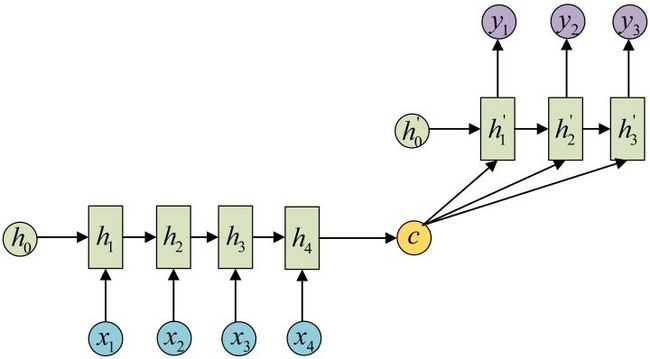
这种结构是Encoder-Decoder，也叫Seq2Seq，是RNN的一个重要变种。原始的n-to-n的RNN要求序列等长，然而我们遇到的大部分问题序列都是不等长的，如机器翻译中，源语言和目标语言的句子往往并没有相同的长度。为此，Encoder-Decoder结构先将输入数据编码成一个上下文语义向量c：

                   

语义向量c可以有多种表达方式，最简单的方法就是把Encoder的最后一个隐状态赋值给c，还可以对最后的隐状态做一个变换得到c，也可以对所有的隐状态做变换。

拿到c之后，就用另一个RNN网络对其进行解码，这部分RNN网络被称为Decoder。Decoder的RNN可以与Encoder的一样，也可以不一样。具体做法就是将c当做之前的初始状态h0输入到Decoder中：

               

 还有一种做法是将c当做每一步的输入：

                     

 Encoder-Decoder 应用

由于这种Encoder-Decoder结构不限制输入和输出的序列长度，因此应用的范围非常广泛，比如：

• 机器翻译：Encoder-Decoder的最经典应用，事实上这结构就是在机器翻译领域最先提出的。
• 文本摘要：输入是一段文本序列，输出是这段文本序列的摘要序列。
• 阅读理解：将输入的文章和问题分别编码，再对其进行解码得到问题的答案。
• 语音识别：输入是语音信号序列，输出是文字序列。

Encoder-Decoder 框架

Encoder-Decoder 不是一个具体的模型，是一种框架。

• Encoder：将 input序列 →转成→ 固定长度的向量
• Decoder：将 固定长度的向量 →转成→ output序列
• Encoder 与 Decoder 可以彼此独立使用，实际上经常一起使用

因为最早出现的机器翻译领域，最早广泛使用的转码模型是RNN。其实模型可以是 CNN /RNN /BiRNN /LSTM /GRU /…

Encoder-Decoder 缺点

• 最大的局限性：编码和解码之间的唯一联系是固定长度的语义向量c
• 编码要把整个序列的信息压缩进一个固定长度的语义向量c
• 语义向量c无法完全表达整个序列的信息
• 先输入的内容携带的信息，会被后输入的信息稀释掉，或者被覆盖掉
• 输入序列越长，这样的现象越严重，这样使得在Decoder解码时一开始就没有获得足够的输入序列信息，解码效果会打折扣

因此，为了弥补基础的 Encoder-Decoder 的局限性，提出了attention机制。

6.Attention Mechanism

注意力机制（attention mechanism）是对基础Encoder-Decoder的改良。Attention机制通过在每个时间输入不同的c来解决问题，下图是带有Attention机制的Decoder：

                   

每一个c会自动去选取与当前所要输出的y最合适的上下文信息。具体来说，我们用aij衡量Encoder中第j阶段的hj和解码时第i阶段的相关性，最终Decoder中第i阶段的输入的上下文信息 ci就来自于所有 hj 对 aij 的加权和。

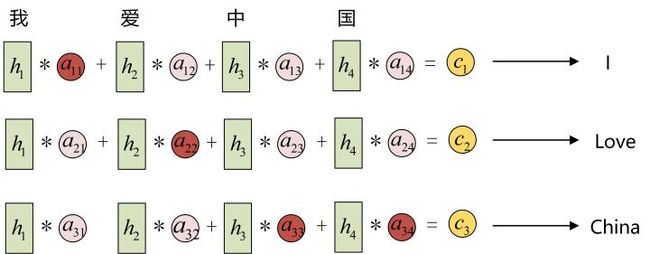
以机器翻译为例（将中文翻译成英文）：

                      

输入的序列是“我爱中国”，因此，Encoder中的h1、h2、h3、h4就可以分别看做是“我”、“爱”、“中”、“国”所代表的信息。在翻译成英语时，第一个上下文c1应该和 “我” 这个字最相关，因此对应的 a11 就比较大，而相应的 a12、a13、a14 就比较小。c2应该和“爱”最相关，因此对应的 a22 就比较大。最后的c3和h3、h4最相关，因此 a33、a34 的值就比较大。

至此，关于Attention模型，只剩最后一个问题了，那就是：这些权重 aij 是怎么来的？

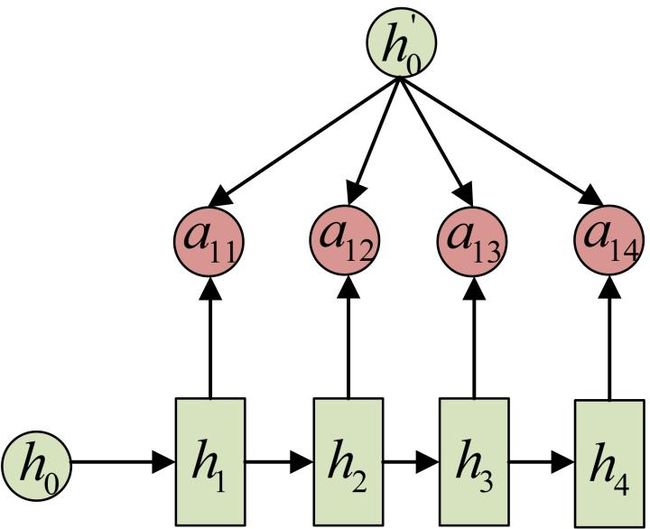
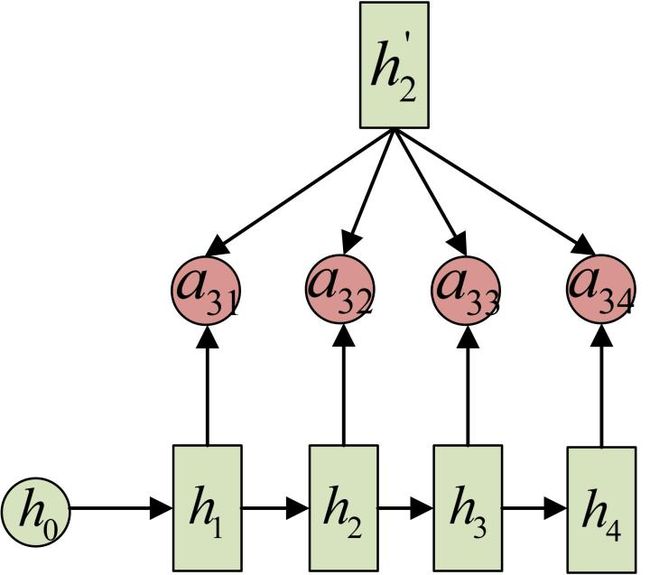
事实上，aij 同样是从模型中学出的，它实际和Decoder的第i-1阶段的隐状态、Encoder第j个阶段的隐状态有关。

同样还是拿上面的机器翻译举例， a1j 的计算（此时箭头就表示对h’和 hj 同时做变换）：

                  

 a2j 的计算：

                 

a3j 的计算：

                 

 以上就是带有Attention的Encoder-Decoder模型计算的全过程。

Attention 的优点：

• 在机器翻译时，让生词不只是关注全局的语义向量c，增加了“注意力范围”。表示接下来输出的词要重点关注输入序列种的哪些部分。根据关注的区域来产生下一个输出。
• 不要求编码器将所有信息全输入在一个固定长度的向量中。
• 将输入编码成一个向量的序列，解码时，每一步选择性的从序列中挑一个子集进行处理。
• 在每一个输出时，能够充分利用输入携带的信息，每个语义向量Ci不一样，注意力焦点不一样。

Attention 的缺点

• 需要为每个输入输出组合分别计算attention。50个单词的输出输出序列需要计算2500个attention。
• attention在决定专注于某个方面之前需要遍历一遍记忆再决定下一个输出是以什么。

Attention的另一种替代方法是强化学习，来预测关注点的大概位置。但强化学习不能用反向传播算法端到端的训练。

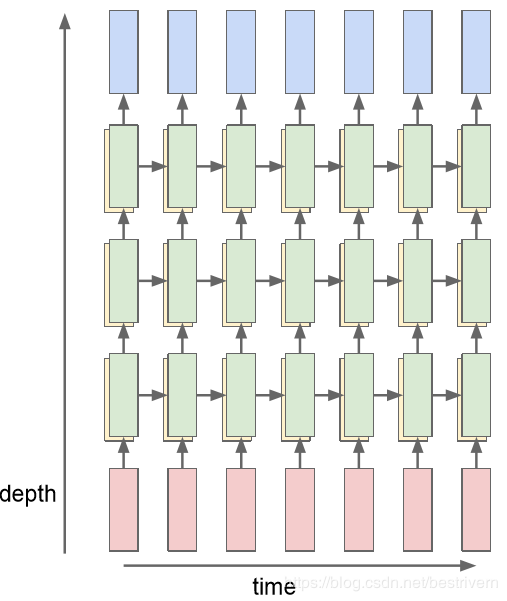
7.Multilayer RNNs

  RNNs也可以有多个隐层。

                                        

                                                                                      

                                                                                                 

三.RNN数学原理

给出一个典型的RNN:

                      

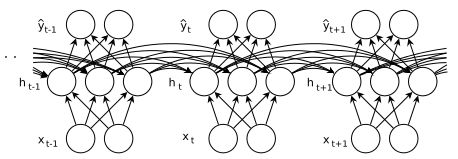
在图中：有一条单向流动的信息流是从输入单元到达隐藏单元的，与此同时另一条单向流动的信息流从隐藏单元到达输出单元。在某些情况下，RNNs会打破后者的限制，引导信息从输出单元返回隐藏单元，这些被称为“Back Projections”，并且隐藏层的输入还包括上一隐藏层的状态，即隐藏层内的节点可以自连也可以互连。（这实际上就是LSTM）

右侧为计算时便于理解记忆而产开的结构。简单说，x为输入层，o为输出层，s为隐含层，而t指第几次的计算；V,W,U为权重，其中计算第t次的隐含层状态时为： 
                                                            

实现当前输入结果与之前的计算挂钩的目的。

表达得更直观的图有： 

                                      

                                            

按照上图所示，可知道RNN网络前向传播过程中满足下面的公式：                                                                                                  
                                                           
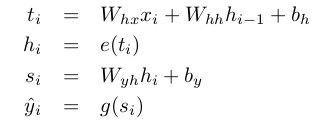
其代价函数可以是重构的误差： 
                                                                
也可以是交叉熵： 

                                     

 

四.LSTM

由于RNN模型如果需要实现长期记忆的话需要将当前的隐含态的计算与前n次的计算挂钩，即:                                                                                                        

那样的话计算量会呈指数式增长，导致模型训练的时间大幅增加，因此RNN模型一般不直接用来进行长期记忆计算。另外，传统RNN处理不了长期依赖问题，这是个致命伤。但LSTM解决了这个问题。

Long Short Term网络—— 一般就叫做 LSTM ——是一种 RNN 特殊的类型，可以学习长期依赖信息。LSTM 由 Hochreiter & Schmidhuber (1997) 提出，并在近期被 Alex Graves 进行了改良和推广。对于很多问题，LSTM 都取得相当巨大的成功，并得到了广泛的使用。

LSTM 通过刻意的设计来避免长期依赖问题。记住长期的信息在实践中是 LSTM 的默认行为，而非需要付出很大代价才能获得的能力！

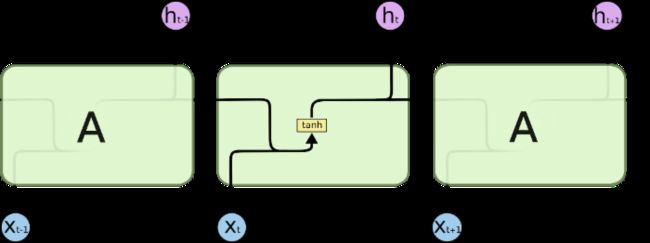
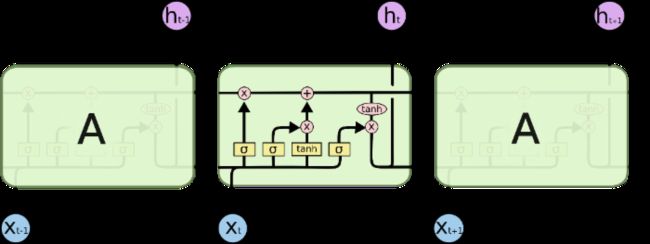
所有 RNN 都具有一种重复神经网络模块的链式的形式。在标准的RNN中，这个重复的模块只有一个非常简单的结构，例如一个 tanh层。 

                     

标准 RNN 中的重复模块包含单一的层。

LSTM 同样是这样的结构，但是重复的模块拥有一个不同的结构。不同于 单一神经网络层，这里是有四个，以一种非常特殊的方式进行交互。

                         

LSTM 中的重复模块包含四个交互的层。

                          

在上面的图例中，每一条黑线传输着一整个向量，从一个节点的输出到其他节点的输入。粉色的圈代表 pointwise 的操作，诸如向量的和，而黄色的矩阵就是学习到的神经网络层。合在一起的线表示向量的连接，分开的线表示内容被复制，然后分发到不同的位置。

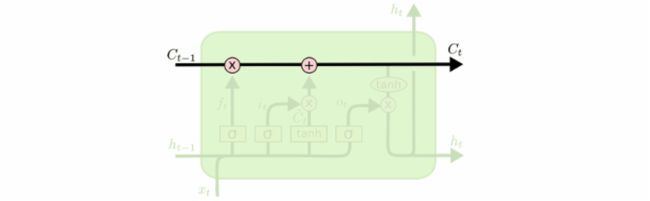
LSTM 的关键就是细胞状态（cell），水平线在图上方贯穿运行。细胞状态类似于传送带。直接在整个链上运行，只有一些少量的线性交互。信息在上面流传保持不变会很容易。 

                   

LSTM 有通过精心设计的称作为“门”的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个 sigmoid 神经网络层和一个 pointwise 乘法操作。 

Sigmoid 层输出 0 到 1 之间的数值，描述每个部分有多少量可以通过。0 代表“不许任何量通过”，1 就指“允许任意量通过”！

LSTM中有3个控制门：输入门，输出门，记忆门。

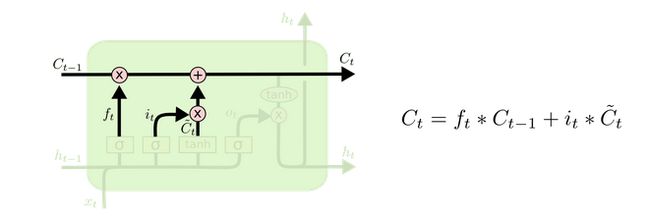
（1）forget gate：选择忘记过去某些信息：

                       

（2）input gate：记忆现在的某些信息：

                   

（3） 将过去与现在的记忆进行合并：

                       

（4）output gate：输出

                      

公式总结：