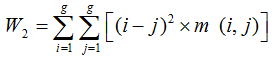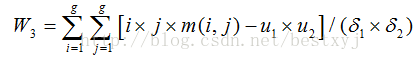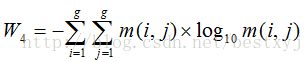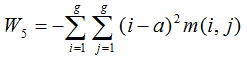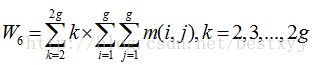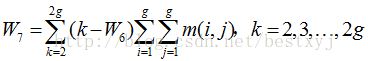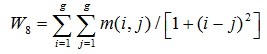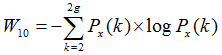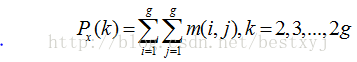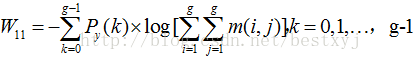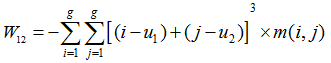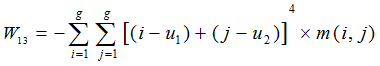灰度共生矩阵
灰度共生矩阵（gray level co-occurrence matrix,GLCM）是一种用来分析图像纹理特征的经典二阶统计法，大多适用于纹理分析。
这个角度还可以是0度，45度，135度。
上面是各个角度的位置分界线。
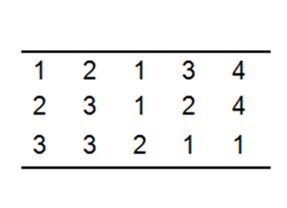
如下图的图像矩阵，90度方向的共生矩阵，只有
所以有（1,2）（2,3）（2,3）（3,3）（1,1）（1,2）（3,2）（2,1）（4,4）（4,1），就生成了灰度共生矩阵，其他角度同理可得。
图像的纹理特征不同，其共生矩阵也会明显不同。纹理比较细腻的区域，由于其像素对一般具有相同或相近的灰度，它的灰度共生矩阵中的值基本集中在主对角线，对于纹理粗糙的区域，其像素对灰度差异较大，灰度共生矩阵中的值则散布在各处。
灰度共生矩阵的特征参数
图像的灰度矩阵反映图像视觉信息，而灰度共生矩阵则反映灰度图像方向、相邻间隔、变化幅度的综合信息。通过统计灰度共生矩阵提取局部模式和排列规则，Haralick等人定义了14个用于纹理分析的灰度共生矩阵特征参数。
(1)角二阶矩(Angular Second Moment)
角二阶矩也称为能量，是灰度共生矩阵各元素的平方和。它是图像纹理灰度变化均匀性的度量，反映了图像灰度分布均匀程度和纹理粗细程度。如果共生矩阵的元素值相近，W1就小，纹理就细致，反之亦然。
(2)对比度(Contrast )
对比度是关于主对角线的惯性矩。它度量了矩阵值的分布情况和图像的局部变化。从数学角度看，共生阵中远离对角线元素的系数变大，W1随之变大。值越大表示纹理基元对比越强烈，沟纹越深，图像越清晰，纹理效果越明显，反之亦然。
(3)相关性(Correlation)
其中，
相关是度量空间灰度共生矩阵元素在行或列方向上的相似程度，是灰度线性关系的度量。当矩阵元素值均匀相等时，就大，反之亦然。如果图像的方向上方向性较强，而其他方向较弱，方向的将明显大于其他方向的。因此，可用来判断纹理的主方向。
(4)熵(Entropy)
熵代表了图像的信息量，是图像内容随机性的度量，能表征纹理的复杂程度。当图像无纹理时熵为0，满纹理时熵最大。从数学角度看，当共生矩阵中的元素近似相等时熵最大。
(5)方差 (Variance)
其中，a为m(i,j)的均值。
(6)均值和(Sum of Average)
均值和是图像区域内像素点平均灰度值的度量，反映图像的明暗深浅，适用于灰度图像。
(7)方差和(Sum of Variance)
方差、方差和反映纹理的周期大小，它们的值越大，表明纹理的周期越大。
(8)逆差矩(Inverse Difference Moment)，又称匀度
逆差矩又称为局部平稳，它是图像纹理局部变化的度量，反映纹理的规则程度。纹理越规则，匀度就越大，反之亦然。
(9)差的方差（Variance of Difference）
差的方差是邻近像素对中心像素灰度值差异的方差，对比越强烈，越大，反之亦然。
(10)和熵（Sum of Entropy）
其中 ，
。
(11)差熵（Difference of Entropy）
差熵与熵所代表的意义相近。
(12)聚类阴影（Shadow of Clustering）
其中 ，
。
(13)显著聚类（Prominence of Clustering）
其中 ， 
。
(14)最大概率（Maximal Probability）
上述公式中，g为图像的灰度级数。十四个统计特征中，能量、对比度、熵、匀度是最常用的四个统计特征参数。