编辑距离及问题延伸

编辑距离及问题延伸

由于最近在leetcode上刷题，这一阵又focus在了dynamic programming上面，动态规划一向就是面试的重点，而且题目难度普遍较大，难点并不在于像字符串数组中索引位置控制那种令人纠结的问题，更多是在思维上的深度，如果能够对问题进行很好的建模，代码通常会很简单，所以个人认为这类题目需要经常动笔写一写，从一些小例子出发寻求规律。

之前在上算法课的时候学习过动态规划的思想，而其中的编辑距离问题又是重中之重。恰好今天刷题的时候遇到了这类问题，所以动动笔，来总结一下。这是我的第一篇博客，希望能够开个好头。

编辑距离

又称Levenshtein距离（莱文斯坦距离也叫做Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作次数，如果它们的距离越大，说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。这三个操作的代价被认为是相同的，记为1。

这个距离通常被用来度量两个字符序列的相似程度，在长度一定的情况下，修改最小次数越多，两个序列的相似程度越小。举个简单的例子：两个字符串，str1="beast"，str2="seat"。如果统计这个修改次数，我们可以删除str1的'b' 和 's'，删除str2的's'，共三次操作，虽然我们也可以删除"bea"和"ea"，保留"st"，但是这样的操作就需要5次，并不是最经济的。

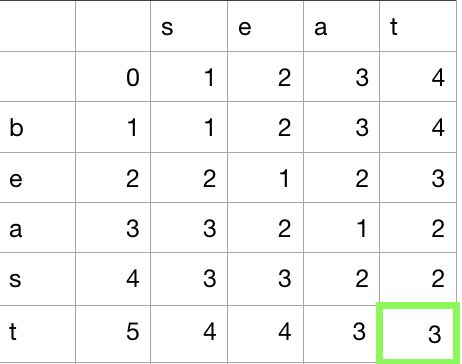
这个问题我们可以简化成一张二维表，最终右下角的结果就是使得两个字符串相等所用的最小步骤。

如何理解这个问题呢？

在这个二维矩阵中，对于每一个点 (i, j) ，我们可以做如下的理解：

它可以由 (i, j - 1) 和 (i - 1, j) 通过增加一个字符或者删除一个字符等到，同时也可以由 (i - 1, j - 1)处的字符通过更新操作得到。对于(i, j) 位置的操作步数而言，(i - 1, j) , (i, j - 1) , (i - 1, j - 1)这三个位置已经保证了实现之前子字符串相等状态所做处理的最优情况。而当前的最优处理步数可以由以下的递推关系式得出：

dp[i][j] = min(min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1] + temp)

其中，temp = 0 当 str1[i] == str2[j]（当前两个字符相同）说明不用update， temp = 1 当 str1[i] != str2[j]（当前两个字符不同），也就是说要触发一次update操作。

这个公式的含义是当前最优的处理操作数之可能来自三种情况，添加一个字符，删除一个字符，或者更新一个字符，我们要考察哪种情况使得当前操作次数最少。

我们以一个具体的例子来分析算法执行的过程：

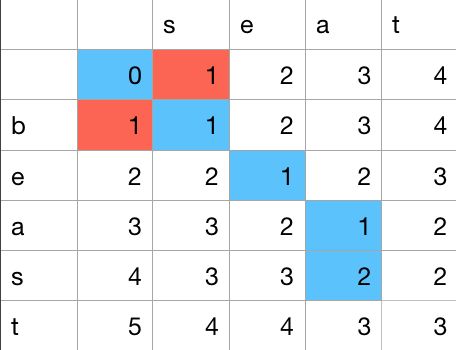
先观察左上角2*2的矩阵，0 代表刚开始两个字符串都是空的，(0, 1) 代表一个字符串为"s",另一个为空，此时，如果希望两个字符串相同，要么删除's'，要么对空字符串追加's'，都要进行一次操作。同理，(1, 0)位置是要么删除'b'，要么对空字符串追加'b'。也是一次操作。而对于(1, 1)位置而言，就是要考虑"s"和"b"的转化操作，很明显，如果通过增删的方式，需要执行两次，删除's'，追加'b'，或者删除'b'，追加's'。而如果通过更新操作，由于两个字符不同，需要更新一次，再加上之前的更新次数0，所以很明显最经济的方式是通过一次更新实现。符合递推公式。

接着，我们看蓝色的路径，到位置(4, 3)，看过程是如何进行的，此时的子问题是"sea" 和 "beas"，刚开始是对's'和'b'的一次更新，所以走对角线，之后，"ea"都是相同的，向右下移动两次，最后多出来的's'需要增删操作，所以是走的垂直路径。这一系列操作的结果和蓝色路径完全吻合。

算法实现

接下来，我们继续讨论下算法实现的步骤

STEP1 ：首先，建立动态规划表，dp[str1.length() + 1][str2.length() + 1]，加1的目的是字符串可以为空。

STEP2 : 接着，我们对 dp[0][i] 和 dp[i][0] 赋初值 i++;

STEP3 : 利用递推公式计算矩阵中的每个值，最终右下角的值就是最终结果。

具体代码实现如下：

class Solution72 {
    public int minDistance(String word1, String word2) {
    	if(word1.length() == 0) return word2.length();
    	if(word2.length() == 0) return word1.length();
        int len1 = word1.length();
        int len2 = word2.length();
        int[][] dp = new int[len1 + 1][len2 + 1];
        for(int i = 0 ; i < dp.length ; i++) dp[i][0] = i;
        for(int i = 0 ; i < dp[0].length ; i++) dp[0][i] = i;
        for(int i = 1 ; i < dp.length ; i++){
        	for(int j = 1 ; j < dp[0].length ; j++){
        		int temp = word1.charAt(i - 1) == word2.charAt(j - 1) ? 0 : 1;
        		dp[i][j] = Math.min(dp[i - 1][j - 1] + temp, Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
        	}
        }
        return dp[len1][len2];
    }
}

问题延伸

在leetcode还有一些延伸出来的问题，但是核心思想都是动态规划，完全可以按照编辑距离计算的方式来处理。

上面这道题是改变了编辑距离的处理方式，只允许删除操作（不能插入和更新），问我们最少通过多少步操作能够处理成相等的字符串。

实际上，我们应该清楚，如果允许删除，插入操作自然可以不用考虑，因为二者互为逆操作，而且代价相同。而更新操作可以看成是先删除旧的，再插入新的，所以实际上是删除操作代价的二倍。从这个角度看，我们只需要对递推关系式少做修改即可。如下：

 dp[i][j] = min(min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1] + temp)

其中，temp = 0 if(两个字符串当前的字符)相同，temp = 2 if (两个字符串当前的字符不同)

代码如下：

class Solution583 {
    public int minDistance(String word1, String word2) {
 	if(word1.length() == 0) return word2.length();
    	if(word2.length() == 0) return word1.length();
        int len1 = word1.length();
        int len2 = word2.length();
        int[][] dp = new int[len1 + 1][len2 + 1];
        for(int i = 0 ; i < dp.length ; i++) dp[i][0] = i;
        for(int i = 0 ; i < dp[0].length ; i++) dp[0][i] = i;
        for(int i = 1 ; i < dp.length ; i++){
        	for(int j = 1 ; j < dp[0].length ; j++){
        		int temp = word1.charAt(i - 1) == word2.charAt(j - 1) ? 0 : 2;//此处做了修改 1->2
        		dp[i][j] = Math.min(dp[i - 1][j - 1] + temp, Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
        	}
        }
        return dp[len1][len2];
    }
}

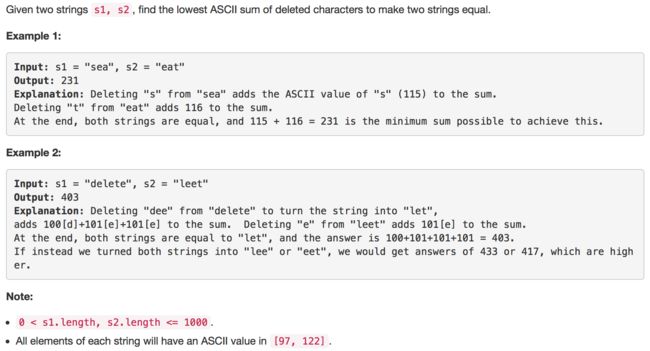
接下来的一道题改动略大，但是思路基本不变，题目如下：

这道题要求的不是删除的步数最小而是删除的字符的ascii总和最小，所以在每步递推的时候就不是计算哪种方式的步数少，而是计算如果删除当前字符所带来的ascii码增长的代价。所以，我们要对之前的程序范式作出更多的修改。

修改1： 赋初值的第一行，第一列是ascii码的累加和

修改2：递推关系式

 dp[i][j] = min(dp[i - 1][j - 1] + temp, min(dp[i][j - 1] + s2[j - 1], dp[i - 1][j] + s1[i - 1]));

当前字符相等时，temp = 0；当前字符不相等时，temp = s1[i - 1] + s2[j - 1]，删除两个当前字符。

具体代码如下：

class Solution712 {
    public int minimumDeleteSum(String s1, String s2) {
 		if(s1.length() == 0) return s2.length();
 		if(s2.length() == 0) return s1.length();
 		int[][] dp = new int[s1.length() + 1][s2.length() + 1];
 		for(int i = 1 ; i <= s1.length() ; i++) dp[i][0] = dp[i - 1][0] + s1.charAt(i - 1);
 		for(int j = 1 ; j <= s2.length() ; j++) dp[0][j] = dp[0][j - 1] + s2.charAt(j - 1);
 		for(int i = 1 ; i < dp.length ; i++){
 			for(int j = 1 ; j < dp[0].length ; j++){
 				int temp = s1.charAt(i - 1) == s2.charAt(j - 1) ? 0 : s1.charAt(i - 1) + s2.charAt(j - 1);
 				dp[i][j] = Math.min(dp[i - 1][j - 1] + temp, Math.min(dp[i][j - 1] + s2.charAt(j - 1), dp[i - 1][j] + s1.charAt(i - 1)));
 			}
 		}
 		return pd[s1.length()][s2.length()];
    }
}

以上是我个人今天刷题的总结，动态规划算法的学习需要不断的积累，很少说有几种通法就能够搞定所有问题，这与数据结构相关的问题截然不同，比如说二叉树问题，掌握分治递归思想（单层递归，双重递归），以及二叉树的dfs(preOrder, inOrder, postOrder)和bfs(队列)，就能解决百分之八十的问题。

千里之行，始于足下。希望能够对写博客产产生兴趣