线性代数1-向量和向量空间
同步于Buracag的博客;音尘杂记
后续几篇笔记主要想回顾整理一下需要用到的数学基础知识,主要包括了线性代数、微积分、概念论、数学优化和信息论等内容。相对比较基础,权当复习回顾完善整个知识体系结构。错误之处,还望诸君不吝指教。
文章目录
- 1. 向量
- 2. 向量空间
- 3. 常见的向量
- 4. 范数
1. 向量
标量(Scalar)是一个实数,只有大小,没有方向。而向量(Vector)是由一组实数组成的有序数组,同时具有大小和方向。例,一个n维向量a 是由n个有序实数组成,表示为:
(1.1) a = [ a 1 , a 2 , . . . , a n ] , a = [a_1, a_2, ..., a_n], \tag{1.1} a=[a1,a2,...,an],(1.1)
其中 a i a_i ai称为向量a的第 i i i个分量,或第 i i i维。向量符号通常用黑体小写字母 a , b , c a, b, c a,b,c或小写希腊字母 α , β , γ \alpha,\beta, \gamma α,β,γ 等来表示。
2. 向量空间
向量空间(Vector Space),也称线性空间(Linear Space),是指由向量组成的集合,并满足以下两个条件:
-
向量加法:向量空间 V V V中的两个向量a和b,它们的和a + b也属于空间 V V V;
-
标量乘法:向量空间 V V V中的任一向量a和任一标量 c c c,它们的乘积 c ⋅ a c · a c⋅a也属于空间 V V V。
欧氏空间 一个常用的线性空间是欧氏空间(Euclidean Space)。一个欧氏空间表示通常为 R n \mathbb{R}^n Rn,其中n为空间维度(Dimension)。欧氏空间中向量的加法和标量乘法定义为:
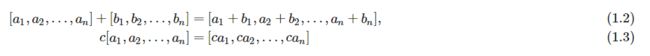
其中 a , b , c ∈ R a, b, c \in{\mathbb{R}} a,b,c∈R为一个标量。
线性子空间 向量空间 V V V的线性子空间 U U U是 V V V的一个子集,并且满足向量空间的条件(向量加法和标量乘法)。
线性无关 线性空间 V V V中的一组向量 v 1 , v 2 , . . . , v n {v_1, v_2, ... , v_n} v1,v2,...,vn,如果对任意的一组标量 λ 1 , λ 2 , . . . , λ n \lambda_1, \lambda_2, ... , \lambda_n λ1,λ2,...,λn,满足 λ 1 v 1 + λ 2 v 2 + ⋅ . . . + λ n v n = 0 \lambda_1v_1 + \lambda_2v_2 + ·... + \lambda_nv_n = 0 λ1v1+λ2v2+⋅...+λnvn=0,则必然 λ 1 = λ 2 = . . . = λ n = 0 \lambda_1 = \lambda_2 = ... =\lambda_n = 0 λ1=λ2=...=λn=0,那么 v 1 , v 2 , . . . , v n {v_1, v_2, ... , v_n} v1,v2,...,vn是线性无关的,也称为线性独立的。
基向量 向量空间 V V V的基(Base) B = e 1 , e 2 , . . . , e n B = {e_1, e_2, ... , e_n} B=e1,e2,...,en 是 V V V的有限子集,其元素之间线性无关。向量空间 V V V所有的向量都可以按唯一的方式表达为 B B B中向量的线性组合。对任意 v ∈ V v \in V v∈V,存在一组标量 ( λ 1 , λ 2 , . . . , λ n ) (\lambda_1, \lambda_2, ... , \lambda_n) (λ1,λ2,...,λn) 使得:
(1.4) v = λ 1 e 1 + λ 2 e 2 + . . . + λ n e n v = \lambda_1e_1 + \lambda_2e_2 + ... + \lambda_ne_n \tag{1.4} v=λ1e1+λ2e2+...+λnen(1.4)
其中基 B B B中的向量称为基向量(Base Vector)。如果基向量是有序的,则标量 ( λ 1 , λ 2 , . . . , λ n ) (\lambda_1, \lambda_2, ... , \lambda_n) (λ1,λ2,...,λn) 称为向量 v v v关于基 B B B的坐标(Coordinates)。
n维空间 V V V的一组标准基(Standard Basis)为:

向量空间 V V V中的任一向量 v = [ v 1 , v 2 , . . . , v n ] v = [v_1, v_2, ... , v_n] v=[v1,v2,...,vn]可以唯一的表示为:
(1.9) [ v 1 , v 2 , . . . , v n ] = v 1 e 1 + v 2 e 2 + . . . + v n e n , [v_1, v_2, ... , v_n] = v_1e_1 + v_2e_2 + ... + v_ne_n, \tag{1.9} [v1,v2,...,vn]=v1e1+v2e2+...+vnen,(1.9)
其中 v 1 , v 2 , . . . , v n v_1, v_2, ... , v_n v1,v2,...,vn也称为向量 v v v的笛卡尔坐标(Cartesian Coordinate)。向量空间中的每个向量可以看作是一个线性空间中的笛卡儿坐标。
内积** 一个n维线性空间中的两个向量 a a a和 b b b,其内积为:
(1.10) ⟨ a , b ⟩ = ∑ i = 1 n a i b i , ⟨a, b⟩ = \sum_{i=1}^{n}a_ib_i, \tag{1.10} ⟨a,b⟩=i=1∑naibi,(1.10)
正交 如果向量空间中两个向量的内积为0,则它们正交(Orthogonal)。如果向量空间中一个向量 v v v与子空间 U U U中的每个向量都正交,那么向量 v v v和子空间 U U U正交。
3. 常见的向量
全0向量指所有元素都为0的向量,用0表示。全0向量为笛卡尔坐标系中的原点。
全1向量指所有值为1的向量,用1表示。
one-hot向量为有且只有一个元素为1,其余元素都为0 的向量。one-hot向量是在数字电路中的一种状态编码,指对任意给定的状态,状态寄存器中只有1位为1,其余位都为0。
4. 范数
范数(Norm)是一个表示向量“长度”的函数,为向量空间内的所有向量赋予非零的正长度或大小。对于一个n维向量v,一个常见的范数函数为 ℓ p \ell_p ℓp范数
(1.11) ℓ p ( v ) = ∥ v ∥ p = ( ∑ i = 1 n ∣ v i ∣ p ) 1 / p , \ell_p(v) = \parallel v \parallel_p = {(\sum_{i=1}^{n}|v_i|^p)}^{1/p}, \tag{1.11} ℓp(v)=∥v∥p=(i=1∑n∣vi∣p)1/p,(1.11)
其中 p ≥ 0 p \geq 0 p≥0为一个标量的参数。常见的 p p p的取值有1,2, ∞ \infty ∞等。
ℓ 1 \ell_1 ℓ1范数 , p = 1 p = 1 p=1
(1.12) ℓ 1 ( v ) = ∑ i = 1 n ∣ v i ∣ , \ell_1(v) = \sum_{i=1}^{n}|v_i|, \tag{1.12} ℓ1(v)=i=1∑n∣vi∣,(1.12)
ℓ 2 \ell_2 ℓ2范数 , p = 2 p = 2 p=2
(1.13) ℓ 2 ( v ) = ∑ i = 1 n ∣ v i ∣ 2 = v T v , \ell_2(v) = \sqrt{\sum_{i=1}^{n}|v_i|^2} = \sqrt{v^Tv}, \tag{1.13} ℓ2(v)=i=1∑n∣vi∣2=vTv,(1.13)
ℓ 2 \ell_2 ℓ2范数又称为Euclidean范数或者Frobenius范数。从几何角度,向量也可以表示为从原点出发的一个有向线段,其 ℓ 2 \ell_2 ℓ2范数为线段的长度,也常称为向量的模。
ℓ ∞ \ell_{\infty} ℓ∞**范数 **, p = ∞ p = \infty p=∞,表示为各个元素的最大绝对值
(1.14) ℓ ∞ ( v ) = ∣ ∣ v ∣ ∣ ∞ = m a x { v 1 , v 2 , . . . , v n } , \ell_{\infty}(v) = ||v||_{\infty} = max\{v_1,v_2, ..., v_n\}, \tag{1.14} ℓ∞(v)=∣∣v∣∣∞=max{v1,v2,...,vn},(1.14)
主要参考https://github.com/nndl/nndl.github.io