推荐系统笔记7-Field-aware Factorization Machines for CTR Prediction
本文介绍Field-aware Factorization Machines for CTR Prediction,简称为FFM,其原文Paper传送门。
摘要
计算广告中CTR预估有着很重要的作用,其中二阶映射的FM常被使用,但提出的FFM在比赛中优于FM,因此引出FFM;
一、介绍
通常用LR处理分类问题,其模型是用来解决如下最优化问题:
min w λ 2 ∥ w ∥ 2 2 + ∑ i = 1 m log ( 1 + exp ( − y i ϕ L M ( w , x i ) ) ) \mathop {\min }\limits_w {\lambda \over 2}{\left\| w \right\|_2}^2 + \sum\limits_{i = 1}^m {\log (1 + \exp ( - {y_i}{\phi _{LM}}(w,{x_i})))} wmin2λ∥w∥22+i=1∑mlog(1+exp(−yiϕLM(w,xi)))
在LR中 ϕ ( w , x ) = w x \phi(w,x)=wx ϕ(w,x)=wx且 λ \lambda λ是正则化参数;其余的介绍同以前文章的介绍,就不展开叙述了,下面具体介绍FFM模型原理;
二、POLY2 和 FM模型
论文 “Training and testing low-degree polynomial data mappings via linear SVM" 提出二阶映射可以有效捕捉特征信息,其Poly2模型如下(为了偷懒,就直接截图了):
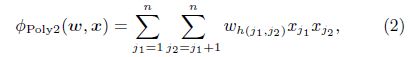
其中 h ( j 1 , j 2 ) h(j_1,j_2) h(j1,j2)是一个将 j 1 和 j 2 j_1和j_2 j1和j2编码到自然数的函数,其时间复杂度为 O ( n ˉ 2 ) O({{\bar n}^2}) O(nˉ2), n ˉ {\bar n} nˉ是每个实例平均的非0元素个数;
FM是一个对每个特征学习隐层向量的模型,假设每个特征映射为k维隐层向量,其计算公式如下:
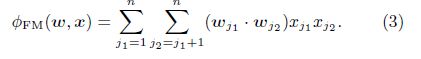
变量的数目是 n × k n\times k n×k,所以直接计算的时间复杂度是 O ( n ˉ 2 k ) O({{\bar n}^2k}) O(nˉ2k),重写上面的公式为: ϕ F M ( w , x ) = 1 2 ∑ j = 1 n ( s − w j x j ) ⋅ w j x j {\phi _{FM}}(w,x) = {1 \over 2}\sum\limits_{j = 1}^n {(s - {w_j}{x_j}) \cdot {w_j}{x_j}} ϕFM(w,x)=21j=1∑n(s−wjxj)⋅wjxj其中 s = ∑ j = 1 n w j x j s = \sum\limits_{j = 1}^n {{w_j}{x_j}} s=j=1∑nwjxj,此时时间复杂度变为 O ( n ˉ k ) O({{\bar n}k}) O(nˉk);为什么FM要优于Poly2呢?见该文章开头部分。
三、 FFM
FFM引进了field的概念,如下表所示:
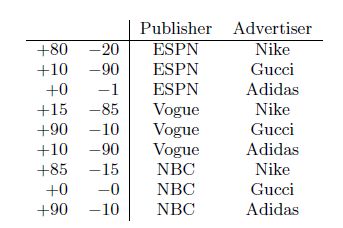
可以分为两个field,其中Publisher包含ESPN、Vogue、NBC,Advertiser包含Nike,Adidas等;FFM就是FM的一个变种,利用了上述field的信息;为了解释FFM,考虑下面一个例子:
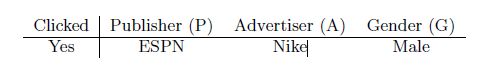
对于FM来说, ϕ ( w , x ) = w E S P N . w N i k e + w E S P N . w M a l e + w M a l e . w N i k e \phi(w,x)=w_{ESPN}.w_{Nike}+w_{ESPN}.w_{Male}+w_{Male}.w_{Nike} ϕ(w,x)=wESPN.wNike+wESPN.wMale+wMale.wNike,其中 w E S P N w_{ESPN} wESPN可以通过 w E S P N . w N i k e 和 w E S P N . w M a l e w_{ESPN}.w_{Nike}和w_{ESPN}.w_{Male} wESPN.wNike和wESPN.wMale来学习出它的向量,但是有个问题是,Male和Nike是不同的field,可能存在不同,所以FFM的公式定义为: ϕ ( w , x ) = w E S P N , A . w N i k e , P + w E S P N , G . w M a l e , P + w M a l e , A . w N i k e , G \phi(w,x)=w_{ESPN,A}.w_{Nike,P}+w_{ESPN,G}.w_{Male,P}+w_{Male,A}.w_{Nike,G} ϕ(w,x)=wESPN,A.wNike,P+wESPN,G.wMale,P+wMale,A.wNike,G,上式中 w E S P N , A w_{ESPN,A} wESPN,A学习(ESPN,NIKE)是因为Nike属于field广告,将上述公式化为: ϕ F F M ( w , x ) = ∑ j 1 = 1 n ∑ j 2 = j 1 + 1 n ( w j 1 , f 2 ⋅ w j 2 , f 1 ) x j 1 x j 2 {\phi _{FFM}}(w,x) = \sum\limits_{{j_1} = 1}^n {\sum\limits_{{j_2} = {j_1} + 1}^n {({w_{{j_1},{f_2}}} \cdot {w_{{j_2},{f_1}}})} } {x_{{j_1}}}{x_{j2}} ϕFFM(w,x)=j1=1∑nj2=j1+1∑n(wj1,f2⋅wj2,f1)xj1xj2其中 f 1 和 f 2 f_1和f_2 f1和f2是 j 1 和 j 2 所 属 的 f i e l d j_1和j_2所属的field j1和j2所属的field,那么FFM的参数为 n f k nfk nfk,通常 k F F M < < k F M k_{FFM}<<k_{FM} kFFM<<kFM,下表列举LM、Poly2、FM、FFM的参数和复杂度对比:

3.1、 Solving the Optimization Problem
使用AdaGrad算法来求解参数,具体过程如下所示:
1、随机采样一个点 ( y , x ) (y,x) (y,x)来更新参数,计算次梯度,并且只用计算非0值输入对应的参数,其梯度的计算如下所示:

2、对每个坐标 d = 1 , . . . , k d=1,...,k d=1,...,k,累计梯度的平方和: ( G j 1 , f 2 ) d ← ( G j 1 , f 2 ) d + ( g j 1 , f 2 ) d 2 ( 7 ) {{\rm{(}}{{\rm{G}}_{j1,f2}})_d} \leftarrow {{\rm{(}}{{\rm{G}}_{j1,f2}})_d} + {\rm{(}}{{\rm{g}}_{j1,f2}})_d^2 \qquad(7) (Gj1,f2)d←(Gj1,f2)d+(gj1,f2)d2(7) ( G j 2 , f 1 ) d ← ( G j 2 , f 1 ) d + ( g j 2 , f 1 ) d 2 ( 8 ) {{\rm{(}}{{\rm{G}}_{j2,f1}})_d} \leftarrow {{\rm{(}}{{\rm{G}}_{j2,f1}})_d} + {\rm{(}}{{\rm{g}}_{j2,f1}})_d^2 \qquad(8) (Gj2,f1)d←(Gj2,f1)d+(gj2,f1)d2(8)
3、最后, ( w j 1 , f 2 ) d 和 ( w j 2 , f 1 ) d (w_{j1,f2})_d和(w_{j2,f1})_d (wj1,f2)d和(wj2,f1)d由如下公式更新: ( w j 1 , f 2 ) d ← ( w j 1 , f 2 ) d − η ( G j 1 , f 2 ) d ( g j 1 , f 2 ) d ( 9 ) {({w_{j1,f2}})_d} \leftarrow {({w_{j1,f2}})_d} - {\eta \over {\sqrt {{{{\rm{(}}{{\rm{G}}_{j1,f2}})}_d}} }}{{\rm{(}}{{\rm{g}}_{j1,f2}})_d} \qquad(9) (wj1,f2)d←(wj1,f2)d−(Gj1,f2)dη(gj1,f2)d(9) ( w j 2 , f 1 ) d ← ( w j 2 , f 1 ) d − η ( G j 2 , f 1 ) d ( g j 2 , f 1 ) d ( 10 ) {({w_{j2,f1}})_d} \leftarrow {({w_{j2,f1}})_d} - {\eta \over {\sqrt {{{{\rm{(}}{{\rm{G}}_{j2,f1}})}_d}} }}{{\rm{(}}{{\rm{g}}_{j2,f1}})_d}\qquad(10) (wj2,f1)d←(wj2,f1)d−(Gj2,f1)dη(gj2,f1)d(10)其中 η \eta η是学习速率,由公式可以看出,学习速率可以自适应调整;具体的步骤如下所示:

3.3 Adding Field Information
对于FFM的输入格式,参考LibSVM输入格式, l a b l e f e a t : v a l 1 f e a t : v a l 2... lable \qquad feat:val1 \qquad feat:val2... lablefeat:val1feat:val2...,将FFM定义为: l a b l e f i e l d 1 : f e a t : v a l 1 f i e l d 2 : f e a t : v a l 2... lable \qquad field1:feat:val1 \qquad field2:feat:val2... lablefield1:feat:val1field2:feat:val2...,下面考虑几种典型的输入特征:
类别特征: 对于线性模型,一般将类别特征One-hot处理, 假设一个例子为
Y e s P : E S P N A : N i k e G : M a l e Yes \qquad P:ESPN \qquad A:Nike \qquad G:Male YesP:ESPNA:NikeG:Male
那么LibSVM的格式为:
Y e s P − E S P N : 1 A − N i k e : 1 G − M a l e : 1 Yes \qquad P-ESPN :1\qquad A-Nike :1 \qquad G-Male:1 YesP−ESPN:1A−Nike:1G−Male:1
对于One-hot来说,只有其中之一为1,其余为0,为了增加field的信息,可以考虑将一个类别作为一个field,那么其格式应为:
Y e s P : P − E S P N : 1 A : A − N i k e : 1 G : G − M a l e : 1 Yes \qquad P:P-ESPN :1\qquad A:A-Nike :1 \qquad G:G-Male:1 YesP:P−ESPN:1A:A−Nike:1G:G−Male:1
数值特征: 考虑下面的输入例子,也就是预测一篇文章是否能被会议接受:

一种比较简单的表示方法是将每个特征作为一个虚拟field,所以数据格式为:
Y e s A R : A R : 45.73 H i d x : H i d x : 2 C i t e : C i t e : 3 Yes \qquad AR:AR:45.73 \qquad Hidx:Hidx:2 \qquad Cite:Cite:3 YesAR:AR:45.73Hidx:Hidx:2Cite:Cite:3,但是这个存在问题:因为是数值型的,所以很少存在重复值;另一种方法就是先将连续值离散化,然后应用上面的类别特征表示方法,如:
Y e s A R : 45 : 1 H i d x : 2 : 1 C i t e : 3 : 1 Yes \qquad AR:45:1 \qquad Hidx:2:1 \qquad Cite:3:1 YesAR:45:1Hidx:2:1Cite:3:1,也就是将AR特征变为一个整数,但是这个也有问题:对于45.73,是45.7合适?45合适?40合适?甚至 i n t ( l o g ( 45.73 ) ) int(log(45.73)) int(log(45.73)),这种离散化方法丢掉了一些信息;
只有一个field的特征: 也就是所有特征属于一个field,这在NLP数据集中经常出现,如:

在上面这个例子中仅有field为sentence,如果我们将这个field分配所有的word,那么FFM就变为FM了;
4. EXPERIMENTS
作者发现FFM对于epoch的次数很敏感,所以使用了earlystoping方法;使用Kaggle比赛中的Criteo和Avazu数据集,如下所示:
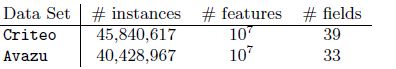
定义logloss公式为:
log l o s s = 1 m ∑ i = 1 m log ( 1 + exp ( − y i ϕ ( w , x i ) ) ) \log loss = {1 \over m}\sum\limits_{i = 1}^m {\log (1 + \exp ( - {y_i}\phi (w,{x_i})))} logloss=m1i=1∑mlog(1+exp(−yiϕ(w,xi)))其中m是测试集个数;
首先观察不同参数的影响, k k k(隐藏向量维度)、 λ 、 η \lambda、\eta λ、η,如下图所示(图中结果是针对测试集的):

图中表明K值影响不大, λ \lambda λ不能过大或者过小, η \eta η也是如此;
Early Stopping: 将数据集划分为测试集+验证集,在一个epoch后,计算验证集的Logloss,如果增大了,要么停止训练,要么用所得到的epoch数,重新用整个数据集训练一次;
但是存在一个问题:验证集误差最低,测试集不一定啊,作者考虑了其他方法来避免过拟合:如lazy update 和 ALS-based optimization methods,但结果表明没有使用验证集的EarlyStoping方法好;
最后给出一张不同模型的对比结果表:
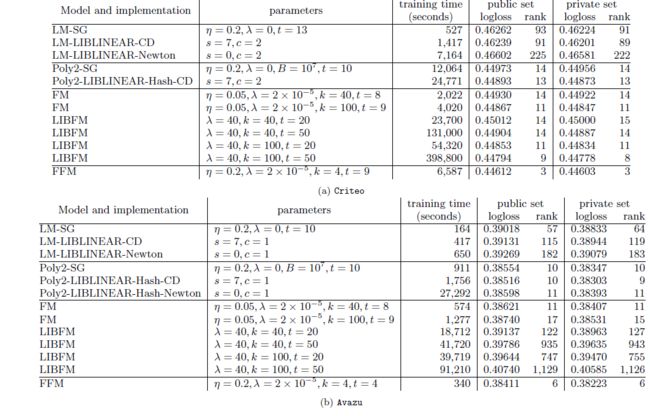
证明FFM效果还是可以的。