Recall, Precision, and Average Precision
原文出处:http://blog.csdn.net/pkueecser/article/details/8229166
在信息检索、分类体系中,有一系列的指标,搞清楚这些指标对于评价检索和分类性能非常重要,因此最近根据网友的博客做了一个汇总。
准确率、召回率、F1
信息检索、分类、识别、翻译等领域两个最基本指标是召回率(Recall Rate)和准确率(Precision Rate),召回率也叫查全率,准确率也叫查准率,概念公式:
召回率(Recall) = 系统检索到的相关文件 / 系统所有相关的文件总数
准确率(Precision) = 系统检索到的相关文件 / 系统所有检索到的文件总数
图示表示如下:
注意:准确率和召回率是互相影响的,理想情况下肯定是做到两者都高,但是一般情况下准确率高、召回率就低,召回率低、准确率高,当然如果两者都低,那是什么地方出问题了。一般情况,用不同的阀值,统计出一组不同阀值下的精确率和召回率,如下图:
如果是做搜索,那就是保证召回的情况下提升准确率;如果做疾病监测、反垃圾,则是保准确率的条件下,提升召回。
所以,在两者都要求高的情况下,可以用F1来衡量。
公式基本上就是这样,但是如何算图1中的A、B、C、D呢?这需要人工标注,人工标注数据需要较多时间且枯燥,如果仅仅是做实验可以用用现成的语料。当然,还有一个办法,找个一个比较成熟的算法作为基准,用该算法的结果作为样本来进行比照,这个方法也有点问题,如果有现成的很好的算法,就不用再研究了。
AP和mAP(mean Average Precision)
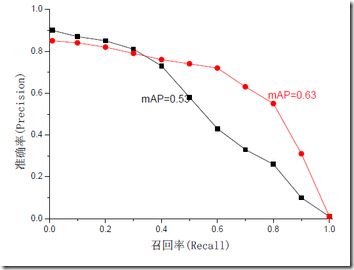
mAP是为解决P,R,F-measure的单点值局限性的。为了得到 一个能够反映全局性能的指标,可以看考察下图,其中两条曲线(方块点与圆点)分布对应了两个检索系统的准确率-召回率曲线
可以看出,虽然两个系统的性能曲线有所交叠但是以圆点标示的系统的性能在绝大多数情况下要远好于用方块标示的系统。
从中我们可以 发现一点,如果一个系统的性能较好,其曲线应当尽可能的向上突出。
更加具体的,曲线与坐标轴之间的面积应当越大。
最理想的系统, 其包含的面积应当是1,而所有系统的包含的面积都应当大于0。这就是用以评价信息检索系统的最常用性能指标,平均准确率mAP其规范的定义如下:(其中P,R分别为准确率与召回率)
ROC和AUC
ROC和AUC是评价分类器的指标,上面第一个图的ABCD仍然使用,只是需要稍微变换。
回到ROC上来,ROC的全名叫做Receiver Operating Characteristic。
ROC关注两个指标
True Positive Rate ( TPR ) = TP / [ TP + FN] ,TPR代表能将正例分对的概率
False Positive Rate( FPR ) = FP / [ FP + TN] ,FPR代表将负例错分为正例的概率
在ROC 空间中,每个点的横坐标是FPR,纵坐标是TPR,这也就描绘了分类器在TP(真正的正例)和FP(错误的正例)间的trade-off。ROC的主要分析工具是一个画在ROC空间的曲线——ROC curve。我们知道,对于二值分类问题,实例的值往往是连续值,我们通过设定一个阈值,将实例分类到正类或者负类(比如大于阈值划分为正类)。因此我们可以变化阈值,根据不同的阈值进行分类,根据分类结果计算得到ROC空间中相应的点,连接这些点就形成ROC curve。ROC curve经过(0,0)(1,1),实际上(0, 0)和(1, 1)连线形成的ROC curve实际上代表的是一个随机分类器。一般情况下,这个曲线都应该处于(0, 0)和(1, 1)连线的上方。如图所示。
用ROC curve来表示分类器的performance很直观好用。可是,人们总是希望能有一个数值来标志分类器的好坏。
于是Area Under roc Curve(AUC)就出现了。顾名思义,AUC的值就是处于ROC curve下方的那部分面积的大小。通常,AUC的值介于0.5到1.0之间,较大的AUC代表了较好的Performance。
mAP在图像detection中的应用
出自知乎
链接:https://www.zhihu.com/question/41540197/answer/91698989
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
在图像中,尤其是分类问题中应用AP,是一种评价ranking方式好不好的指标:
举例来说,我有一个两类分类问题,分别5个样本,如果这个分类器性能达到完美的话,ranking结果应该是+1,+1,+1,+1,+1,-1,-1,-1,-1,-1.
但是分类器预测的label,和实际的score肯定不会这么完美。按照从大到小来打分,我们可以计算两个指标:precision和recall。比如分类器认为打分由高到低选择了前四个,实际上这里面只有两个是正样本。此时的recall就是2(你能包住的正样本数)/5(总共的正样本数)=0.4,precision是2(你选对了的)/4(总共选的)=0.5.
图像分类中,这个打分score可以由SVM得到:s=w^Tx+b就是每一个样本的分数。
从上面的例子可以看出,其实precision,recall都是选多少个样本k的函数,很容易想到,如果我总共有1000个样本,那么我就可以像这样计算1000对P-R,并且把他们画出来,这就是PR曲线:
这里有一个趋势,recall越高,precision越低。这是很合理的,因为假如说我把1000个全拿进来,那肯定正样本都包住了,recall=1,但是此时precision就很小了,因为我全部认为他们是正样本。recall=1时的precision的数值,等于正样本所占的比例。
所以AP,average precision,就是这个曲线下的面积,这里average,等于是对recall取平均。而mean average precision的mean,是对所有类别取平均(每一个类当做一次二分类任务)。现在的图像分类论文基本都是用mAP作为标准。
上图中有一个AP11,这是把recall从0,0.1,0.2.一直到1.0的11个点的precision取平均得到的结果。VOC08之后AP11已经被抛弃了。
貌似从VOC08之后要求PR曲线必须单调下降了?这个不太确定。
================================================
1.使用AP会比accuracy要合理。对于accuracy,如果有9个负样本和一个正样本,那么即使分类器什么都不做全部判定为负样本accuracy也有90%。但是对于AP,recall=1那个点precision会掉到0.1.曲线下面积就会反映出来。
这里面详细地给出了概念的解释以及计算方式。