EM算法实例及python实现

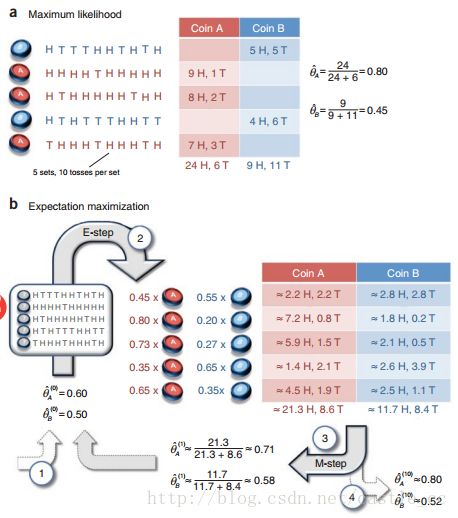
现在有两个硬币A和B，要估计的参数是它们各自翻正面（head）的概率。观察的过程是先随机选A或者B，然后扔10次。以上步骤重复5次。如果知道每次选的是A还是B，那可以直接估计（见下图a）。如果不知道选的是A还是B（隐变量），只观测到5次循环共50次投币的结果，这时就没法直接估计A和B的正面概率。EM算法此时可起作用（见下图b）。

稍微解释一下上图的计算过程。初始值θA=0.6,θB=0.5。
图中的0.45是怎么得来的呢？由两个硬币的初始值0.6和0.5，容易得出投掷出5正5反的概率是pA=C(10,5)(0.6^5)*(0.45)，pB=C(10,5)(0.5^5)*(0.55), pA/(pA+pB)=0.449, 0.45就是0.449近似而来的，表示第一组实验选择的硬币是A的概率为0.45。图中的2.2H，2.2T是怎么得来的呢？ 0.449 * 5H = 2.2H ，0.449 * 5T = 2.2T ，表示第一组实验选择A硬币且正面朝上次数的期望值是2.2。其他的值依次类推。

python代码实现：

import numpy as np
import math
input = np.array([[1, 0, 0, 0, 1, 1, 0, 1, 0, 1], 
                [1, 1, 1, 1, 0, 1, 1, 1, 1, 1],
                [1, 1, 0, 1, 1, 1, 1, 0, 1, 1],
                [1, 0, 1, 0, 0, 0, 1, 1, 0, 0],
                [0, 1, 1, 1, 0, 1, 1, 1, 0, 1]])
                
thetaA = 0.5
thetaB = 0.6
m, n = input.shape
headNums = input.sum(axis = 1)
tailNums = n - headNums

for i in range(10):
    pAHNum = 0
    pATNum = 0
    pBHNum = 0
    pBTNum = 0
    for headNum in headNums:
        pA = math.pow(thetaA, headNum) * math.pow((1 - thetaA), (n - headNum))
        pB = math.pow(thetaB, headNum) * math.pow((1 - thetaB), (n - headNum))
        pSum = pA + pB
        pA = pA / pSum
        pB = pB / pSum
        pAHNum += headNum * pA
        pATNum += (n - headNum)*pA
        pBHNum += headNum * pB
        pBTNum += (n - headNum)*pB

    thetaA = pAHNum / (pAHNum + pATNum)
    thetaB = pBHNum / (pBHNum + pBTNum)

算法实例原地址：What is the expectation maximization algorithm?