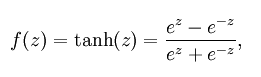数据分析---常见分类算法

分类问题是监督学习的一个核心问题。在监督学习中，当输出变量取有限个离散值时，预测问题便成为分类问题。

监督学习从数据中学习一个分类决策函数或分类模型，称为分类器（classifier）。分类器对新的输入进行输出的预测，这个过程称为分类。

 

KNN算法（k-NearestNeighbor）：

如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别。

所选择的邻居都是已经正确分类的对象。

对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

        现在有电器，水果，书籍3个种类的点，分布在第一象限（x表示价格，y表示销量），现在已知一个点m，我们需要找出离它最近的点（欧氏距离），根据这几个点的特征去分析，如果k=4，找4个点，其中3个 点属于水果类，那么，我们就断定这个点m也是水果。

KNN算法不仅可以用于分类，还可用于回归。通过找出一个样本的k个最近邻居，将这些邻居的属性的平均值赋给该样本，就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight)，如权值与距离成反比。

缺点：样本分布不均衡（有的类样本很少，有的超多），就会影响最后判断的结果。

 

朴素贝叶斯算法：

公式：                                  P(B|A) = P(A|B)*P(B) / P(A)

即：                                      P(类别|特征) = P(特征|类别)*P(类别) / P(特征)

           这个等式成立的条件需要特征之间相互独立,所以各属性之间相关性较小时，朴素贝叶斯性能比较好

即要满足这样：                   P(A)=P(A1*A2*A3...) = P(A1)*P(A2)*P(A3)...

上面的公式可以改成：       P(B|A) = P(A1|B)*P(A2|B)*P(A3|B)...  / P(A1)*P(A2)*P(A3)...

优点：分类过程中时空开销小（假设特征相互独立，只会涉及到二维存储）

 

决策树：

                        https://mp.csdn.net/postedit/85130080

 

人工神经网络：

目前，已有近40种神经网络模型，其中有反传网络、感知器、自组织映射、Hopfield网络、波耳兹曼机、适应谐振理论等

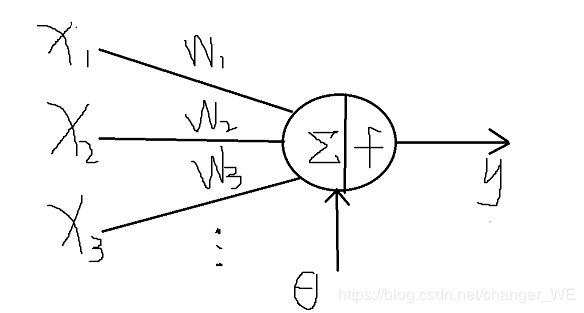
数学定义：

                     

来自其他处理单元（神经元）i的信息为Xi，每一条突触的权重（作用强度）是Wi，

                          左边：   

                           右边：                 

 θ（threshold）表示隐含层神经节点的阈值（大于这个值一种结果，小于这个值又一种结果，例如：买东西，价格小于10就买，大于10不买），f 称为激活函数

激活函数：

      由于上一层的输出是下一层的输入，导致上层到下层是一个线性过程，而线性模型的表达能力不够，所以引入非线性函数。

      常用的有：

              1）tanh（双切正切函数）：tanh在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果

                                                      

              2）sigmoid（s型函数）： 它可以将一个实数映射到(0,1)的区间，可以用来做二分类

                                                    

              3）ReLU （简单，大于0的留下，否则为0） 用于隐层神经元输出

 

从输入输出的结果中进行学习：

                            神经元权值和阈值的不断调整

学习规则：

 1） 误差修正型规则：属于有监督的学习方法，根据实际输出和期望输出的误差进行网络连接权值的修正，

                                         δ学习规则、Widrow-Hoff学习规则、感知器学习规则和误差反向传播的BP(Back Propagation)学习规则

  2）竞争型规则：属于无监督学习，没有期望输出，学习(训练)阶段与应用(工作)阶段成为一体

  3）Hebb型规则：利用神经元之间的活化值(激活值)来反映它们之间联接性的变化，根据活化值(激活值)来修正其权值

  4）随机型规则：根据目标函数（即网络输出均方差）的变化调整网络的参数，最终使网络目标函数达到收敛值

神经网络的运作：

                             

最困难的部分就是确定权重（w）和阈值（θ）。目前为止，这两个值都是自己主观给出的，但现实中很难估计它们的值，一般采用试错法，即微小的调整，得到效果最好的那一次调整。

支持向量机（Support Vector Machine, SVM）：

SVM是用来解决二分类问题的有监督学习算法

支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度，Accuracy）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折衷，以期获得最好的推广能力（或称泛化能力）。

泛化误差界的公式为：

                                     R(w)≤Remp(w)+Ф(n/h)

公式中R(w)就是真实风险，Remp(w)就是经验风险，Ф(n/h)就是置信风险。统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小，即结构风险最小。

SVM正是这样一种努力最小化结构风险的算法。

非线性，是指SVM擅长应付样本数据线性不可分的情况，主要通过松弛变量（也有人叫惩罚变量）和核函数技术来实现

维数高可以降维处理

线性分类器：

                                              

C1和C2是要区分的两个类别，中间的直线就是一个分类函数，如果存在一个线性函数能够将样本完全正确的分开，就称这些数据是线性可分的，否则称为非线性可分的。

线性函数：一维是一个点，二维是线，三维是面,高于三维称为超平面。一个线性函数是一个实值函数（即函数的值是连续的实数），通过分类函数执行时得到的值大于还是小于这个阈值来确定类别归属。

要将两类分开，就要找到一个超平面，使得超平面到两类的 margin 达到最大，margin就是超平面与离它最近一点的距离

算法方面：https://blog.csdn.net/liugan528/article/details/79448379