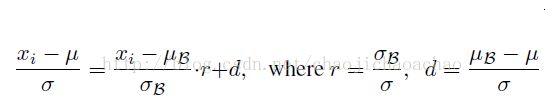论文心得:BatchNorm及其变体
本文记录BatchNormalization的总结思考及其拓展,目前收录BatchRenormalization、AdaBN、WeightNormalization、NormalizationPropagation。
0.BatchNormalization
该层的设计是为了解决Internal Covariate Shift的问题,这里首先要区分一下Internal Covariate Shift与Covariate Shift,前者是对层与层之间数值偏移的描述,
batchnorm对数值层面做了高斯均衡化,而后者是迁移学习中解决原空间和目标空间边缘分布不一致的一个分支问题,是对不同空间表征的偏移的描述。
batchnorm前传公式如下,反传由标准的链式法则给出(本文省略):因为输入变得很稳定,促进了模型的收敛并一定程度上阻止了过拟合,作者猜测BatchNormalization层的雅可比矩阵的奇异值接近1,这加速了模型的收敛速度。
从Bayesian的角度去解释batchnorm,首先引出PRML中解释的L2-NORM的由来:【似然函数*先验分布=后验分布,log(后验分布)=log(似然函数)+L2-NORM】,可知在log域的L2-NORM(即先验分布)对应原值域的高斯分布,因此目标函数的拟合相当于后验分布的拟合,对weight的L2-NORM 正则项是对weight先验分布的拟合,这种拟合压制了训练中weight的波动,而原值域的变化不仅依赖于weight,也依赖于输入X,因此batchnorm就是一种对X波动的压制,从这个意义上,batchnorm便可解释为对X的正则项。这种压制其实并不是刚刚出现的,所谓白化操作就是对输入数据的normalize,而batchnorm简化了其计算。
对后验分布的拟合使得模型去更快地适应数据,于是就加速了收敛。
实际用的时候再加入scale和shift,使得BN能够表达identity,这样卷积层inference时就不再依赖于miniBatch,如下式所示:
而scale与shift也对应着Bayesian解释,由于采用部分数据的分布作为所有数据的先验分布,其实便破坏了整个空间的原始表征,scale与shift就是在逆转对表征的破坏,逆转的程度由模型在训练中自己调整。通常将带scale和shift的BN层加在非线性激活函数之前,在caffe的官方版本中将bias转移到了batchnorm后面的scale层中。 BN的两个缺陷也很明显,因为是对mini-batch求统计信息,因此具有数据依赖性,数据的随机性会导致训练的不稳定,且batch=1时无法使用。而各种变体本质上就是在寻找Natural Gradient,在加速收敛的同时,保证模型的泛化能力。1.BatchRenormalization
这样一来,就相当于在训练阶段也使用moving averages μ和σ,这会引起梯度优化和normalization之间的冲突,优化的目的是通过对权重的scale和shift去适应一个minibatch,normalization则会抵消这种影响,而moving averages则消除了归一化后的激活对当前minibatch的依赖性,使得minibatch丧失了对每次权重更新方向的调整,从而使得权重尺度因normalization的抵消而无边界的增加却不会降低loss。而在前传中r和d的仿射变换修正了minibatch和普适样本的差异,使得该层的激活在inference阶段能得到更有泛化性的修正。
这样的修正使得minibatch很小甚至为1时的仍能发挥其作用,且即使在minibatch中的数据是非独立同分布的,也会因为这个修正而消除对训练集合的过拟合。
从Bayesian的角度看,这种修正比需要自己学习的scale和shift能更好地逆转对表征的破坏,且这种逆转的程度是由minibatch数据驱动的,在inference时也能因地制宜,而scale和shift对不同数据在inference时会施加相同的影响,因此这样的修正进一步降低了不同训练样本对训练过程的影响,也使得train和inference更为一致。
2.AdaBN
这个变体不是为了解决BN带来的缺陷,而是解决了一个BN没能很好解决的问题,就是当训练图像和测试图像不是同一个源时,需要不小的数据集进行finetune,AdaBN采用了一个简单粗暴的方法缓解了跨域的transfer learning,即domain adaption问题,公式如下:
其中j表示每一个神经元。 作者在实验中验证了该方法的有效性,adaption之后训练域和测试域的数据混杂地更为均衡,同时同一层的神经元之间的KL离散度降低,减小了域的差异。然而作者并没有给出详细的理论性的解释。
下表是KL离散度的对比:
作者将每个neuron的权值normalize为1,weight的优化便以另一种表达: 更新公式如下: 如此便解耦了权重向量的范数和方向,加速了收敛,保证了gradient的稳定,不会爆炸或者消失;同时解决了BN的数据依赖性,计算开销也降低了许多。 相比于BN,该方法没能将每一层特征尺度固定住,因此作者设计了一种初始化方法,在初始化时利用了mini-batch的信息,保证了features在初始化时为0均值,1方差。 作者在实验部分验证了该方法在CIFAR-10、Convolutional VAE、DRAW、DQN等模型中都取得了更好的结果;作者同时提出了两个extensions,一个是对参数g引入log-scale的参数s,即$g=e^(cs)$;一个是给v的范数设定一个范围,这样虽然延长了参数更新,但收敛后的测试性能会比较好。
4.NormalizationPropagation
该方法的论文详细论述了比WeightNormalization更多的理论意义和直观解释,主要思想就是对输入数据做normalization,然后将normalization的效果传递到后续的层中,下式是对该方法有效性的理论分析命题: 由上式可以看出:1)协方差矩阵近似是一个误差有界的对角矩阵,误差大小由W控制2)如果希望u有单位方差,则要除一个$||W_i||_2^2$,这实际上就是对WeightNormalization做出了解释。上式中的bound第一项在W归一化后为0了,第二项是与W的coherence(即列矩阵的相关系数)有关,而真实的数据确实比较低,这便又印证了1)。 下式以Relu为例,给出了数据进过非线性单元后的调整: 然后,作者严格地论述了NormalizationPropagation的雅可比矩阵的奇异值接近1(1.21)。最后给出了完整的全连接和卷积层的变换公式: 图1是试验中的各层mean对比,NormProp的各层mean达到稳定的速度更快且更接近0:
5.后言
综上,Normalization在深度网络中的价值是值得深度挖掘下去的。正如WeightNormalization文中提到的,从优化方面,基于一阶梯度的优化高度依赖于目标函数的曲率,如果目标在最优点的hessian矩阵的条件数太小,就是病态曲率,不同的参数化方法就会导致不同的曲率,通过Normalization来优化参数化的方法也不失为一个好的策略。
文献
1.Revisiting Batch Normalization For Practical Domain Adaptation
2.Weight Normalization: A Simple Reparameterizationto Accelerate Training of Deep Neural Networks
3.Normalization Propagation: A Parametric Technique for Removing Internal Covariate Shift in Deep Networks
4.Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
5.http://www.cnblogs.com/neopenx/p/5211969.html
6.Batch Renormalization: Towards Reducing Minibatch Dependence in Batch-NormalizedModels