Theano学习一:张量、计算图、操作算子等基础知识
文章目录
- 张量
- 1.1计算图和符号计算
- 1.2张量操作
- 1.2.1维度操作算子
- 1.2.2元素操作算子
- 1.2.3约减操作算子(张量变成标量)
- 1.2.4线性代数算子
张量
张量(tensor)是一个多维的数据存储形式,数据的的维度被称为张量的阶。它可以看成是向量和矩阵在多维空间中的推广,向量可以看成是一维张量,矩阵可以看成是两维的张量。在Python中,一些科学计算库(如Numpy)已提供了多维数组。Theano并不能取代Numpy,但可与之协同工作。Numpy可用于初始化张量。
为了在CPU和GPU上执行相同的计算,采用符号变量,并由张量类、抽象以及有变量节点和应用节点构建计算图的数字表达式表示。根据计算图的编译平台,张量可由下列任意一种形式替代:
- 1.TensorType变量,只用于CPU
- 2.GpuArrayType变量,只能用于GPU
这样,所编写的代码就与执行平台无关。
在此给出一些张量对象:
| 对象类 | 维度 | 示例 |
|---|---|---|
| Theano.tensor.scalar | 零维数组 | 2,3,5 |
| Theano.tensor.vector | 一维数组 | [0,3,20] |
| Theano.tensor.matrix | 二维数组 | [[2,3][1,5]] |
| Theano.tensor.tensor3 | 三维数组 | [[[2,3][1,5]],[[2,1][3,4]]] |
在Python shell中使用这些Theano对象具有更好的效果:
>>> import theano.tensor as T
>>> T.scalar()
<TensorType(float32, scalar)>
>>> T.iscalar()
<TensorType(int32, scalar)>
>>> T.fscalar()
<TensorType(float32, scalar)>
>>> T.dscalar()
<TensorType(float64, scalar)>
在对象之前的i,l,f或d表明给定张量类型为integer32、integer64、float32或float64。对于实值(浮点)数据,建议直接采用T.scalar()形式而不是f或d的形式,这是由于浮点数的配置可采用直接表示形式:
>>> import theano
>>> theano.config.floatX = 'float64'
>>> T.scalar()
<TensorType(float64, scalar)>
>>> T.fscalar()
<TensorType(float32, scalar)>
>>> theano.config.floatX='float32'
>>> T.scalar()
<TensorType(float32, scalar)>
符号变量的作用如下:
- 1.起到占位符的作用,作为构建数值运算(如加法、乘法)计算图的起点:一旦计算图编译完成,在评价过程中接收输入数据流。
- 2.表示中间结果或输出结果。
符号变量和操作都是计算图的一部分,在CPU或GPU上进行编译以实现快速执行。接下来,编写一个简单的计算图:
>>> x = T.matrix()
>>> y = T.matrix()
>>> z = x+y
>>> theano.pp(z)
'( + )'
>>> z.eval({x:[[1,2],[2,1]], y:[[2,6],[6,2]]})
array([[ 3., 8.],
[ 8., 3.]], dtype=float32)
首先,创建两个符号变量,或称为变量节点,记为x和y,并在两者之间通过一个加法操作,即应用节点在计算图中创建一个新的符号变量z。
输出函数pp可输出由Theano符号变量表示的表达式。Eval函数可在前两个变量x和y通过两个二维数值数组初始化后计算输出变量z的值。
下面的示例表明变量a和b之间的区别,分别记为aa和bb:
>>> a = T.matrix('aa')
>>> b = T.matrix('bb')
>>> theano.pp(a+b)
'(aa + bb)'
若没有命名,则在较大的计算图中跟踪节点会更加复杂。在输出计算图时,命名显然有助于诊断问题,而变量仅用于处理计算图中的对象:
>>> x = T.matrix('xx')
>>> x = x + x
>>> theano.pp(x)
'(xx + xx)'
再此,最初记为x的符号变量保持不变,仍作为计算图的一部分。x+x创建一个赋值给Python变量x的新符号变量。
另外,还需注意的是,在命名时,复数形式可同时初始化多个张量:
>>> x,y,z = T.matrices('xx','yy','zz')
>>> x
xx
>>> y
yy
>>> z
zz
接下来,讨论显示计算图的不同函数。
1.1计算图和符号计算
回顾上述的简单加法示例,并以不同形式来显示同样的信息:

其中,debugprint函数输出预编译计算图,即未优化的计算图。在本例中,该计算图由两个变量节点x和y,以及一个由no_inplace选项确定的按元素相加的应用节点组成。在优化计算图中采用inplace选项可节省内存并重用输入内存来保存计算结果。
如果已安装graphviz库(graphviz安装问题)和pydot库,则pydotprint命令可输出计算图的PNG图像:
![]()

或许大家已经注意到在第一次执行z.eval命令时花费一定时间。这种延迟的原因是需要在计算之前优化数学表达式并编译CPU和GPU的代码。
编译后的表达式可显示得到,并作为一个普通的Python函数来使用:

在函数创建中的第一个参数是表征计算图输入节点的变量列表。第二个参数是输出变量数组。通过下列命令可输出编译后的计算图:
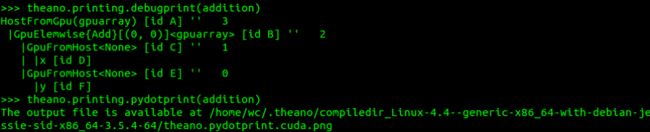
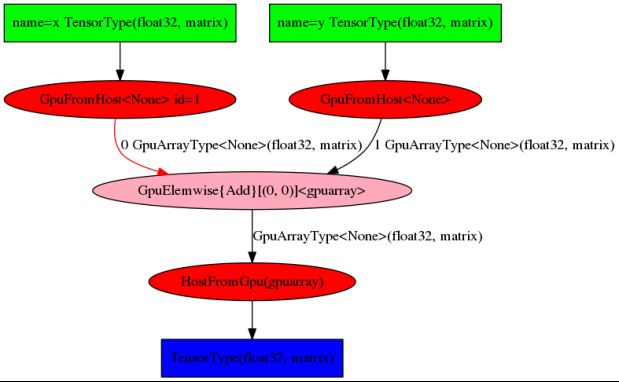
本例已表明在使用GPU时的输出情况。在编译过程中,每个操作都选择了GPU实现。主程序仍在数据所在的CPU上运行,GpuFromHost指令是将数据从CPU传输到GPU输入,而HostFromGpu正好相反,是获取主程序的结果并显示:
Theano可执行一些数学优化操作,如分组按元素操作,在上述加法运算上添加一个新值:

计算图中的节点个数并未增加:两种加法运算合并到一个节点中。这种优化会使得调试更加困难,因此会在本章最后介绍如何在调试时禁用优化。
最后,讨论如何利用NumPy来设置初始值:
在NumPy数组上执行函数会产生一个精度降低的相关错误,这是因为此处的NumPy数组是float64和int64 dtypes, 而x和y为float32。对此有多种解决方法:第一种解决方法是以正确dtype类型创建NumPy数组
![]()
另一种方法是转换NumPy数组类型(尤其是对于不允许直接选择dtype类型的numpy.diag):

或允许向下类型转换:

1.2张量操作
至此,已讨论了如何创建由符号变量和运算操作组成的计算图,并在GPU和CPU上编译赋值表达式或函数的结果。
由于张量对于深度学习非常重要,因此在Theano中提供了大量的张量运算算子。在科学计算库(如用于数值数组的NumPy库)中存在的大多数算子在Theano中等价并具有类似的命名,以便于NumPy用户更加熟悉。但与NumPy不同的是,在Theano中创建的表达式可在CPU或GPU上编译。
例如:下面是张量创建的情况:
T.zeros()、T.ones()、T.eye()算子一个形状元组作为输入;
T.zeros_like()、T.one_like()、T.identity_like()算子采用张量参数的形状;
T.arange()、T.mgrid()、T.ogrid()算子用于排列和网格阵列。
下面给出如何在Python shell应用:
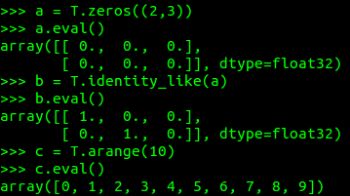
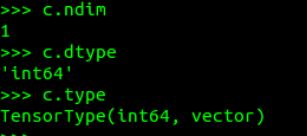
如位数(ndim)和类型(dtype)等信息在创建张量时定义,且不能修改:
而形状等其他一些信息通过计算图来计算:
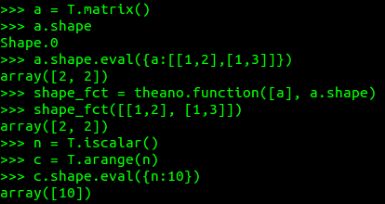
1.2.1维度操作算子
第一类张量算子是维度操作算子。这种算子是以张量作为输入,并返回一个新的张量:
| 算子 | 描述 |
|---|---|
| T.reshape() | 重构张量维数 |
| T.fill() | 用相同值填充数组 |
| T.flatten() | 返回一个一维张亮的所有元素(向量) |
| T.dimshuffle() | 改变维度顺序,有点类似NumPy中的转置方法,主要区别时刻用于增加或去除broadcastable维度(长度为1) |
| T.squeeze() | 通过去除等于1的维度来重构 |
| T.transpose() | 转置 |
| T.swapaxes() | 交换维度 |
| T.sort、T.argsort() | 排序张量或按顺序索引 |
例如:重构算子的输出是一个新的张量,其中包含顺序相同但形状不同的相同元素:
该算子可构成链的形式:
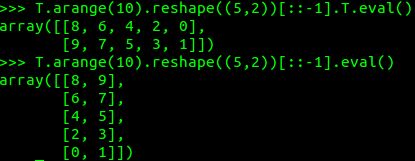
PS:在Python中通过索引访问普通[::-1]数组的方法和T.transpose中.T的用法。
1.2.2元素操作算子
在多维数组上的第二类算子是元素操作算子。
第一类的按元素操作是以两个相同维度的输入张量,并按元素执行应用函数f,这意味着所有元素对各自张量具有相同坐标f([a,b],[c,d])=[f(a,c),f(b,d)],比如[a,b]+[c,d]=[a+c,b+d]。例如下面的乘法运算:
>>> import theano
Can not use cuDNN on context None: Use cuDNN 7.0.2 or higher for Volta.
Mapped name None to device cuda: GeForce RTX 2070 (0000:01:00.0)
>>> import theano.tensor as T
>>> a,b = T.matrices('a','b')
>>> z=a*b
>>> import numpy
>>> z.eval({a:numpy.ones((2,2)).astype(theano.config.floatX), b:numpy.diag((3,3)).astype(theano.config.floatX)})
array([[ 3., 0.],
[ 0., 3.]], dtype=float32)
同样的乘法运算还可以写成以下形式:
>>> z=T.mul(a,b)
T.add和T.mul算子可接受任意个数的输入:
>>> z=T.mul(a,b,a,b)
而一些元素操作算子只能接受一个输入张量f([a,b])=[f(a),f(b)]:
>>> a=T.matrix()
>>> z=a**2
>>> z.eval({a:numpy.diag((3,3)).astype(theano.config.floatX)})
array([[ 9., 0.],
[ 0., 9.]], dtype=float32)
最后,介绍一个广播机制。当输入张量不具有相同个数的维度时,就会广播所缺失的维度,这意味着该张量将沿着这一维度不断重复,以匹配另一个张量的维度。例如,取一个多维张量和一个标量(零维)张量,标量将在与多维张量相同形状的数组中不断重复,以使得最终形状匹配,并可按元素执行操作,f([a,b],c)=[f(a,c),f(b,c)]:
>>> a = T.matrix()
>>> b = T.scalar()
>>> z=a*b
>>> z.eval({a:numpy.diag((3,3)).astype(theano.config.floatX),b:3})
array([[ 9., 0.],
[ 0., 9.]], dtype=float32)
看另一示例:
>>> import theano
>>> import numpy
>>> import theano.tensor as T
>>> r = T.row()
>>> r.broadcastable
(True, False)
>>> mtr = T.matrix()
>>> mtr.broadcastable
(False, False)
>>> f_row = theano.function([r, mtr], r + mtr)
>>> R = numpy.arange(3).reshape(1,3).astype(theano.config.floatX)
>>> print(R)
[[ 0. 1. 2.]]
>>> M = numpy.arange(9).reshape(3, 3).astype(theano.config.floatX)
>>> print(M)
[[ 0. 1. 2.]
[ 3. 4. 5.]
[ 6. 7. 8.]]
>>> print(f_row(R, M))
[[ 0. 2. 4.]
[ 3. 5. 7.]
[ 6. 8. 10.]]
>>> print()
>>> c = T.col()
>>> c.broadcastable
(False, True)
>>> f_col = theano.function([c, mtr], c + mtr)
>>> C = numpy.arange(3).reshape(3, 1).astype(theano.config.floatX)
>>> print(C)
[[ 0.]
[ 1.]
[ 2.]]
>>> M = numpy.arange(9).reshape(3, 3).astype(theano.config.floatX)
>>> print(M)
[[ 0. 1. 2.]
[ 3. 4. 5.]
[ 6. 7. 8.]]
>>> print(f_col(C, M))
[[ 0. 1. 2.]
[ 4. 5. 6.]
[ 8. 9. 10.]]
下面是按元素操作算子示例:
| 算子 | 其他形式 | 描述 |
|---|---|---|
| T.add、T.sub、T.mul、T.truediv | +、-、*、/ | 加、减、乘、除 |
| T.pow、T.sqrt | 幂、平方根 | |
| T.exp、T.log | 指数、对数 | |
| T.cos、T.sin、T.tan | 余弦、正弦、正切 | |
| T.cosh、T.sinh、T.tanh | 双曲三角函数 | |
| T.intdiv、T.mod | //、% | 整除、模 |
| T.floor、T.ceil、T.round | 取整算子 | |
| T.sgn | 符号 | |
| T.and_、T.xor、T.or_、T.invert | &、^、 | 、~ |
| T.gt、T.lt、T.ge、T.le | >、<、>=、<= | 比较云算法 |
| T.eq、T.neq、T.isclose | 等于、不等于、公差接近 | |
| T.isnan | 是否为无穷大(不是数字) | |
| T.abs_ | 绝对值 | |
| T.minimum、T.maximum | 元素最大值和最小值 | |
| T.clip、T.swith | 最大值和最小值之间的值、转换 | |
| T.cast | 张量类型转换 |
按元素操作算子总是返回与输入数组相同大小的数组。T.switch和T.clip可接受3个输入。
特别是,T.switch将按元素执行传统的switch运算:
>>> cond = T.vector('cond')
>>> x,y = T.vectors('x', 'y')
>>> z = T.switch(cond, x, y)
>>> z.eval({cond:[1,0], x:[10,10], y:[3,2]})
array([ 10., 2.], dtype=float32)
在cond张量为真的同一位置,返回x值;反之,若cond为假,则返回y值。
对于T.switch算子,具有一个以标量而非张量的特定等价(ifelse)。这并不是一种按元素的运算,支持延迟求值(如果在计算结束之前已知答案,则无需计算所有的元素):
>>> from theano.ifelse import ifelse
>>> z = ifelse(1,5,4)#类似于一个三目运算符,第一个数非零表达式为第一个数,反之为第二个数
>>> z.eval()
array(5, dtype=int8)
1.2.3约减操作算子(张量变成标量)
另一种张量操作是约减,在大多数情况下是将所有元素约减为一个标量,为此,需要扫描张量的所有元素来计算输出:
| 算子 | 描述 |
|---|---|
| T.max、T.argmax、T.max_and_argmax | 最大值、最大值序号 |
| T.min、T.argmin | 最小值、最小值序号 |
| T.sum、T.prod | 元素之和或元素之积 |
| T.mean、T.var、T.std | 均值、方差和标准差 |
| T.all、T.any | 所有元素的与运算和或运算 |
| T.ptp | 元素排列(最小、最大) |
上述运算也可通过指定一个轴按行或按列操作,并沿着维度减小的方向执行:
>>> a = T.matrix('a')
>>> T.max(a).eval({a:[[1,2],[3,4]]})
array(4.0, dtype=float32)
>>> T.max(a,axis=0).eval({a:[[1,2],[3,4]]})
array([ 3., 4.], dtype=float32)
>>> T.max(a,axis=1).eval({a:[[1,2],[3,4]]})
array([ 2., 4.], dtype=float32)
model =np.array([[6,9,7,8]])
modell =np.array([[6],[9],[7],[8]])
#T.argmax()中的axis在等于0时,按列比较,取得最大值的下标索引;等于1时,按行比较。默认不写时,智能返回最大行,列下标索引
model =np.array([[6,9,7,8]])
modell =np.array([[6],[9],[7],[8]])
y_pred = T.argmax(model, axis=1)
y_predd = T.argmax(model)
y_pred2 = T.argmax(model,axis=0)
print(y_pred.eval())
print(y_predd.eval())
print(y_pred2.eval())
print("=======================")
y_pred = T.argmax(modell, axis=1)
y_predd = T.argmax(modell)
y_pred2 = T.argmax(modell,axis=0)
print(y_pred.eval())
print(y_predd.eval())
print(y_pred2.eval())
1.2.4线性代数算子
第三类操作运算算子是线性代数算子,如矩阵乘法:
A ∙ B = [ c i , j ] = [ ∑ k a i , k b k , j ] A \bullet B=[c_i,_j]=[\sum_{k}a_i,_kb_k,_j] A∙B=[ci,j]=[k∑ai,kbk,j]
也称为向量内积:
V ∙ W = ∑ k v k w k V \bullet W=\sum_{k}v_kw_k V∙W=k∑vkwk
| 算子 | 描述 |
|---|---|
| T.dot | 矩阵乘法/内积 |
| T.outer | 外积 |
另外,还有一些广义操作(指定轴的T.tensordot)或批量操作(batched_dot、batched_tensordot)。
最后,还存在一些非常有用的操作算子,但不属于前面的任何一类:T.concatenate是沿指定维度扩展张量,T.stack是在输入张量中创建一个新的维度,T.stacklist是创建一种张量叠加的新模式:
>>> a = T.arange(10).reshape((5,2))
>>> b = a[::-1]
>>> b.eval()
array([[8, 9],
[6, 7],
[4, 5],
[2, 3],
[0, 1]])
>>> a.eval()
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
>>> T.concatenate([a,b]).eval()
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9],
[8, 9],
[6, 7],
[4, 5],
[2, 3],
[0, 1]])
>>> T.concatenate([a,b],axis=1).eval()
array([[0, 1, 8, 9],
[2, 3, 6, 7],
[4, 5, 4, 5],
[6, 7, 2, 3],
[8, 9, 0, 1]])
>>> T.stack([a,b]).eval()
array([[[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]],
[[8, 9],
[6, 7],
[4, 5],
[2, 3],
[0, 1]]])
Numpy表达式等效的a[5:]=5和a[5:]+=5是以两种函数存在:
>>> a.eval()
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
>>> T.set_subtensor(a[3:], [-1,-1]).eval()
array([[ 0, 1],
[ 2, 3],
[ 4, 5],
[-1, -1],
[-1, -1]])
>>> T.inc_subtensor(a[3:],[-1,-1]).eval()
array([[0, 1],
[2, 3],
[4, 5],
[5, 6],
[7, 8]])
与NumPy的语法不同,不会改变原始张量,而是创建一个表示结果改变的新变量。因此,原始变量a仍为原值,而返回的变量(在此未定义)表示更新后的值,用户可以在随后的计算中使用该新变量。