TensorFlow演示反卷积的操作
一 反卷积函数介绍
1 语法格式
def conv2d_transpose(value,filter,output_shape,strides,padding="SAME",data_format="NHWC",name=None):
2 参数说明
value:代表通过卷积操作之后的张量,一般为NHWC类型。
filter:代表卷积核。
output_shape:代表输出的张量形状也是个四维张量。
strides:代表步长。
padding:代表原数据生成value时使用的补0的方式,是用来检查输入形状和输出形状是否合规的。
3 返回值
反卷积后的结果,按照output_shape指定的形状。
注意:NHWC类型是神经网络中处理图像方面常用的类型,4个字母分别代表4个意思,即N——个数、H——高、W——宽、C——通道数。也就是我们常见的四维张量。
二 实战
1 实例描述
通过对模拟数据进行卷积操作和反卷积操作,来比较卷积与反卷积中padding在SAME、VALID下的变化。
2 代码
import tensorflow as tf
'''
模拟数据
'''
img = tf.Variable(tf.constant(1.0,shape = [1, 4, 4, 1]))
filter = tf.Variable(tf.constant([1.0,0,-1,-2],shape = [2, 2, 1, 1]))
'''
分别进行VALID与SAME操作
'''
conv = tf.nn.conv2d(img, filter, strides=[1, 2, 2, 1], padding='VALID')
cons = tf.nn.conv2d(img, filter, strides=[1, 2, 2, 1], padding='SAME')
print(conv.shape)
print(cons.shape)
'''
再进行反卷积
'''
contv= tf.nn.conv2d_transpose(conv, filter, [1,4,4,1],strides=[1, 2, 2, 1], padding='VALID')
conts = tf.nn.conv2d_transpose(cons, filter, [1,4,4,1],strides=[1, 2, 2, 1], padding='SAME')
with tf.Session() as sess:
sess.run(tf.global_variables_initializer() )
print("conv:\n",sess.run([conv,filter]))
print("cons:\n",sess.run([cons]))
print("contv:\n",sess.run([contv]))
print("conts:\n",sess.run([conts]))
3 运行结果
(1, 2, 2, 1)
(1, 2, 2, 1)
conv:
[array([[[[-2.],
[-2.]],
[[-2.],
[-2.]]]], dtype=float32), array([[[[ 1.]],
[[ 0.]]],
[[[-1.]],
[[-2.]]]], dtype=float32)]
cons:
[array([[[[-2.],
[-2.]],
[[-2.],
[-2.]]]], dtype=float32)]
contv:
[array([[[[-2.],
[ 0.],
[-2.],
[ 0.]],
[[ 2.],
[ 4.],
[ 2.],
[ 4.]],
[[-2.],
[ 0.],
[-2.],
[ 0.]],
[[ 2.],
[ 4.],
[ 2.],
[ 4.]]]], dtype=float32)]
conts:
[array([[[[-2.],
[ 0.],
[-2.],
[ 0.]],
[[ 2.],
[ 4.],
[ 2.],
[ 4.]],
[[-2.],
[ 0.],
[-2.],
[ 0.]],
[[ 2.],
[ 4.],
[ 2.],
[ 4.]]]], dtype=float32)]
4 运行说明
为了便于观察,先整理一下结果
conv:
[array([[[[-2.],
[-2.]],
[[-2.],
[-2.]]]], dtype=float32),
array([[[[ 1.]],
[[ 0.]]],
[[[-1.]],
[[-2.]]]], dtype=float32)]
cons:
[array([[[[-2.],
[-2.]],
[[-2.],
[-2.]]]], dtype=float32)]
contv:
[array([[[[-2.],
[ 0.],
[-2.],
[ 0.]],
[[ 2.],
[ 4.],
[ 2.],
[ 4.]],
[[-2.],
[ 0.],
[-2.],
[ 0.]],
[[ 2.],
[ 4.],
[ 2.],
[ 4.]]]], dtype=float32)]
conts:
[array([[[[-2.],
[ 0.],
[-2.],
[ 0.]],
[[ 2.],
[ 4.],
[ 2.],
[ 4.]],
[[-2.],
[ 0.],
[-2.],
[ 0.]],
[[ 2.],
[ 4.],
[ 2.],
[ 4.]]]], dtype=float32)]
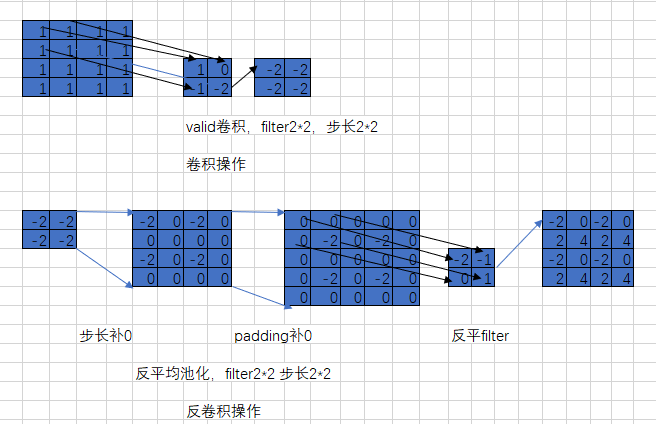
先定义一个[1,4,4,1]的矩阵,矩阵里的值全为1,进行filter为2*2、步长为2*2的卷积操作,分别使用padding为SAME和VALID的两种情况生成卷积数据,然后将结果放到conv2d_transpose里,再次使用padding为SAME和VALID的两种情况生成数据。
可以看出输出的结果与上图是一样的,并且也验证了当padding为SAME并且不需要补0时,卷积和反卷积对于padding是SAME和VALID都是相同的。