计算机科学家的核心
△向上生长, TO BE TO UP. 程序员成长充电站△
计算机基础课第 31 期分享
转载请联系授权(微信ID:qianpangzi0206)
作为未来的计算机科学家你可能会问:有没有更高效的排序算法?
01
归并排序
回到未排序的数组,试另一个算法 "归并排序"。第一件事是检查数组大小是否 > 1,如果是,就把数组分成两半,因为数组大小是 8,所以分成两个数组,大小是 4,但依然大于 1,所以再分成大小是 2 的数组,最后变成 8 个数组,每个大小为 1,现在可以"归并"了,"归并排序"因此得名。
从前两个数组开始,读第一个(也是唯一一个)值307 和 239,239 更小,所以放前面,剩下的唯一数字是 307 ,所以放第二位,成功合并了两个数组。重复这个过程,按序排列,然后再归并一次。同样,取前两个数组,比较第一个数239 和 214,214 更小,放前面。再看两个数组里的第一个数:239 和 250,239 更小,所以放下一位。看剩下两个数:307 和 250,250 更小,所以放下一位,最后剩下 307 ,所以放最后。
每次都以 2 个数组开始,然后合并成更大的有序数组,我们把刚隐藏起来的,下面的数组也这样做。现在有两个大小是 4 的有序数组,就像之前,比较两个数组的第一个数,取最小数,就像之前,比较两个数组的第一个数,取最小数,重复这个过程,直到完成,就排好了。
但坏消息是:无论排多少次,你还是得付 214 美元到印第安纳波利斯,总之,"归并排序"的算法复杂度是 O(n * log2 n)。n 是需要 比较+合并 的次数和数组大小成正比,log N 是合并步骤的次数。
例子中把大小是 8 的数组,分成四个数组,然后分成 2 个,最后分成 1 个,分了 3 次,重复切成两半,和数量成对数关系Log2 8=3。如果数组大小变成 16 - 之前的两倍,也只要多分割 1 次。因为 log2 16=4,即使扩大一千倍,从8到8000,分割次数也不会增大多少。Log2 8000≈13,13 比 3 只是4倍多一点。然而排序的元素多得多,因此"归并排序"比"选择排序"更有效率。
02
图搜索
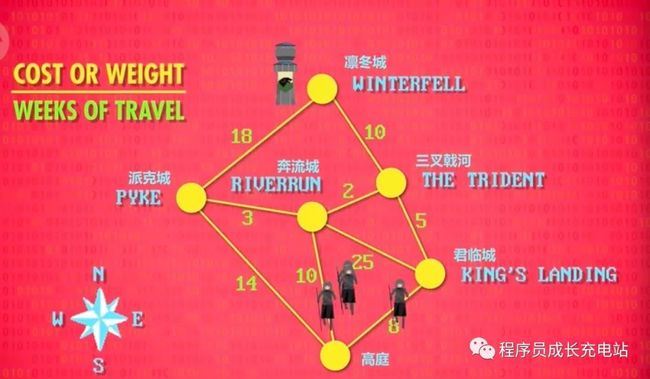
有好几十种排序算法,但没时间讲,所以我们来谈一个经典算法问题:图搜索。"图" 是用线连起来的一堆 "节点",可以想成地图,每个节点是一个城市,线是公路。一个城市到另一个城市,花的时间不同,可以用 成本(cost) 或 权重(weight) 来代称。
假设想找"高庭"到"凛冬城"的最快路线,最简单的方法是尝试每一条路,计算总成本,这是蛮力方法。假设用蛮力方法 来排序数组,尝试每一种组合,看是否排好序,这样的时间复杂度是 O(n!)。n 是节点数,n! 是 n 乘 n-1 乘 n-2... 一直到 1,比 O(n*n ) 还糟糕。
03
Dijkstra 算法
我们可以更聪明些,图搜索问题的经典算法,发明者是理论计算机科学的伟人 Edsger Dijkstra,所以叫 "Dijkstra 算法"。从"北京"开始,此时成本为0,把0标在节点里,其他城市标成问号,因为不知道成本多少。Dijkstra 算法总是从成本最低的节点开始,目前只知道一个节点 "高庭", 所以从这里开始,跑到所有相邻节点,记录成本,完成了一轮算法。但还没到"凛冬城",所以再跑一次 Dijkstra 算法,"高庭" 已经知道了,下一个成本最低的节点,是 "君临城"。就像之前,记录所有相邻节点的成本,到"三叉戟河"的成本是 5,然而我们想记录的是,从"高庭"到这里的成本,所以"三叉戟河"的总成本是 8+5=13周,现在走另一条路到"奔流城",成本高达 25 ,总成本 33。但 "奔流城" 中最低成本是 10,所以无视新数字,保留之前的成本 10,现在看了"君临城"的每一条路,还没到"凛冬城" 所以继续。
下一个成本最低的节点,是"奔流城",要 10 周,先看 "三叉戟河" 成本: 10+2=12,比之前的 13 好一点,所以更新 "三叉戟河" 为 12,"奔流城"到"派克城"成本是 3,10+3=13,之前是14,所以更新 "派克城" 为 13。"奔流城"出发的所有路径都走遍了, 你猜对了,再跑一次 Dijkstra 算法,下一个成本最低的节点,是"三叉戟河"。从"三叉戟河"出发,唯一没看过的路,通往"凛冬城"!成本是 10,加"三叉戟河"的成本 12,总成本 22。
再看最后一条路,"派克城"到"凛冬城",成本 31现在知道了最低成本路线,让军队最快到达,,还绕过了"君临城"。
Dijkstra 算法的原始版本,构思于 1956 年,算法复杂度是 O(n*n),前面说过这个效率不够好,意味着输入不能很大,比如美国的完整路线图。幸运的是,Dijkstra 算法几年后得到改进,变成 O(n log n + l),n 是节点数,l 是多少条线。虽然看起来更复杂,但实际更快一些。
用之前的例子,可以证明更快(6 个节点 9 条线),从 36 减少到 14 左右。
04
计算机科学家的核心
就像排序,图搜索算法也有很多,有不同优缺点,每次用谷歌地图时,类似 Dijkstra 的算法就在服务器上运行,找最佳路线。算法无处不在,现代世界离不开它们,这节只触及了算法的冰山一角。但成为计算机科学家的核心是根据情况合理决定用现有算法还是自己写新算法,希望这节的小例子能让你体会到这点。
下节我们开始讲数据结构。
相关阅读:
函数的强大之处
算法入门
程序员成长充电站
长按扫码关注,每天五分钟学习计算机最基础的知识和原理