ACO蚁群算法

蚁群算法也是比较经典的优化算法，这篇文章主要参考了作者 包子阳、余继周的《智能优化算法及其matlab实例》中的第5章内容，主要是使用aco算法寻找目标函数fun(x,y)的最小值。

%==========函数1：蚁群算法

function [minValue,minX,minY]=aco(m,G,Rho,P0,Xmax,Xmin,Ymax,Ymin)

X=zeros(m,2);%记录每个蚂蚁的位置
Tau=zeros(1,m);%每个蚂蚁在当前位置的目标函数值
trace=zeros(1,G);%每次寻优过程得到的最小目标函数值
for i=1:1:m
    X(i,1)=(Xmin+(Xmax-Xmin)*rand);
    X(i,2)=(Ymin+(Ymax-Ymin)*rand);
    Tau(i)=fun(X(i,1),X(i,2));
end

step=0.1;%局部搜索步长
P=zeros(G,m);%存放每个蚂蚁在每次循环中的状态转移概率
for NC=1:1:G
    lamda=1/NC;
    [Tau_best,BestIndex]=min(Tau);%寻找使目标函数最小值
    %计算状态转移概率
    for i=1:1:m
        P(NC,i)=(Tau(BestIndex)-Tau(i))/Tau(BestIndex);
    end
    % % % 更新每个蚂蚁的位置
    for i=1:1:m
        %局部搜索
        if P(NC,i)             t1=X(i,1)+(2*rand-1)*step*lamda;
            t2=X(i,2)+(2*rand-1)*step*lamda;
        else
            t1=X(i,1)+(Xmax-Xmin)*(rand-0.5);
            t2=X(i,2)+(Ymax-Ymin)*(rand-0.5);
        end
        %边界处理
        if t1             t1=Xmin;
        end
        if t1>Xmax
            t1=Xmax;
        end
        if t2             t2=Ymin;
        end
        if t2>Ymax
            t2=Ymax;
        end
        %判断蚂蚁是否移动
        if fun(t1,t2)             X(i,1)=t1;
            X(i,2)=t2;
        end
    end
    % % % 更新每个蚂蚁的信息素
    for i=1:1:m
        Tau(i)=(1-Rho)*Tau(i)+fun(X(i,1),X(i,2));
    end
    [value,index]=min(Tau);
    trace(NC)=fun(X(index,1),X(index,2));
end

[min_value,min_index]=min(Tau);
minX=X(min_index,1);minY=X(min_index,2);
minValue=fun(X(min_index,1),X(min_index,2));
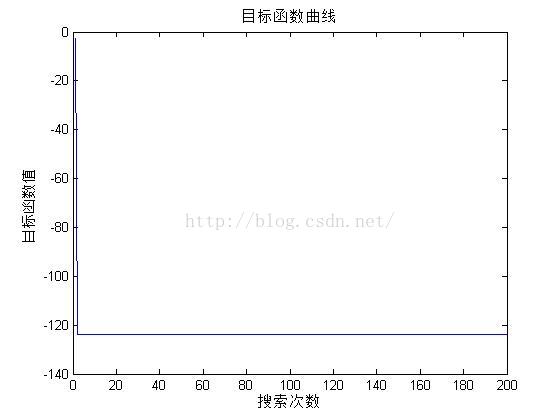
figure(1);clf
plot(trace);
xlabel('搜索次数');ylabel('目标函数值');
title('目标函数曲线');
figure(2);clf
x=Xmin:0.05:Xmax;
y=Ymin:0.05:Ymax;
z=zeros(length(x));
for i=1:1:length(x)
    for j=1:1:length(y)
        z(i,j)=fun(x(i),y(j));
    end
end
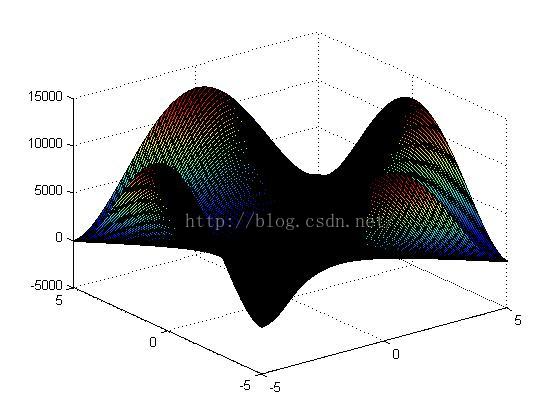
surf(x,y,z);

%============函数2：目标函数

function out=fun(x,y)
out=20*power((power(x,2)-power(y,2)),2)-power(1-y,2)-3*power(1+y,2)+0.3;

%===========函数演示与结果

[Z,X,Y]=aco(20,200,0.9,0.2,5,-5,5,-5);

结果：

使目标函数取最小值 Z=-123.7000，此时X=5,Y=5

结果如下图，因为目标函数对X Y有对称性，实际的最小值点有4个：(-5,-5)/(-5,5)/(5,-5)/(5,5)