Semi-Supervised Learning

简介

半监督学习主要是研究如何在有标签和无标签的数据中学习，其目的是设计算法来满足既包含有标记数据，又包含无标记数据的情况，并理解对于这种混合数据下学习的差异性。很多时候，人工标记的数据是很少的，而且代价是很大的，为了改善在缺少训练数据情况下的有监督学习，可以使用半监督学习来利用未标记数据。这里，主要介绍几种半监督学习的算法，如self-training、mixture models、co-training、graph-based methods和semi-supervised support vector machines。半监督学习的成功是基于一些关键性假设的，所以具有一定的适用性。对半监督学习的研究主要有两个方面的原因：实际价值体现在构建更好的算法；理论价值体现在可以更好地理解机器和人的学习方式。

非监督学习任务主要包括以下三种：

• 聚类
• 异常点检测
• 降维

监督学习：

• 分类
• 回归

从字面意思看，半监督学习是介于有监督学习和无监督学习中间的一种机器学习方法。事实上，半监督学习是有监督学习或无监督学习的一种延伸，只是其中包含了一些附加信息。主要包括：

• Semi-supervised classification
  这是有监督分类的延伸，训练数据包含 l 个有标签的样本和 u 个无标签样本，通常情况下 l≫u 。半监督分类的目标是从有标签和无标签数据中训练一个分类器，使得分类器的性能优于只用有标签数据训练得到的分类器。
• Constrained clustering
  这是无监督聚类的延伸，训练数据包含无标签样本和一些有监督的信息，如must-link约束，某些样本必须在同一个类别中；cannot-link约束，某些样本不能在同一个类别中；某些类别中样本数的限制。Constrained clustering的目标是获得一个相比于用无标签数据聚类更好的聚类。

除了上面两种无监督学习的方法，如基于有标签和无标签数据的回归、基于有标签数据的降维等。这里主要介绍半监督分类。

乍一看，似乎存在一个矛盾，即从无标签数据中学习预测器 f ，但 f 是从样本到标签的映射，而无标签数据不提供任何映射的样本。可以这么做是因为针对未标记数据的分布 P(x) 和目标标签之间的联系做了某些假设(link assumptions)。下面通过一个例子来说明。

下图是一个简单的半监督学习的例子。每个样本只有一个特征，总共存在两个类别：正例和负例。

考虑以下两种场景：

• 在有监督学习中，给定两个有标签的样本 (x1,y1)=(−1,−) 和 (x2,y2)=(1,+) ，显然，决策边界的最佳估计是 x=0 ：所有 x<0 的样本被划分为负类， x>0 的样本被划分为正类。
• 另外，给定了大量的无标记样本，即图中的绿色点。通过观察发现，他们形成了两个group。假设每个类别中的样本构成一个高斯分布，类中的样本围绕一个中心平均值。虽然没有标签，但是这部分无标记的样本可以给我们提供额外的信息。从图中可以看出，两个有标签数据并能很好地代表两个类，决策边界的半监督估计将在这两个group中间，即 x≈0.4 。

如果假设是正确的，则使用有标签和无标签数据可以得到一个更可靠的决策边界的估计。也就是说，无标签数据的分布可以帮助确定具有相同标签的数据所在的区域，然后通过少量的有标签数据来确定真实的label。

说明：对于一个特定的任务，盲目地选择一个半监督学习方法并不一定能在监督学习的基础上进一步改善性能。实际上，错误的假设会导致比监督学习更糟糕的结果。目前，主要的观点是半监督学习的表现取决于模型所提出的假设的正确性。

例：考虑一个二分类问题，每个类都服从高斯分布，两个高斯分布有部分重叠，如下图所示。真正的决策边界在两个分布的中间，如图中虚线所示。由于已知真实分布，可以根据每个高斯分布的概率密度来计算测试样本的错误率。

对于监督学习，忽略无标签数据，决策边界在两个有标记样本的中间，如Training Set 1所示，它远离最佳的决策边界，这是因为两个有标记样本是随机采样的。如果重新随机抽取两个有标签数据，决策边界将会发生变化，但是很可能还是远离最佳决策边界，如其它的粗实线所示。通常，期望学习到一个决策边界与真实的决策边界一致，但是，对于任何给定的标签数据，它都会有所偏差，我们称学习的决策边界存在高方差。

下面将介绍几种常用的半监督学习算法。

半监督学习算法

Self-Training Models

Self-training的特点是学习过程中，利用它自己对无标签数据的预测结果来学习。也就是先使用有标签数据来训练得到一个预测器，然后基于预测器来预测无标签数据，再将所有的有标签数据作为训练数据重新训练。

Algorithm 1. Self-training

输入：有标签数据 {(xi,yi)}li=1 ，无标签数据 {xj}l+uj=l+1
1. 首先，令 L={(xi,yi)}li=1 ， U={xj}l+uj=l+1
2. 重复3,4,5，直到 U 为空
3. 使用监督学习从 L 学习 f 。
4. 将 f 应用到 U 中的无标签数据。
5. 移除 U 的子集 S ；添加 {(x,f(x))|x∈S} 到 L

Self-training的主要思想是先基于有标签数据训练 f ，然后用 f 来预测无标签数据的标签。无标签数据的子集 S (子集 S 的选择可以根据具体情况做调整)，以及它们的预测值，用来增加有标签数据。基于增加后的标签数据重新训练 f ，重复这个过程。

Self-Training Assumption：无标签数据的预测值，至少是高置信度的那些，被认为是正确的。

当类之间能够很好地分开时，上述假设很可能是正确的。

self-training的主要优点是简单，并且是一个包装方法(wrapper method)。也就是步骤3中 f 的选择是任意的，既可以是简单的KNN算法，也可以很复杂的分类器。self-training虽然简单，但是，可能出现 f 早期就出现预测错误的情况(因为一开始 L 比较小，容易造成预测错误)，产生了错误的标签数据。在下一次迭代时，用这些错误数据作为训练样本重新训练会产生一个更差的 f 。目前，有很多的启发式算法来应对这个问题。下面介绍一个具体的self-training的方法。

Algorithm 2. Propagating 1-Nearest-Neighbor

在上述算法中，每一次迭代只选择最靠近标签数据的无标签数据(其中的标签数据有一部分是通过之前的迭代得到的)。

如下图所示，有100个人的身高和体重数据，假设只有两个有标签数据(一男一女)，98个无标签数据，现在需要按性别分类，这里采用Propagating 1-Nearest-Neighbor算法。从图中可以看出，使用该算法得到了很好的结果，这是因为满足不同的类之间能够很好地分开。

下面对数据做略微的修改，引入一个outlier，该outlier落在两个类的中间，如下图所示。由于outlier的存在，使得不同类别的数据能够很好地分开的假设不能满足，最终导致糟糕的结果。很明显，像propagating 1-nearest-neighbor这样的self-training方法对异常点是敏感的，会传播错误信息。避免这个问题的方法是考虑更多的其他信息，而不是只考虑单个最近邻点。

Mixture Models and EM

混合模型的思想是，如果已知每个类中样本的分布情况，可以把混合的分布分解到单个类中。

有监督分类的混合模型

假设训练数据来自两个一维的高斯分布，如下图所示。图中展示了 p(x|y) 的分布及一部分的训练样本，其中只有两个有标记样本。

假设已知数据来自两个高斯分布，但其参数未知(均值、方差、先验概率)。使用有标签数据和无标签数据来估计两个分布的参数。在这个例子中，有标签的数据实际上是会产生误导的，它们都处于真实分布均值的偏右方。但是，无标签数据可以帮助确定两个高斯分布的均值。从计算方面考虑，需要选择参数，使得模型产生训练数据的概率最大。

x∈X 代表一个样本，需要预测该样本的label y 。使用概率的方法来最大化条件概率 p(y|x) ，从而确定label。给定一个样本，该条件概率可以给出该样本属于各个类别的概率，其中 p(y|x)∈[0,1] ， ∑yp(y|x)=1 。

y^=argmaxyp(y|x)

使用贝叶斯公式计算该条件概率

p(y|x)=p(x,y)p(x)=p(x|y)p(y)∑y′p(x|y′)p(y′)

半监督分类的混合模型

在半监督学习中， D 既含有标签数据，又含有无标签数据。似然函数既基于有标签数据，又基于无标签数据。现在，无法直接采用极大似然估计来估计模型参数，因为中间存在隐藏变量，即无标签数据的标签作为隐藏变量，需采用EM算法来求解。

D={(x1,y1),...,(xl,yl),xl+1,...,xl+u} ，对数似然函数为

logp(D|θ)=log⎛⎝∏i=1lp(xi,yi|θ)∏i=l+1l+up(xi|θ)⎞⎠=∑i=1llogp(yi|θ)p(xi|yi,θ)+∑i=l+1l+ulogp(xi|θ)(1)

p(x|θ) 为边缘概率

p(x|θ)=∑y=1Cp(x,y|θ)=∑y=1Cp(y|θ)p(x|y,θ)

称未观测到的标签 yl+1,...,yl+u 为隐藏变量，它们的存在会使得对数似然函数(1)非凸，因此，需要借助EM算法来求解。

EM算法求解

观测数据 D={(x1,y1),...,(xl,yl),xl+1,...,xl+u} ，隐藏数据 H={yl+1,...,yl+u} ，模型参数为 θ 。EM算法通过迭代的方式来得到 θ ，使得 p(D|θ) 取得局部最大值。

Algorithm 3. The Expectation Maximization (EM) Algorithm in General

• q(t)(H) 为隐藏标签的分布。可以认为它是目前模型 θ(t) 赋予无标签数据的soft labels(软标签)。
• EM算法只能收敛到局部最优值。
• EM算法具体收敛到哪个局部最优值，取决于初始化参数 θ(0) 。普遍的做法是选择有标签数据的极大似然估计值。

例：EM for a 2-class GMM with Hidden Variables

对数似然函数

Algorithm 4. EM for GMM

可以看出，EM和self-training存在一定的相似性。EM算法使用当前的分类器 θ ，来给无标签数据打标签，只是计算出的是每个无标签样本属于每个类别的概率，即 p(H|D,θ) ，因此，可以看成是self-training的一个特例。

THE ASSUMPTIONS OF MIXTURE MODELS

Mixture Model Assumption：数据来自混合模型，并且class的数量、先验概率 p(y) 、条件概率 p(x|y) 都是正确的。

由于没有很多的标签数据，所以很难评估模型的正确性。很多时候，生成模型的选择依赖于领域知识和数学知识。如果模型选择错误，半监督学习会影响性能。在这种情况下，只使用有标签数据进行监督学习也许可以得到更好的结果。

例：假设数据集包含四个簇，每个类都由两个簇组成，如下图所示。

正确的决策边界是与 x1 轴平行的线，即 x2=0 ，显然，该数据不是由两个高斯分布产生的。如果我们坚持认为每个类由一个高斯分布产生，会产生错误的结果，如下图所示。在(a)中，可以很好地拟合无标签数据，但是预测误差接近50%。在(b)中，虽然提高了精度，但是EM算法不允许出现这种结果，因为它的对数似然函数偏小。

在这个例子中，如果只使用有标签数据进行监督学习。如果我们只有左下角和右上角的簇中的标签数据，监督学习得到的决策边界接近 y=−x ，预测的错误率也只有25%左右。

有一些方法可以减小由于模型选择错误而导致的风险。一种方案是依赖领域的知识来提炼模型，使得能够更好地拟合当前数据。在上面的例子中，每个类可以使用两个高斯分布来代替之前的一个高斯分布。

另一种方法是减少对无标签数据的重视程度。在对数似然函数中加入权重 λ 来调整无标签数据的权重。

∑i=1llogp(yi|θ)p(xi|yi,θ)+λ∑i=l+1l+ulogp(xi|θ)

当 λ→0 时，无标签数据的影响将消失，半监督转变成有监督。

CLUSTER-THEN-LABEL METHODS

Algorithm 5. Cluster-then-Label

例：还是使用之前的小绿人的数据，如下图所示。在第一步聚类时，采用的是层次聚类法，距离度量采用欧几里得距离。由于标签数据只有两个类，因此当只剩下两个类时，停止聚类。第2-4步，在每个cluster中寻找主要的label，并将该label赋予该cluster。

上面采用的是single linkage来度量类间距的，可以得到很好的结果。但是如果采用complete linkage clustering，会得到下图所示的结果。

Co-Training(协同训练)

考虑自然语言处理中命名实体识别的问题。命名实体指的是专有名词，如“Washington State”、“Mr. Washington”等。根据其指代的东西，每个命名实体都有一个类标签。假设有两个类：Person和Location，命名实体是被的目标是将类标签分配给实体。如将Location分配给Washington State”，将Person分配给“Mr. Washington”。因此，可以将命名实体识别看成是一个分类问题。这里不考虑有监督分类的细节，而是考虑半监督学习。

命名实体可以通过两个特征来表示，一个是命名实体本身 x1 ，另一个是命名实体的上下文 x2 。如下图所示，括号中的是命名实体，下划线的是上下文。

考虑下列样本

1. 从带标签的实例1中，可以学习到如果上下文中有“headquartered in”，似乎意味着 y=Location
2. 如果上面的结论是正确的，则实例3中的 y=Location
3. 实例4同样是关于Kazakhstan的，上下文为“flew to”，意味着 y=Location
4. 对于“flew to (China)”，虽然“flew to”和“China”都没有在标签数据中出现，但是能够将“China”分类为Location
5. 通过匹配实例2和5中的“Mr. *”，可以知道如果上下文是“partner at”，则 y=Persion 。因此，可以将““(Robert Jordan), a partner at”分类为Persion。

这个过程与self-training存在很大的相似性，分类器使用它对未标记实例置信度最高的预测来自学。但是，其中一个关键的不同点是在这里依次使用了两个分类器，其中一个是基于命名实体本身( x(1) )，另一个是基于上下文( x(2) )，这两个分类器互相教导，因此将这个过程称为协同训练的过程。

Algorithm 6. Co-Training.

分类器 f(1) 只考虑特征 x(1) ，不考虑特征 x(2) ，而分类器 f(2) 只考虑特征 x(2) ，不考虑特征 x(1) 。Co-training是一种包装方法，这意味着它对于分类器 f(1) 和 f(2) 的选择没有特定的要求，唯一的要求是分类器能够针对最后的预测结果给定一个概率值。

THE ASSUMPTIONS OF CO-TRAINING

Co-training做了部分假设，其中最明显的一个是存在两个单独的视角 x=[x(1),x(2)] ，一般情况下，有可能不止两个视角。在实际应用中，可以将特征随机拆分成两份。

Co-Training Assumptions

1. 只要有足够的标签数据，单独的一个视角可以得到一个好的分类器
2. 在给定类标签时，这两个视角是条件独立的

对于第二个假设，可以表示为：

P(x(1)|y,x(2))=P(x(1)|y)P(x(2)|y,x(1))=P(x(2)|y)

Graph-Based Semi-Supervised Learning

为了说明基于图的半监督学习方法，这里首先给出一个例子。

Alice正在翻阅一本杂志“Sky and Earth”，上面的文章要么是关于天文学(astronomy)的，要么是关于旅行(travel)的。Alice不认识英语，只能从每篇文章的图片中猜测该文章的主题。第一个故事“Bright Asteroid”的图片展示了一个多坑的小行星，显然它是关于天文学的。第二个故事“Yellowstone Camping”的图片展示了一只灰熊，她认为它一定是关于旅行的。

但是，剩下的其他文章只有文字，没有展示图片。第三篇文章的标题为“Zodiac Light”，第四篇文章的标题为“Airport Bike Rental”。Alice不认识单词，文章又没有图片，看起来不可能猜测文章的主题。

不过，Alice是一个聪明的孩子，她注意到其它文章的标题为“Asteroid
and Comet”，“Comet Light Curve”，“Camping in Denali”，“Denali Airport”。Alice想：我假设如果两个标题存在相同的词，那么这两篇文章属于同一个主题。因此，Alice得出了下图的结果：

可以看到，Alice得到了正确的结果，她无意识地使用到了基于图的半监督学习方法。

THE GRAPH

基于图的半监督学习首先得基于训练数据构建一个图。给定训练数据 {(xi,yi)}li=1 ， {xj}l+uj=l+1 ，顶点为有标签数据和无标签数据 {(xi)}li=1∪{xj}l+uj=l+1 。如果无标签数据的数据量很大，那构建的图会很大。一旦图被建立，将会学习如何给图中的顶点分配 y 值，这可以通过有标签数据和无标签数据相连接的边来判断。图中的边通常是没有方向的，其权重为 wij 。其中的思想是 wij 越大，label yi 和 yj 相同的可能性越大。因此，边的权重在图中是非常重要的，通常有以下几种指定边权重的方法：

• 对于全连接图，即对于任意两个顶点 xi 和 xj 都有边将它们相连。当它们的欧几里得距离增大时，它们之间边的权重相应减小。其中一个通用的权重函数为

wij=exp(−||xi−xj||22σ2)(2)

其中， σ 用来决定权重减小的速率。该权重与高斯函数的形式是一样的，因此也被称为高斯核或者径向基(RBF)核。若 xi=xj ，则权重为1；若 ||xi−xj||2 趋向于无穷大时，权重为0。

• kNN图。基于欧几里得距离定义每个顶点的k个最近邻顶点。注意，如果 xi 是 xj 的k近邻，反过来不一定成立，即 xj 不一定是 xi 的k近邻。如果 xi,xj 其中一个是另一个的k近邻，则将它们通过边连接起来，这意味着每个顶点可能有多余k条边。如果 xi,xj 是相连的，边的权重 wij 可以设定为1(图为无权图)，或者可以按照(2)式来设置权重。KNN图在特征空间中能够自动适应样本的密度，在样本密集区域，k个邻居的半径范围较小，在稀疏区域，则半径范围较大。一般地，k值较小时效果较好。

• ϵ NN图。如果 ||xi−xj||≤ϵ ，则将 xi,xj 相连。边可以有权重，也可以没有权重。

以上这些都是通用的方法，如果有专业的知识，则可以构造更专业的图，可以定义更好的距离函数、连接以及权重。

如下图所示，其中的边是稀疏的， x1,x2 为两个有标签样本(顶点)。如上所述，若假设存在边连接意味着具有相同的label，对于无标签数据 x3 ，它的label y3 与它的邻居是相似的，也跟它的邻居的邻居相似，因此 y3 更相似于 y1 。实际上， x3 与 x2 的欧几里得距离更小，如果没有图，我们会认为 y3 更相似于 y2 。

MINCUT

首先介绍一个关于图的最小分割方法。它的主要思想是：在二分类问题中，定义正例数据作为源点(source)，就像液体顺着边从它们流出，负例样本视为汇点(sink)，液体将在它们这边停止。目标是寻找边的最小集合，使得删除该边集之后能够隔绝任意从源点到汇点的流量。这里定义了一个切割“cut”，也就是将图的顶点分为两个集合。cut size定义为切割边的权重之和。一旦图被切割，则与source节点相连的节点打上正标签，与sink节点相连的节点打上负标签。

用数学的方式来阐述，即找到一个函数 f(x)∈{−1,1} ，对于所有标签数据， f(xi)=yi 。最小化cat size

∑i,j:f(xi)≠f(xj)wij

由上式可以看出，如果边 wij 被移除，一定满足 f(xi)≠f(xj) 。

现在考虑正则化风险最小问题。对于任何有标签节点 xi ， f 需满足 f(xi)=yi 。可以定义损失函数

c(x,y,f(x))=∞⋅(y−f(x))2

cut size可以写成

Ω(f)=∑i,j=1l+uwij(f(xi)−f(xj))2/4

上式是对所有的顶点组合进行求和。如果 xi 和 xj 没有连接，则 wij=0 。如果边存在但是没有被切割，则 f(xi)−f(xj)=0 。Mincut损失函数定义为

minf:f(x)∈{−1,1}∞∑i=1l(yi−f(xi))2+∑i,j=1l+uwij(f(xi)−f(xj))2

因为 f(x)∈{−1,1} ，所以这是一个整数规划问题。

上述的Mincut可能存在多个最优解，如下图所示。图中有两个有标签的顶点，正顶点和负顶点分别位于链的两端，且所有的边都具有相同的权重，如 ϵ NN图。则存在6个Mincut解：移除任意一条边都可以分离正负两个顶点，使得cut size最小。但是，中间还存在置信度的问题，实际上并不是6个解都是最优的。

HARMONIC FUNCTION(调和函数)

现在介绍第二种基于图的半监督学习算法——调和函数，它将预测函数从离散形式扩展到连续形式，其满足以下条件

f(xi)f(xj)=yi,i=1,...,l=∑l+uk=1wjkf(xk)∑l+uk=1wjk,j=l+1,...,l+u

即调和函数为：对于有标签数据，调和函数的值与标签值相等，对于无标签数据，调和函数的值为权重的加权平均值，也就是无标签数据的调和函数值等于它邻居值的加权平均。它的目标是

minf:f(x)∈R∞∑i=1l(yi−f(xi))2+∑i,j=1l+uwij(f(xi)−f(xj))2

等同于下列有约束的优化问题，即

minf:f(x)∈Rsubject to ∑i,j=1l+uwij(f(xi)−f(xj))2f(xi)=yi,i=1,...,l

现在存在封闭解 f ，该解是全局最优的。但现在 f(x) 是在区间 [−1,1] 中的实数，不能直接对应到标签。不过，可以通过阈值转换将它转换成-1和1，如：如果 f(x)≥0 ，则 y=1 ；如果 f(x)<0 ，则 y=−1 。

THE ASSUMPTION OF GRAPH-BASED METHODS

Graph-Based Semi-Supervised Learning Assumption：如果两个样本之间通过高权重的边相连，则它们的标签倾向于相同。

Semi-Supervised Support Vector Machines

这里只对半监督支持向量机做简单介绍，详细内容请参考博客：http://blog.csdn.net/extremebingo/article/details/79020907

直观上，半监督支持向量机Semi-Supervised Support Vector Machines (S3VMs)是很简单的，如下图所示。 图(a)展示了完整标记的数据集(SVM的理论和思想这里不做详细介绍)及其分离超平面。如果除了有标签数据，另外还存在着一些无标签数据，分布情况如图(b)所示，那分离超平面该如何确定呢？

如果数据是可分的，那么似乎分离超平面不应该穿过稠密的无标签数据，而应该是图中实线所示的分离超平面，该分离超平面落在无标签数据的间隙中，并且同样可以将有标签数据有效地分开，只是决策边界的宽度有所减小。图(b)所示的决策边界即所谓的S3VMs。

THE ASSUMPTION OF S3VMS

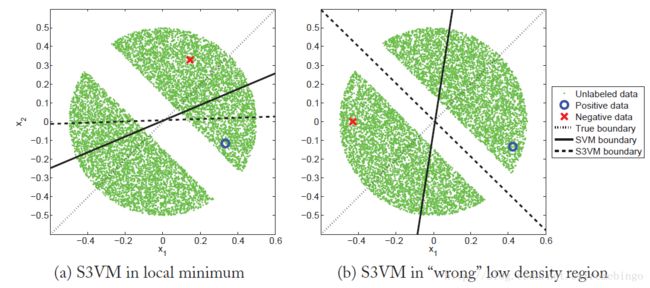
S3VMs Assumption：不同的类时可分的，在特征空间中，决策边界落在低密度区域。

如果数据不满足假设，则可能造成糟糕的分类结果，如下图所示。

参考文献

[1] Zhu, Xiaojin, and Andrew B. Goldberg. “Introduction to semi-supervised learning.” Synthesis lectures on artificial intelligence and machine learning 3.1 (2009): 1-130.
[2] 刘建伟, 刘媛, 罗雄麟. 半监督学习方法[J]. 计算机学报, 2015(8):1592-1617.
[3] 梁吉业, 高嘉伟, 常瑜. 半监督学习研究进展[J]. 山西大学学报(自然科学版), 2009, 32(4):528-534.