深度学习（Deep Learning）读书思考六：循环神经网络一（RNN）

概述

循环神经网络（RNN-Recurrent Neural Network）是神经网络家族中的一员，擅长于解决序列化相关问题。包括不限于序列化标注问题、NER、POS、语音识别等。RNN内容比较多，分成三个小节进行介绍，内容包括RNN基础以及求解算法、LSTM以及变种GRU、RNN相关应用。本节主要介绍

1.RNN基础知识介绍
2.RNN模型优化以及存在的问题
3.RNN模型变种

RNN知识点

RNN提出动机

RNN的提出可以有效解决以下问题：

1. 长期依赖问题：在语言模型、语音识别中需要根据上下文进行推断和预测，上下文的获取可以根据马尔科夫假设获取固定上下文。RNN可以通过中间状态保存上下文信息，作为输入影响下一时序的预测。

2. 编码：可以将可变输入编码成固定长度的向量。和CNN相比，能够保留全局最优特征。

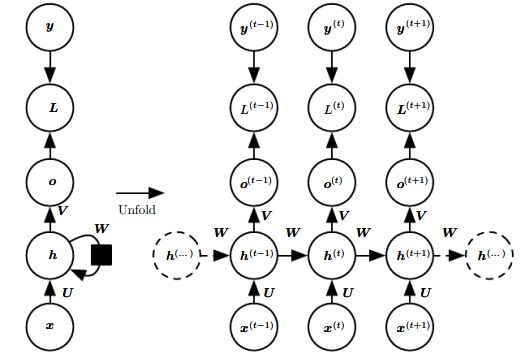
   计算图展开

   RNN常用以下公式获取历史状态

   ht=f(ht−1,xt;θ)
   
   其中h为隐藏层，用于保存上下文信息，f是激活函数。
   用图模型可以表达为：
   

RNN潜在可能的展开方式如下：
1）通过隐藏层传递信息

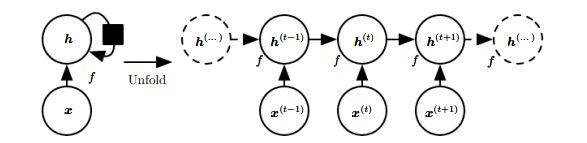
1.该展开形式非常常用，主要包括三层输入-隐藏层、隐藏层-隐藏层、隐藏层到输入层。依赖信息通过隐藏层进行传递。
2.参数U、V、W为共享参数

2）输出节点连接到下一时序序列

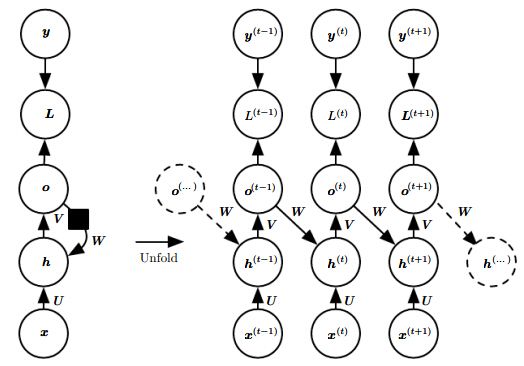
应用比较局限，上一时序的输出作为下一时间点的输入，理论上上一时间点的输出比较固定，能够携带的信息比较少。

3）只有一个输出节点

只在最后时间点t产生输出，往往能够将变成的输入转换为固定长度的向量表示。

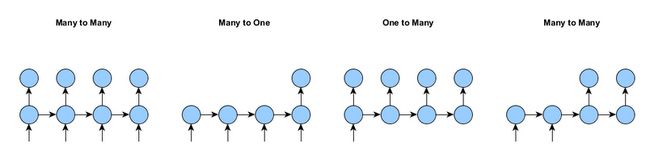
RNN使用形式

在使用RNN时，主要形式有4中，如下图所示。

1.一对一形式（左一：Many to Many）每一个输入都有对应的输出。
2.多对一形式（左二：Many to one）整个序列只有一个输出，例如文本分类、情感分析等。
3. 一对多形式（左三：One to Many）一个输入产出一个时序序列，常用于seq2seq的解码阶段
4.多对多形式（左四：Many to Many）不是每一个输入对应一个输出，对应到变成的输出。

RNN数学表达以及优化

RNN前向传播

对于离散时间的RNN问题可以描述为，输入序列

(x1,y1),(x2,y2),(x3,y3)......(xT,yT)

其中时间参数t表示离散序列，不一定是真实时间点。
对于多分类问题，目标是最小化释然函数

min∑t=1TL(y^(xt),yt)=min−∑tlog p(yt|x1,x2...xt)

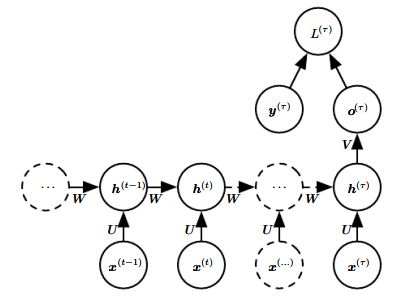
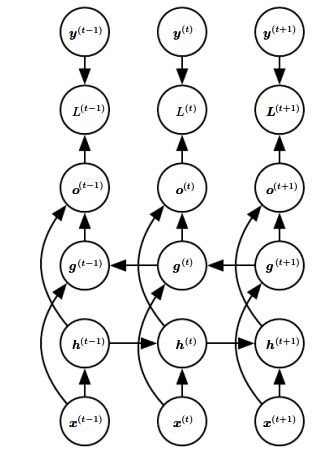
根据上面经典的RNN网络结构，前向传播过程如下：
如上图U、V、W分别表示输入到隐藏层、隐藏层到输出以及隐藏到隐藏层的连接参数。
1. 隐藏层节点权值： at=b+Wht−1+Uxt
2. 隐藏层非线性变换: ht=tanh(at)
3. 输出层： ot=c+Vht
4. softmax层： y^t=softmax(ot)

RNN优化算法-BPTT

BPTT 是求解RNN问题的一种优化算法，也是基于BP算法改进得到和BP算法比较类似。为直观上理解通过多分类问题进行简单推导。
1. 优化目标，对于多分类问题，BPTT优化目标转换最小化交叉熵：

min∑tLtLt=−∑kytklogy^tk

这里假设有k个类
2. 由于总的损失L为各个时序点的损失和，因此有

∂L∂Lt=1

3. 对于输出层中的第i节点有

(∇otL)i=∂L∂oti=∂L∂Lt∂Lt∂oti=y^ti−1i,yt

最后一步是交叉熵推导结果，步骤省略，了解softmax的都清楚。 1i,yt 表示如果y^t==i则为1，否则为0
4. 隐藏层节点梯度的计算，分为两部分，第一部分 t=T。

(∇hTL)i=∑j(∇oTL)j∂oTj∂hTi=∑j(∇oTL)jVij

通过向量的方式表达为

(∇hTL)=(∇oTL)∂oT∂hT=(∇oTL)V

5.第二部分， 中间节点 t<T ，对于中间节点需要考虑t+1以及以后时间点传播的误差，因此计算过程如下。

(∇htL)i=∑j(∇ht+1L)j∂ht+1j∂hti+∑k(∇otL)k∂otk∂hti=隐藏层误差反馈+输出层误差反馈=∑j(∇ht+1L)j∂ht+1j∂at+1j∂at+1j∂hti+∑k(∇otL)kVki=∑j(∇ht+1L)j(1−ht+1j2)Wji+∑k(∇otL)kVki=(∇ht+1L)diag((1−ht+12))Wi+(∇otL)Vi

通过向量表示如下：

(∇htL)=(∇ht+1L)∂ht+1∂ht+(∇otL)∂ot∂ht=(∇ht+1L)diag((1−ht+12))W+(∇otL)V

其中 diag((1−ht+12)) 是由 1−ht+1i 的平方组成的对角矩阵。
6.根据中间结果的梯度可以推导出其他参数的梯度，结果如下

∇cL∇bL∇VL∇WL∇UL=∑t(∇toL)∂ot∂c=∑t(∇toL)=∑t(∇thL)∂ht∂b=∑t(∇thL)diag((1−ht2))=∑t(∇toL)∂ot∂V=∑t(∇toL)htT=∑t(∇thL)∂ht∂W=∑t(∇thL)diag((1−ht2))ht−1T=∑t(∇thL)∂ht∂U=∑t(∇thL)diag((1−ht2))xtT

7. 到此完成了对所有参数梯度的推导。

梯度弥散和爆炸问题

RNN训练比较困难，主要原因在于隐藏层参数W，无论在前向传播过程还是在反向传播过程中都会乘上多次。这样就会导致1）前向传播某个小于1的值乘上多次，对输出影响变小。2）反向传播时会导致梯度弥散问题，参数优化变得比较困难。

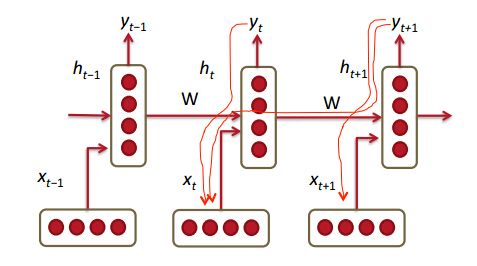
可以通过梯度公式也可以看出梯度弥散或者爆炸问题。
考虑到通用性，激活函数采用f(x)代替，则对隐藏层到隐藏层参数W梯度公式如下：

∇WL=∑t(∇thL)∂ht∂W=∑t(∇thL)diag(f′(ht))ht−1

后面部分可以直接得到，下面详细分析它的系数 (∇thL)

1.考虑当t=T，即为最后一个节点时，根据上面的推导有

(∇hTL)=(∇oTL)∂oT∂hT=(∇oTL)V

2.当t=T-1时，

(∇hT−1L)=(∇ThL)∂ht+1∂ht=(∇hTL)diag(f′(hT))W

注这里只考虑隐藏层节点对W的误差传递，没有考虑输出层。
3. 当t=T-2时，

(∇hT−2L)=(∇T−1hL)∂hT−1∂hT−2=(∇hTL)diag(f′(hT))Wdiag(f′(hT−1))W=(∇hTL)diag(f′(hT))diag(f′(hT−1))W2

4. 当t=k时

(∇hkL)=(∇ThL)∏j=k+1T∂hj∂hj−1=(∇hTL)∏j=kTdiag(f′(hj))W

5.此时 diag(f′(hj))W 的结果是一个对角矩阵，如果其中某个元素大于1，则该值会指数倍放大；否则会以指数倍缩小。
6.因此可以看出当序列比较长，即模型有长期依赖问题时，就会产生梯度相关问题。一般情况下BPTT对于序列长度在100以内，不会暴露问题。
7.需要注意的是，如果我们的训练样本被人工分为子序列，且长度都较小时，不会产生梯度问题。此时比较依赖于前期预处理

梯度问题解决方案

梯度爆炸问题方案

该问题采用截断的方式有效避免，并且取得较好的效果。

梯度弥散问题解决方案

针对该问题，有大量的解决方法，效果不一致。
1.有效初始化+ReLU激活函数能够得到较好效果
2.算法上的优化，例如截断的BPTT算法。
3.模型上的改进，例如LSTM、GRU单元都可以有效解决长期依赖问题。
4.在BPTT算法中加入skip connection，此时误差可以间歇的向前传播。
5.加入一些Leaky Units，思路类似于skip connection

RNN模型改进

主要有两大类思路

双向RNN（Bi-RNN）

此时不仅可以依赖前面的上下文，还可以依赖后面的上下文。

深度RNN（Deep-RNN）

有多种方式进行深度RNN的组合，左一比较常用。

总结

通过该小结的总结，可以了解到
1）RNN模型优势以及处理问题形式。
2）标准RNN的数学公式以及BPTT推导
3）RNN模型训练中的梯度问题以及如何避免