- 【华为OD机试真题2023B卷 JAVA&JS】We Are A Team
若博豆
java算法华为javascript
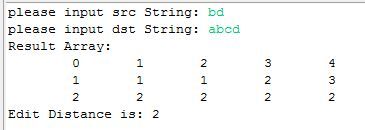
华为OD2023(B卷)机试题库全覆盖,刷题指南点这里WeAreATeam时间限制:1秒|内存限制:32768K|语言限制:不限题目描述:总共有n个人在机房,每个人有一个标号(1<=标号<=n),他们分成了多个团队,需要你根据收到的m条消息判定指定的两个人是否在一个团队中,具体的:1、消息构成为:abc,整数a、b分别代
- 【华为OD技术面试真题 - 技术面】- python八股文真题题库(4)
算法大师
华为od面试python
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例:文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片(Slicing)操作**基本切片语法
- 【华为OD技术面试真题 - 技术面】-测试八股文真题题库(1)
算法大师
华为od面试python算法前端
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.黑盒测试和白盒测试的区别2.假设我们公司现在开发一个类似于微信的软件1.0版本,现在要你测试这个功能:打开聊天窗口,输入文本,限制字数在200字以内。问你怎么提取测试点。功能测试性能测试安全性测试可用性测试跨平台兼容性测试网络环境测试3.接口测试的工具你了解哪些
- 【华为OD技术面试真题 - 技术面】- python八股文真题题库(1)
算法大师
华为od面试python
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归(LinearRegression)模型形式:关键点:逻辑回归(LogisticRegression)模型形式:关键点:参数估计与评估:3.python浅拷贝及深拷贝浅拷贝(Shal
- 2024.9.6 Python,华为笔试题总结,字符串格式化,字符串操作,广度优先搜索解决公司组织绩效互评问题,无向图
RaidenQ
python华为leetcode算法力扣广度优先无向图
1.字符串格式化name="Alice"age=30formatted_string="Name:{},Age:{}".format(name,age)print(formatted_string)或者name="Alice"age=30formatted_string=f"Name:{name},Age:{age}"print(formatted_string)2.网络健康检查第一行有两个整数m
- 2019考研 | 西交大软件工程
笔者阿蓉
本科背景:某北京211学校电子信息工程互联网开发工作两年录取结果:全日制软件工程学院分数:初试350+复试笔试80+面试85+总排名:100+从五月份开始脱产学习,我主要说一下专业课和复试还有我对非全的一些看法。【数学100+】张宇,张宇,张宇。跟着张宇学习,入门视频刷一遍,真题刷两遍,错题刷三遍。书刷N多遍。从视频开始学习,是最快的学习方法。5-7月份把主要是数学学好,8-9月份开始给自己每个周
- 2021年化工自动化控制仪表考试及化工自动化控制仪表考试技巧
女王219
安全生产模拟考试一点通安全生产一点通题库
题库来源:安全生产模拟考试一点通公众号小程序化工自动化控制仪表考试参考答案及化工自动化控制仪表考试试题解析是安全生产模拟考试一点通题库老师及化工自动化控制仪表操作证已考过的学员汇总,相对有效帮助化工自动化控制仪表考试技巧学员顺利通过考试。1、【单选题】辐射传热()任何介质做媒介。(A)A、不需要B、需要C、有时需要2、【单选题】同一密度的液体深度越深,压强()。(B)A、越小B、越大C、基本不变3
- 算法笔试-编程练习-好题-05
Glen 997
大厂校招-编程集训算法动态规划双指针
【题目类型:动规+双指针】题目内容有N个基站采用链式组网,按照从左到右编码为1到N编号。已知定义“业务”概念为三元组(基站起始编号,基站结束编号,利润),意味着需要占据基站起始编号到基站结束编号的所有基站,打通信号流,可以获得对应利润。现在外部存在多个“业务"需求待接纳,但基站使用具有排他性,也就是说一旦某一个业务占据某个基站,其他业务不可以再使用此基站。那么接纳哪些业务需求,可以使得利润最大化?
- 算法笔试-编程练习-好题-04
Glen 997
大厂校招-编程集训算法大厂笔试动态规划堆盒子
题目:堆盒子礼盒大小不同,我们玩堆盒子的游戏,怎么堆盒子使得堆出的高度最高,每个礼盒的大小由长、宽、高表示,堆盒子的时候要求下面的盒子长、宽、高都必须大于上面的盒子,不包含等于。高度为堆出的礼盒的所有高度的总和。输入描述输入的第一行是礼盒的个数N,接下来输入N行,每行表示每个礼盒的长、宽、高。礼盒的数量不超过1000个,每个盒子的长、宽、高取值范围为1~10。输出描述输出一行,输出能堆出盒子的最高
- 数据库常见笔试面试题及其解析
yxsr_zxx
数据库数据库SqlServerOracle笔试面试
数据库基础(面试常见题)一、数据库基础1.数据抽象:物理抽象、概念抽象、视图级抽象,内模式、模式、外模式2.SQL语言包括数据定义、数据操纵(DataManipulation),数据控制(DataControl)数据定义:CreateTable,AlterTable,DropTable,Craete/DropIndex等数据操纵:Select,insert,update,delete,数据控制:g
- 【华为OD机试真题 python】输出指定字母在字符串的中的索引【2022 Q4 | 100分】
无痕de泪
华为OD机试真题python输出指定字母在字符串的中的索引字符串华为odpython
前言《华为OD笔试真题python》专栏含华为OD机试真题、华为面试题、牛客网华为专栏真题。如果您正在准备华为的面试,或者华为od的机会,有任何想了解的可以私信我进行交流。我会尽可能的给一些建议,和帮您解答!PS:文中答案仅供参考,不能照抄哦■题目描述【输出指定字母在字符串的中的索引】给定一个字符串,把字符串按照大写在前小写在后排序,输出排好后的第K个字母在原来字符串的索引。相同字母输出第一个出现
- 大数据真实面试题---SQL
The博宇
大数据面试题——SQL大数据mysqlsql数据库bigdata
视频号数据分析组外包招聘笔试题时间限时45分钟完成。题目根据3张表表结构,写出具体求解的SQL代码(搞笑品类定义:视频分类或者视频创建者分类为“搞笑”)1、表创建语句:createtablet_user_video_action_d(dsint,user_idstring,video_idstring,action_typeint,`timestamp`bigint)rowformatdelimi
- 伦理考试
伊世界
“今天开始首轮关于伦理的考核。时间:上午9:00及下午14-00开始方式:笔试要求:1、私信下发word文件,请在开始后的1.5小时内答完并发回。2、答题间请勿查阅相关资料。3、各位老师间请勿转发。”好好准备一下“相关资料和文件。”有些人,光是遇见,就足够惊艳我们整个时光。老话常说:“珍宝易求,良人难得。”婚姻的最大意义,不仅仅是一日三餐、同枕而眠,而是用一个灵魂去成全另一个灵魂,彼此滋养、彼此奔
- 特种作业操作登高架设题库
安建资小栗子
其他
1.带电跨越架宜采用干燥的竹竿、杉杆搭设,严禁使用()等。A.钢管B.松木C.柳木答案:A2.跨越架立杆间距为()m。A.1.2B.1.5C.1.8答案:B3.跨越架杆件相交时,不得一扣绑()根。A.2B.3C.4答案:B4.下列哪种形式的脚手架不得作为承重脚手架()。A.扣件式钢管B.杉槁C.碗扣式钢管答案:B5.单排脚手架横向水平杆插入墙内长度不应小于()㎜。A.100B.150C.180答案
- 上海安全员C证继续教育题库(附答案)
安建资小栗子
其他
1.从业人员经过安全教育培训,了解岗位操作规程,但未遵守而造成事故的,行为人应负()责任,有关负责人应负()责任。A.直接间接B.直接领导C.间接管理D.直接管理2.对生产附着式升降脚手架产品的单位,必须经()组织鉴定合格并发给生产和使用证后,方可向全国各地提供产品。A.国家安全监督总局B.国家质量监督总局C.住房和城乡建设部D.当地建设行政主管部门3.建筑施工进行高处作业之前,应进行安全防护设施
- 笔记22 追求安全感
玩命凯旋
我的一个同学刚考了今年的国家公务员,笔试成绩出来了,他进入面试名额了,现在一直在做面试相关的准备。看到他的这种状态,再想想公务员的福利待遇也很好,我内心也产生了考公务员的强烈想法,这或许是在外漂泊久了想回家过安定生活,也或许是好多同学都考上了很羡慕他们!重庆每年有两次考试机会,再加上国考,一年共三次!今天看了好多关于安全感的评论,很多同学身在体制中,表示工作相当乏味没有激情,除了安全没有其他任何好
- 【免费刷题】实验室安全第一知识题库分享
打工要不要摸鱼
安全
道路千万条,实验安全第一条。嘿,实验室的小伙伴们!是不是还在为实验室安全考试而烦恼?别担心,今天就让我来分享一些实用的题库,帮助你轻松应对考试,同时也更好地保护自己和实验室的安全。一、为什么要注意实验室安全?实验室是进行实验教学和科学研究的重要基地,实验室安全不仅关系到我们自身的生命健康,还关系到实验室财产的安全。一个小小的疏忽,就可能导致大大的事故。所以,我们要时刻牢记“安全第一,预防为主”。举
- 公务员入职路上,那些温暖的时刻
就上岸
个人简介:职场辣妈,在职带娃考公,成功上岸。如果你正在迷茫是否考公务员,或者在备考的过程中有困惑,都欢迎找我交流。能够一路顺顺利利的走过公务员考试的笔试、面试、体检、政审,上岸成功。我觉得,自己是一个幸运的人。幸运一,一个已经上岸的朋友,毫无保留的教给我他的申论心得,助我找到了申论的突破点。幸运二,一起的复习的小伙伴,真诚的帮助彼此。幸运三,在上午的行测考试结束,感觉极其挫败的情况下,没有任性的放
- 2018农信社备考知识点精选:多定义判断
云南华图金领人
农信社笔试中判断推理-定义判断-多定义判断怎么击破,华图农村信用社招聘网为你解答。A.如果我发挥得稍微差一点,就与奖牌失之交臂了知识点:判断推理-定义判断-多定义判断知识点详解:多定义判断的做题方法:在题干定位所提问的定义,再运用单定义判断的方法,寻找要件,提取关键信息,对比选项。要件主体:定义的发出者,是实践活动和认识活动的承担者,与定义相符的选项的主体应该与定义的主体一致。客体:主体行为所指向
- 《第一红人》钟德兴于欣然(完整版小说)全文在线阅读
小说推书
《第一红人》钟德兴于欣然(完整版小说)全文在线阅读主角:钟德兴于欣然简介:大学毕业后,钟德兴一边在姐姐的水果店卖水果,一边考公。结果,连考了几年都没考上。这年,他再次考公,笔试拿了第一却险些被刷下。幸得贵人帮助,得以成功,人生从此开挂……可关注微信公众号【风车文楼】去回个书号【202】,即可免费阅读【第一红人】全文!“这位同志,是这么回事!”方超平解释说,“我是县蔬菜公司的,这人和他姐租我们公司的
- 【Py/Java/C++三种语言OD独家2024E卷真题】20天拿下华为OD笔试之【链表】2024E-寻找链表的中间节点【欧弟算法】全网注释最详细分类最全的华为OD真题题解
闭着眼睛学算法
最新华为OD真题#链表#双指针javac++华为odpython算法leetcode
可上欧弟OJ系统练习华子OD、大厂真题绿色聊天软件戳od1441了解算法冲刺训练(备注【CSDN】否则不通过)文章目录相关推荐阅读题目描述与示例题目描述输入描述输出描述示例一输入输出说明示例二输入输出说明解题思路邻接表储存链表链表节点的前进解法一:用列表储存所有链表节点数据解法二:快慢双指针代码解法一(数组解法)pythonjavacpp时空复杂度解法二(双指针解法)pythonjavacpp时空
- 2019年面试遇到的笔试题
程序猿阿峰
前端面试,肯定是少不了笔试题,果然,今天去面试就遇到的笔试题,慌了一批。回来赶紧整理了一下一、css3的常用的新特性?flex布局和传统布局有什么区别?css3的新特性那就多啦,简单的列举了几个:过渡transition:CSS属性,花费时间,效果曲线(默认ease),延迟时间(默认0)动画animation:动画名称,一个周期花费时间,运动曲线(默认ease),动画延迟(默认0),播放次数(默认
- 2021-04-06笔试
嘿_叫我小王
1.用图画出产品研发周期中软件测试的不同阶段,并加以适当描述单元测试、集成测试、系统测试、验收测试单元测试:系统最小可测试的单元集成测试:将各个单元连接起来,穿插接口数据是否受到影响系统测试:范围包括--功能测试,ui测试,性能测试,兼容性测试,用户体验测试,安装测试,文档测试,稳定性测试验收测试:在UAT测试之前,指定测试方案,选用基线测试,即最高级别的测试。在UAT测试环境上进行测试,如果通过
- 卷到怀疑人生!一屋子人都在做Java笔试
小坏讲微服务
java面试求职招聘springboot
卷到怀疑人生!一屋子人都在做Java笔试、请大家推荐下转发下我的视频帮助更多的人避坑说明一下这家公司超级坑货、早上10点-晚上8点面试,几个小时笔试二三十个人、在一间没有空调的房间里、热死了二三十个人在一起写、完全像是被喊过来浪费时间啊、还是周日愉快的时光被这个智障公司给浪费了希望大家都不要被这家骗过去刷KPI、希望大家看见直接拉黑啊、卷到怀疑人生!一屋子人都在做Java笔试
- Python基础知识进阶之正则表达式_头歌python正则表达式进阶
前端陈萨龙
程序员python学习面试
最后硬核资料:关注即可领取PPT模板、简历模板、行业经典书籍PDF。技术互助:技术群大佬指点迷津,你的问题可能不是问题,求资源在群里喊一声。面试题库:由技术群里的小伙伴们共同投稿,热乎的大厂面试真题,持续更新中。知识体系:含编程语言、算法、大数据生态圈组件(Mysql、Hive、Spark、Flink)、数据仓库、Python、前端等等。网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是
- [C高手编程] 自增自减/三目运算符/运算符优先级/强制类型转换:表达式与操作全面解析
极客代码
c语言开发语言自增三目运算符强制类型转换自减
⚡️⚡️专栏:C高手编程-面试宝典/技术手册/高手进阶⚡️⚡️「C高手编程」专栏融合了作者十多年的C语言开发经验,汇集了从基础到进阶的关键知识点,是不可多得的知识宝典。如果你是即将毕业的学生,面临C语言的求职面试,本专栏将帮助你扎实地掌握核心概念,轻松应对笔试与面试;如果你已有两三年的工作经验,专栏中的内容将补充你在实践中可能忽略的新技术和技巧;而对于资深的C语言程序员,这里也将是一本实用的技术备
- 数学建模笔记——动态规划
liangbm3
数学建模笔记数学建模笔记动态规划python背包问题算法优化问题
数学建模笔记——动态规划动态规划1.模型原理2.典型例题2.1例1凑硬币2.2例2背包问题3.python代码实现3.1例13.2例2动态规划1.模型原理动态规划是运筹学的一个分支,通常用来解决多阶段决策过程最优化问题。动态规划的基本想法就是将原问题转换为一系列相互联系的子问题,然后通过逐层地推来求得最后的解。目前,动态规划常常出现在各类计算机算法竞赛或者程序员笔试面试中,在数学建模中出现的相对较
- 国内PMP可以在线考试?
胡杨学长.
pmp项目管理项目经理2024年职场证书PMP证书机考
1.PMP考试的两种类型PMP®考试分为两种类型:一种是在线机考,另一种是线下笔试。国外采用机考形式,可以随时参加考试,除了节假日;而国内由中国国际人才交流基金会和PMI共同组织,因此是线下笔试。虽然线上考试和传统的线下考试有所不同,但它们都是经过授权和规范的考试,具有相同的标准和要求。在很多方面,线上考试比传统的线下考试更具优势,比如更方便快捷的考试安排、更灵活的考试时间和地点、更低的考试成本等
- 牛客小白月赛99(上)
筱姌
牛客比赛算法c++
材料打印题目描述登录—专业IT笔试面试备考平台_牛客网运行代码#includeusingnamespacestd;intmain(){intT;cin>>T;while(T--){longlonginta,b,x,y;cin>>a>>b>>x>>y;if(x>T读取测试数据组数T。在循环中,使用cin>>a>>b>>x>>y依次读取每组测试数据中的四个整数,分别代表可黑白或彩印的页数a、必须彩印的
- 牛客周赛 Round 58(下)
筱姌
算法
能做到的吧题目描述登录—专业IT笔试面试备考平台_牛客网运行代码#include#includeusingnamespacestd;stringfindMax(strings){intn=s.length();stringans=s;for(inti=0;ians)ans=s;swap(s[i],s[j]);}}returnans;}intmain(){intt;cin>>t;while(t--)
- web报表工具FineReport常见的数据集报错错误代码和解释
老A不折腾
web报表finereport代码可视化工具
在使用finereport制作报表,若预览发生错误,很多朋友便手忙脚乱不知所措了,其实没什么,只要看懂报错代码和含义,可以很快的排除错误,这里我就分享一下finereport的数据集报错错误代码和解释,如果有说的不准确的地方,也请各位小伙伴纠正一下。
NS-war-remote=错误代码\:1117 压缩部署不支持远程设计
NS_LayerReport_MultiDs=错误代码
- Java的WeakReference与WeakHashMap
bylijinnan
java弱引用
首先看看 WeakReference
wiki 上 Weak reference 的一个例子:
public class ReferenceTest {
public static void main(String[] args) throws InterruptedException {
WeakReference r = new Wea
- Linux——(hostname)主机名与ip的映射
eksliang
linuxhostname
一、 什么是主机名
无论在局域网还是INTERNET上,每台主机都有一个IP地址,是为了区分此台主机和彼台主机,也就是说IP地址就是主机的门牌号。但IP地址不方便记忆,所以又有了域名。域名只是在公网(INtERNET)中存在,每个域名都对应一个IP地址,但一个IP地址可有对应多个域名。域名类型 linuxsir.org 这样的;
主机名是用于什么的呢?
答:在一个局域网中,每台机器都有一个主
- oracle 常用技巧
18289753290
oracle常用技巧 ①复制表结构和数据 create table temp_clientloginUser as select distinct userid from tbusrtloginlog ②仅复制数据 如果表结构一样 insert into mytable select * &nb
- 使用c3p0数据库连接池时出现com.mchange.v2.resourcepool.TimeoutException
酷的飞上天空
exception
有一个线上环境使用的是c3p0数据库,为外部提供接口服务。最近访问压力增大后台tomcat的日志里面频繁出现
com.mchange.v2.resourcepool.TimeoutException: A client timed out while waiting to acquire a resource from com.mchange.v2.resourcepool.BasicResou
- IT系统分析师如何学习大数据
蓝儿唯美
大数据
我是一名从事大数据项目的IT系统分析师。在深入这个项目前需要了解些什么呢?学习大数据的最佳方法就是先从了解信息系统是如何工作着手,尤其是数据库和基础设施。同样在开始前还需要了解大数据工具,如Cloudera、Hadoop、Spark、Hive、Pig、Flume、Sqoop与Mesos。系 统分析师需要明白如何组织、管理和保护数据。在市面上有几十款数据管理产品可以用于管理数据。你的大数据数据库可能
- spring学习——简介
a-john
spring
Spring是一个开源框架,是为了解决企业应用开发的复杂性而创建的。Spring使用基本的JavaBean来完成以前只能由EJB完成的事情。然而Spring的用途不仅限于服务器端的开发,从简单性,可测试性和松耦合的角度而言,任何Java应用都可以从Spring中受益。其主要特征是依赖注入、AOP、持久化、事务、SpringMVC以及Acegi Security
为了降低Java开发的复杂性,
- 自定义颜色的xml文件
aijuans
xml
<?xml version="1.0" encoding="utf-8"?> <resources> <color name="white">#FFFFFF</color> <color name="black">#000000</color> &
- 运营到底是做什么的?
aoyouzi
运营到底是做什么的?
文章来源:夏叔叔(微信号:woshixiashushu),欢迎大家关注!很久没有动笔写点东西,近些日子,由于爱狗团产品上线,不断面试,经常会被问道一个问题。问:爱狗团的运营主要做什么?答:带着用户一起嗨。为什么是带着用户玩起来呢?究竟什么是运营?运营到底是做什么的?那么,我们先来回答一个更简单的问题——互联网公司对运营考核什么?以爱狗团为例,绝大部分的移动互联网公司,对运营部门的考核分为三块——用
- js面向对象类和对象
百合不是茶
js面向对象函数创建类和对象
接触js已经有几个月了,但是对js的面向对象的一些概念根本就是模糊的,js是一种面向对象的语言 但又不像java一样有class,js不是严格的面向对象语言 ,js在java web开发的地位和java不相上下 ,其中web的数据的反馈现在主流的使用json,json的语法和js的类和属性的创建相似
下面介绍一些js的类和对象的创建的技术
一:类和对
- web.xml之资源管理对象配置 resource-env-ref
bijian1013
javaweb.xmlservlet
resource-env-ref元素来指定对管理对象的servlet引用的声明,该对象与servlet环境中的资源相关联
<resource-env-ref>
<resource-env-ref-name>资源名</resource-env-ref-name>
<resource-env-ref-type>查找资源时返回的资源类
- Create a composite component with a custom namespace
sunjing
https://weblogs.java.net/blog/mriem/archive/2013/11/22/jsf-tip-45-create-composite-component-custom-namespace
When you developed a composite component the namespace you would be seeing would
- 【MongoDB学习笔记十二】Mongo副本集服务器角色之Arbiter
bit1129
mongodb
一、复本集为什么要加入Arbiter这个角色 回答这个问题,要从复本集的存活条件和Aribter服务器的特性两方面来说。 什么是Artiber? An arbiter does
not have a copy of data set and
cannot become a primary. Replica sets may have arbiters to add a
- Javascript开发笔记
白糖_
JavaScript
获取iframe内的元素
通常我们使用window.frames["frameId"].document.getElementById("divId").innerHTML这样的形式来获取iframe内的元素,这种写法在IE、safari、chrome下都是通过的,唯独在fireforx下不通过。其实jquery的contents方法提供了对if
- Web浏览器Chrome打开一段时间后,运行alert无效
bozch
Webchormealert无效
今天在开发的时候,突然间发现alert在chrome浏览器就没法弹出了,很是怪异。
试了试其他浏览器,发现都是没有问题的。
开始想以为是chorme浏览器有啥机制导致的,就开始尝试各种代码让alert出来。尝试结果是仍然没有显示出来。
这样开发的结果,如果客户在使用的时候没有提示,那会带来致命的体验。哎,没啥办法了 就关闭浏览器重启。
结果就好了,这也太怪异了。难道是cho
- 编程之美-高效地安排会议 图着色问题 贪心算法
bylijinnan
编程之美
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Random;
public class GraphColoringProblem {
/**编程之美 高效地安排会议 图着色问题 贪心算法
* 假设要用很多个教室对一组
- 机器学习相关概念和开发工具
chenbowen00
算法matlab机器学习
基本概念:
机器学习(Machine Learning, ML)是一门多领域交叉学科,涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。
它是人工智能的核心,是使计算机具有智能的根本途径,其应用遍及人工智能的各个领域,它主要使用归纳、综合而不是演绎。
开发工具
M
- [宇宙经济学]关于在太空建立永久定居点的可能性
comsci
经济
大家都知道,地球上的房地产都比较昂贵,而且土地证经常会因为新的政府的意志而变幻文本格式........
所以,在地球议会尚不具有在太空行使法律和权力的力量之前,我们外太阳系统的友好联盟可以考虑在地月系的某些引力平衡点上面,修建规模较大的定居点
- oracle 11g database control 证书错误
daizj
oracle证书错误oracle 11G 安装
oracle 11g database control 证书错误
win7 安装完oracle11后打开 Database control 后,会打开em管理页面,提示证书错误,点“继续浏览此网站”,还是会继续停留在证书错误页面
解决办法:
是 KB2661254 这个更新补丁引起的,它限制了 RSA 密钥位长度少于 1024 位的证书的使用。具体可以看微软官方公告:
- Java I/O之用FilenameFilter实现根据文件扩展名删除文件
游其是你
FilenameFilter
在Java中,你可以通过实现FilenameFilter类并重写accept(File dir, String name) 方法实现文件过滤功能。
在这个例子中,我们向你展示在“c:\\folder”路径下列出所有“.txt”格式的文件并删除。 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
- C语言数组的简单以及一维数组的简单排序算法示例,二维数组简单示例
dcj3sjt126com
carray
# include <stdio.h>
int main(void)
{
int a[5] = {1, 2, 3, 4, 5};
//a 是数组的名字 5是表示数组元素的个数,并且这五个元素分别用a[0], a[1]...a[4]
int i;
for (i=0; i<5; ++i)
printf("%d\n",
- PRIMARY, INDEX, UNIQUE 这3种是一类 PRIMARY 主键。 就是 唯一 且 不能为空。 INDEX 索引,普通的 UNIQUE 唯一索引
dcj3sjt126com
primary
PRIMARY, INDEX, UNIQUE 这3种是一类PRIMARY 主键。 就是 唯一 且 不能为空。INDEX 索引,普通的UNIQUE 唯一索引。 不允许有重复。FULLTEXT 是全文索引,用于在一篇文章中,检索文本信息的。举个例子来说,比如你在为某商场做一个会员卡的系统。这个系统有一个会员表有下列字段:会员编号 INT会员姓名
- java集合辅助类 Collections、Arrays
shuizhaosi888
CollectionsArraysHashCode
Arrays、Collections
1 )数组集合之间转换
public static <T> List<T> asList(T... a) {
return new ArrayList<>(a);
}
a)Arrays.asL
- Spring Security(10)——退出登录logout
234390216
logoutSpring Security退出登录logout-urlLogoutFilter
要实现退出登录的功能我们需要在http元素下定义logout元素,这样Spring Security将自动为我们添加用于处理退出登录的过滤器LogoutFilter到FilterChain。当我们指定了http元素的auto-config属性为true时logout定义是会自动配置的,此时我们默认退出登录的URL为“/j_spring_secu
- 透过源码学前端 之 Backbone 三 Model
逐行分析JS源代码
backbone源码分析js学习
Backbone 分析第三部分 Model
概述: Model 提供了数据存储,将数据以JSON的形式保存在 Model的 attributes里,
但重点功能在于其提供了一套功能强大,使用简单的存、取、删、改数据方法,并在不同的操作里加了相应的监听事件,
如每次修改添加里都会触发 change,这在据模型变动来修改视图时很常用,并且与collection建立了关联。
- SpringMVC源码总结(七)mvc:annotation-driven中的HttpMessageConverter
乒乓狂魔
springMVC
这一篇文章主要介绍下HttpMessageConverter整个注册过程包含自定义的HttpMessageConverter,然后对一些HttpMessageConverter进行具体介绍。
HttpMessageConverter接口介绍:
public interface HttpMessageConverter<T> {
/**
* Indicate
- 分布式基础知识和算法理论
bluky999
算法zookeeper分布式一致性哈希paxos
分布式基础知识和算法理论
BY
[email protected]
本文永久链接:http://nodex.iteye.com/blog/2103218
在大数据的背景下,不管是做存储,做搜索,做数据分析,或者做产品或服务本身,面向互联网和移动互联网用户,已经不可避免地要面对分布式环境。笔者在此收录一些分布式相关的基础知识和算法理论介绍,在完善自我知识体系的同
- Android Studio的.gitignore以及gitignore无效的解决
bell0901
androidgitignore
github上.gitignore模板合集,里面有各种.gitignore : https://github.com/github/gitignore
自己用的Android Studio下项目的.gitignore文件,对github上的android.gitignore添加了
# OSX files //mac os下 .DS_Store
- 成为高级程序员的10个步骤
tomcat_oracle
编程
What
软件工程师的职业生涯要历经以下几个阶段:初级、中级,最后才是高级。这篇文章主要是讲如何通过 10 个步骤助你成为一名高级软件工程师。
Why
得到更多的报酬!因为你的薪水会随着你水平的提高而增加
提升你的职业生涯。成为了高级软件工程师之后,就可以朝着架构师、团队负责人、CTO 等职位前进
历经更大的挑战。随着你的成长,各种影响力也会提高。
- mongdb在linux下的安装
xtuhcy
mongodblinux
一、查询linux版本号:
lsb_release -a
LSB Version: :base-4.0-amd64:base-4.0-noarch:core-4.0-amd64:core-4.0-noarch:graphics-4.0-amd64:graphics-4.0-noarch:printing-4.0-amd64:printing-4.0-noa