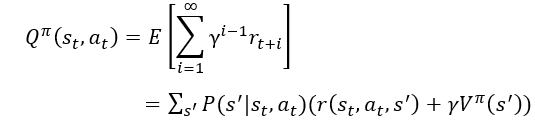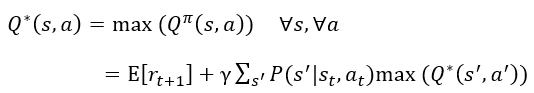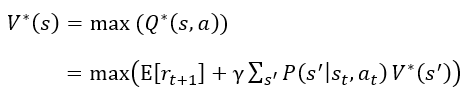深度强化学习（DRL）专栏（一）

目录：

1. 引言

• 专栏知识结构

• 从AlphaGo看深度强化学习

2. 强化学习基础知识

• 强化学习问题

• 马尔科夫决策过程

• 最优价值函数和贝尔曼方程

3. 有模型的强化学习方法

• 价值迭代

• 策略迭代

4. 无模型的强化学习方法

• 蒙特卡洛方法

• 时序差分学习

• 值函数近似

• 策略搜索

5. 实战强化学习算法

• Q-learning 算法

• Monte Carlo Policy Gradient 算法

• Actor Critic 算法

6. 深度强化学习算法

• Deep Q-Networks(DQN)

• Deep Deterministic Policy Gradient(DDPG)

7. 专栏小结

 

DeepMind团队在2013年的神经信息处理系统大会(Conference and Workshop on Neural Information Processing Systems，简称NIPS)上发表了一篇名为 “Playing Atari with Deep Reinforcement Learning”的论文，在这篇论文中，深度强化学习（Deep Reinforcement Learning）被正式提出。在论文中，DeepMind团队提出了Deep Q-Networks（DQN）算法，并且将该算法应用在了7个Atari 2600游戏中，希望让程序通过自己学习，去玩Atari游戏。其中的三个游戏，这个智能程序可以玩得比人类玩家还好！在这之后，DeepMind就被Google收购，再后来就有了那个打败李世石的AlphaGo。

 

2015年，DeepMind团队在Nature杂志上发表了一篇文章名为“Human-level control through deep reinforcement learning”的论文，在这篇论文中，他们提出了DQN算法的改进版本，他们将改进的算法应用到49种不同的Atari 2600游戏中，并且其中的一半实现了超过人类玩家的性能。现在,深度强化学习已经成为了人工智能（Artificial Intelligence，简称AI）领域最前沿的研究方向，在各个应用领域也是备受推崇，如同David Silver认为的那样，未来的人工智能一定是深度学习（Deep Learning）和强化学习（Reinforcement Learning）的结合。

 

在本专栏内容里，我们首先介绍一下强化学习的基础知识，接着介绍几种强化学习算法，并实现用强化学习算法去玩几个入门级的小游戏，最后介绍种深度强化学习算法。

 

1 引言

1.1 本专栏知识结构

近年来，强化学习的应用和研究越来越受到大家的关注，强化学习和深度学习一样，都是机器学习研究的重要分支，纵观强化学习的发展，它有着自己的一套理论和方法，尤其将深度学习和强化学习结合之后，其内容则被更加丰富了。虽然目前强化学习已经逐渐应用于人工智能、任务调度以及工业控制等领域，并展现出了其潜在的巨大应用价值，但是由于现实环境的复杂性，导致仍然有很多问题需要解决。

 

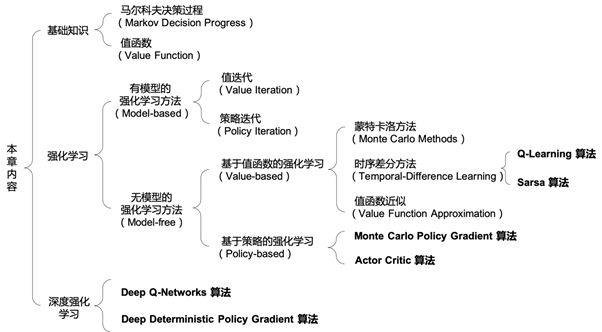
本专栏是一本实战类的书籍，所以不便花大量的篇幅去介绍强化学习的理论知识，在本专栏的前两节内容里，我们会简单的介绍一下强化学习的基础知识；在第三节和第四节内容里，我们会学习一些最基础的强化学习算法，帮助读者快速入门；第五节内容是三个强化学习算法的项目实战，通过几个小的项目帮助读者加深对算法的理解；第六节内容里会结合实战项目介绍三个深度强化学习算法，实现这三个深度强化学习算法是以前面所有内容为基础的；另外，如果读者有兴趣深入研究强化学习和深度强化学习的知识，推荐读者去学习本专栏小结里给出的推荐学习资料。本专栏主要内容结构如下：

图1 本专栏主要内容结构框架

 

1.2 从AlphaGo看深度强化学习

2016年上半年，李世石和AlphaGo（关于AlphaGo的更多信息以及最新进展，可以访问DeepMind的官方网站https://deepmind.com/）的“人机大战”掀起了一波“人工智能”的浪潮，也引起了大家对于“人工智能”的热烈讨论。虽然真正意义上的“人工智能”离我们人类还有很远，但是 AlphaGo的成功已经是一个不小的进步。在本小节的内容里，我们借助AlphaGo的例子带着读者一起粗略的了解一下，什么是深度强化学习。

 

要想搞清楚什么是深度强化学习，我们还得先了解一下什么是强化学习。一个强化学习问题通常包涵如下几个要素：

• 动作空间（Action space）：A

• 状态空间（State space）：S

• 奖励（Reward）：R

• 状态转移概率矩阵（Transition）：P

 

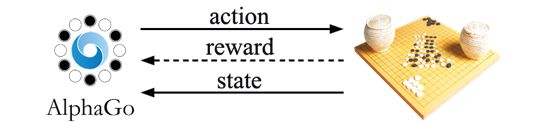
强化学习问题中有一个主体，我们称之为智能体（agent），例如AlphaGo就是一个智能主体，我们也可以认为智能主体就是指我们的计算机。动作空间（Action space）指的是智能主体可以采取的所有合法动作的集合，对AlphaGo来说，这个动作空间就是它能采取的所有合法的落子情况。对于AlphaGo来说，棋盘是它所处的环境，每一次AlphaGo落子之后（对手也随即落子），环境的状态（state）则随之发生改变，即棋盘的布局状态发生了变化，我们把所有的棋盘布局状态的集合称为状态空间（State space）。AlphaGo下完一盘棋需要采取一系列的动作，我们根据AlphaGo是否获胜来给它一个奖励（reward），如果AlphaGo获胜了，则给它一个好的奖励，告诉它这盘棋下的不错。如果AlphaGo输了，则给它一个坏的奖励，告诉它这盘棋下的不好。AlphaGo根据它最终得到的奖励，就能够知道自己在这一局棋中的一系列落子动作是好还是不好。而强化学习的目的就是让智能主体通过不断的学习，找到一个解决问题的最好的步骤序列，这个“最好”的衡量标准就是智能主体执行一系列动作后得到的累积奖励的期望。

 

图2 AlphaGo和环境（棋盘）的交互关系

 

状态转移概率矩阵（Transition）又是什么？我们知道AlphaGo每一次落子之后，对手也随即落子，这时候棋盘的状态就发生了变化，AlphaGo可以掌控自己的落子，但是却不能掌控对手的落子，对手不同的落子就会导致不同的下一个状态。事实上，AlphaGo虽然不能掌控对手的落子，但是它可以预测对手的落子情况，就像我们人类棋手一样，我们会站在对手的角度来考虑，并猜测对手的下一步棋。因此AlphaGo会预判出对手可能的落子点，给每一种情况赋予一个概率。这样就有了状态转移概率矩阵，状态转移概率矩阵会根据AlphaGo当前的动作给出所有可能的下一个棋盘状态以及对应的概率，概率最大的状态就是对手最可能的落子情况。

 

如果细想，我们会发现一个问题，我们给AlphaGo的奖励总是在它下完一盘棋之后，所以AlphaGo只知道自己这一整局棋下的怎么样，而具体到中间的每一步，则没有了评判的依据。这种情况，在强化学习问题中，我们称之为延迟奖励（Delayed reward）。要想找到一条最好的动作序列，AlphaGo就需要通过不断地学习来为每一个中间动作（或状态）赋予一个奖励，这个奖励的大小和好坏代表着这一个动作（或状态）在引领我们赢得这局棋（即获得最大累积奖励）方面表现的有多好。当AlphaGo学习到了所有中间动作（或状态）的奖励值之后，AlphaGo就可以遵循一个策略（policy），这个策略就是在每一个棋盘状态下，都执行对应奖励值最大的那一个落子动作，这就是强化学习要做的事。

 

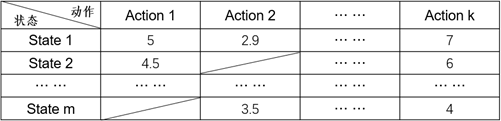
到这里，我们已经大致了解强化学习是怎么一回事了，那深度强化学习又是什么呢？前面我们说了，AlphaGo需要学习到每一个棋盘状态下可以执行的每一个动作所对应的奖励值，在一般的强化学习算法中，我们会用一张表来描述（称为Q值表），如图3所示：

 

图3 所有状态下可以执行的合法动作的奖励值

 

然而，对于围棋来说，如果是一个19×19的棋盘，摆放黑白棋子的组合数是3^361种，即使去掉那些不合法的情况，数量也依然很庞大，而且这还仅仅只是状态数，如果再算上落子动作的话，图6的那张表将会非常庞大，对于这种情况是不适合用表格来描述的，因此我们需要有个方法能够把状态的维度降低。

 

有一种可行的办法是用函数来近似表示Q值表，例如一个线性函数f(s,a,w)，其中s为状态，a为动作，w为该函数的参数，有了这个函数，只需输入一个状态以及一个合法的动作，就会知道对应的奖励是多少，而且不用关心状态s的维度有多高。考虑到通常只是状态的维度较高（例如在围棋和Atari游戏中，输入的状态都是一副图像），而动作空间往往都是低维的，我们可以将这个函数简化为f(s,w)。即只需要输入状态，输出的是形如[Q(s,a^1 ),Q(s,a^2 ),……,Q(s,a^k )]的向量，该向量包含了该状态下可以执行的所有合法的动作以及对应的奖励值。

 

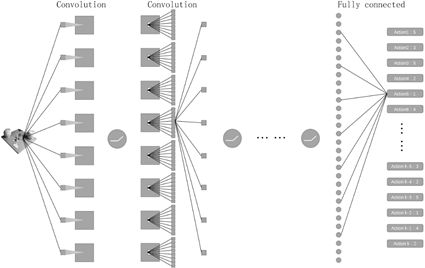
既然我们可以用一个函数来近似表示Q值表，那我们当然也可以用一个神经网络去代替这个函数，而且对于输入的状态是图像的情况，更有利于发挥神经网络的优势。我们将描述一个状态的图像输入到训练好的神经网络里，同样得到一个形如[Q(s,a^1 ),Q(s,a^2 ),……,Q(s,a^k )]的向量，我们甚至可以直接让神经网络的输出是一个确定的动作，即对应奖励值最大的那个动作，此时，智能主体就可以直接执行这个输出的动作。

 

图4 神经网络接受和处理状态图像的例子

 

2 强化学习基础知识

2.1 强化学习问题

上一节内容里，我们以AlphaGo为例简单的介绍了一下强化学习和深度强化学习，并对强化学习中的几个重要概念进行了说明。这一节内容里，我们继续学习强化学习中一些重要的基础知识。

 

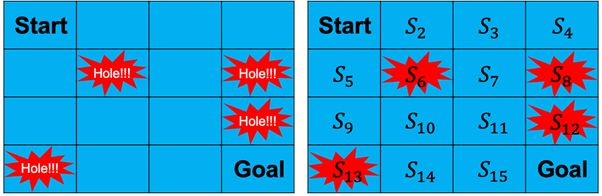
图5是一个叫做“Frozen Lake”（ “Frozen Lake”是OpenAI（https://openai.com/）的Gym工具包中的一个游戏，本专栏中我们会多次使用Gym中的小游戏作为例子，更多关于Gym工具包的信息可以访问http://gym.openai.com/docs/或https://github.com/openai/gym。）的小游戏。这个小游戏的场景是一个结了冰的湖面（如图所示，为一个4X4大小的方格），游戏要求我们的agent从开始点“Start”走到目标点“Goal”，但是不能掉进冰窟窿里（图中标注的“Hole”）。这个小游戏有两种模式：“有风”模式和“无风”模式。两种模式的区别是，在“有风”模式下，agent的移动会受到风的影响。例如，agent当前的位置是S_3，agent选择向右走一步，“无风”模式下agent会到达S_4状态，而在“有风”模式下，agent的位置则不确定了，有可能会被风吹到其它状态，例如S_7。

 

图5 “Frozen Lake”游戏示意图

 

在我们看来，“Frozen Lake”是一个非常简单的游戏，但是对于我们的agent来说它并不知道自己所处的环境是什么样子，也不知道要怎么去玩这个游戏。他只能通过和环境交互，即不断地尝试每一种动作，然后根据环境的反馈来判断刚才的动作是好还是不好。例如agent当前处在S_5状态，它采取了一个向右的动作，结果掉进了冰窟窿，此时环境会给它一个负的反馈，告诉它刚才这个动作是不好的。而如果agent是处在S_15状态，它采取了一个向右的动作，环境则会给它一个正的反馈，因为它顺利到达了目标点。

 

正如我们在第一节内容里介绍的，agent需要通过学习，然后得到每一个中间动作（或状态）的奖励值，之后的策略就是选择一条累积奖励最大的动作序列（即每一次都选择当前状态下奖励值最大的那个动作执行）。后面的内容里，我们会介绍agent是如何通过学习得到每一个中间动作（或状态）的奖励值。

 

1. 累积奖励

在“Frozen Lake”游戏中，agent从开始点移动到目标点需要经过一个序列的中间状态，同时也需要根据策略做出一系列的动作。对于这个策略优劣的评价，我们通常根据agent执行完一个序列的动作后所获得的累积奖励来评判，累积得到的奖励越大，则认为策略越优。

 

对于计算累积奖励有两种方式，一种是计算从当前状态到结束状态的所有奖励之和：

式1

式1适用于有限时界（finite-horizon）情况下的强化学习，但是考虑到有些无限时界（finite-horizon）情况，agent要执行的可能是一个时间持续很长的任务，比如自动驾驶，在这种情况下如果使用上式计算累积奖励显然是不合理的，我们需要一个有限的值，所以通常我们会增加一个折扣因子，如下式：

 

 式2

在上式中，0≤γ≤1。当γ的值等于0时，则agent只考虑下一步的回报，当γ的值越趋近于1，未来的奖励就会被更多的考虑在内，需要注意的是，有时候我们会更关心眼下的奖励，有时候则会更关心未来的奖励，调整的方式就是修改γ的值。

 

2. 学习（Learning）和规划（Planning）

学习（Learning）问题不同于规划（Planning）问题，规划问题一般只需求得一个解，或者是找寻一条路径，而学习问题是要求得一个策略（或者说是对一个问题的解决方法的建模），agent使用这个策略去采取一系列的动作并完成任务，例如在“Frozen Lake”游戏中从开始位置“Start”走到目标位置“Goal”。

 

在规划问题中我们有着关于这个问题的完整描述，例如求最短路径问题，我们知道图中所有的节点和所有的边，以及每一条边上的权重。而在学习问题中，我们对问题往往没有一个完整的描述，例如在“Frozen Lake”游戏中，agent对环境并不清楚，初始情况下，对于每一个动作（或状态）也没有一个固定的奖励，agent只有在掉进冰窟窿或者是到达目标点的时候才会得到一个相应的奖励。而且如果是在“有风”的模式下，我们甚至连执行一个动作后会到达的下一个状态都不确定。

 

虽然说学习问题不同于规划问题，但是两者也有一定的联系。在后面的内容里，我们会介绍一类基于模型（model-based）的强化学习方法，在这类方法所适用的场景中，拥有关于环境的完整的描述（例如所有的环境状态、状态转移概率矩阵以及关于动作（或状态）的奖励等）。基于模型（model-based）的强化学习方法会先从环境中恢复这些环境信息，并保存在一个模型中（即我们后面会介绍的马尔科夫决策过程）。在得到这个模型之后，我们就可以使用规划的方法来解决问题了。与之对应的还有一类称为无模型的（model-free）强化学习方法，这类方法不需要知道完整的环境信息，也不会对环境建模，而是通过直接和环境交互来进行学习。

 

强化学习也不同于传统的有监督学习，关于两者的区别，埃塞姆·阿培丁（Ethem Alpaydin）教授在其所著的《Introduction to Machine Learning》一书中提到：有监督学习是“learning with a teacher”，而强化学习是“learning with a critic”。批评者（critic）不会告诉我们做什么，他只会在事后告诉我们做得怎么样（例如在“Frozen Lake”游戏中，只有在agent掉进冰窟窿或者到达目标位置后，才会得到一个反馈信息，而这时游戏已经结束了）。所以我们需要根据批评者事后的评价去回头评估和调整我们之前的动作，直到能得到批评者最好的评价。

2.2 马尔科夫决策过程

一个马尔科夫决策过程（Markov Decision Processes，MDP）是对强化学习中环境（Environment）的形式化的描述，或者说是对于agent所处的环境的一个建模。在强化学习中，几乎所有的问题都可以形式化的表示为一个MDP。

 

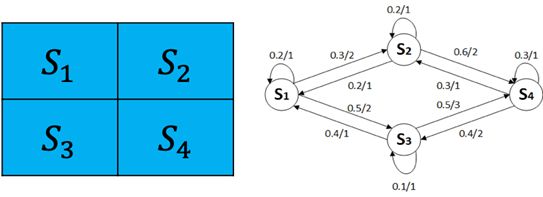
我们将“Frozen Lake”（无风模式）简化一下，并且我们不考虑起点和终点，如图6：

 

     

图6 简化的“Frozen Lake”游戏

 

图6中右侧的状态转换图，表示从每个状态转移到下一个状态的概率以及能获得的相应奖励。

 

例如在状态S_1时，可以转移到S_2状态，也可以转移到S_3状态，或者不移动留在S_1状态。其概率分别为0.3、0.5和0.2，获得的相应奖励分别为2、2和1。对于每一个状态来说，出边的概率和必为1。

 

1. 马尔科夫过程（Markov Process）

在一个随机过程s_0,s_1,…,s_n中，已知时刻t_i所处的状态s_i，如果在时刻t_(i+1)时的状态s_(i+1)只与状态s_i相关，而与t_i时刻之前的状态无关，则称这个过程为马尔科夫过程。例如图10-6中的例子，agent从S_1状态移动到S_3状态后，至于下一个状态是什么已经与S_1无关了，只取决于当前的S_3状态。这种特性称为随机过程的马尔科夫性（或称为“无后效性”）。具有马尔科夫性质的随机过程s_0,s_1,…,s_n称为马尔科夫链（Markov Chain）。

 

2. 马尔科夫回报过程（Markov Reward Process）

在2.1节中，我们在讨论计算累积奖励的时候给出了公式1和2。这两个公式考虑的是最简单的情况（即agent每执行一个动作后，到达的下一个状态是确定的），所以仅需要将agent每一步获得的奖励累加起来。然而，很多时候环境的状态是不确定的，例如在“Frozen Lake”游戏的“有风”模式下，agent执行一个动作后会以一定的概率转移到另一个状态，因此得到的奖励也与这个概率相关。所以在计算累积奖励的时候，通常是计算奖励的期望，我们用V表示奖励的期望，则状态s的期望奖励值表示为：

式3

所以公式1可表示为如下形式：

 

式4

公式2（考虑折扣因子）则表示为：

式5

 

3. 马尔科夫决策过程（Markov Decision Process）

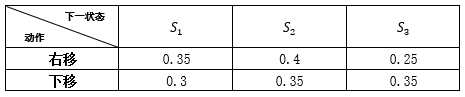
在图6的例子中我们只考虑了“Frozen Lake”游戏的“无风”模式，因为在“无风”模式下，agent执行了一个动作后就会确定的到达下一个状态，所以我们只考虑了状态的转移而无需考虑到具体的动作。然而在“有风”模式下，根据执行的动作不同，状态的转移概率也不同。依然以图6中简化后的“Frozen Lake”游戏例子，假如我们当前状态为S_1，在“有风”的情况下，根据我们执行的动作不同，状态转移概率如下表所示：

 

表1 “有风”模式下agent在S_1状态时执行不同动作的状态转移概率

 

什么是马尔科夫决策过程？我们将马尔科夫决策过程定义为一个五元组：

式6

• S ：状态空间（State space），例如在“Frozen Lake”游戏中，总共有16个状态（Start，S_2，…，S_15，Goal）；

• A ：动作空间（Action space），在“Frozen Lake”游戏中，每个状态下可以执行的动作有四个（上、下、左、右）；

• R ：S×A→R，奖励函数（Reward function），在某个状态S_t下我们执行了一个动作并转移到下一个状态S_(t+1)，就会得到一个相应的奖励r_(t+1)；

• P ：S×A→S，状态转移规则（Transition），可以理解为我们之前介绍的状态转移概率矩阵。在某个状态S_t下我们执行了一个动作，就会以一定的概率转移到下一个状态S_(t+1)。

   

现在我们总结一下，强化学习要解决的问题是：agent需要学习一个策略（policy）π，这个策略π定义了从状态到动作的一个映射关系π:S→A,也就是说，agent在任意状态s_t下所能执行的动作为：a_t=π(s_t)，并且有

我们用价值V^π来衡量这个策略π的好坏，价值V^π (s_t)代表的是agent从状态s_t开始，在遵循策略π的前提下执行一系列动作后获得的累积奖励的期望值（事实上，当策略π确定后，那么MDP中的状态转移概率也就确定了，此时可以简单的看作是马尔科夫回报过程，求解回报的方式就可以使用求解马尔科夫回报过程的方式）：

 

式7

与公式5不同的是，这里的价值是在遵循策略π的情况下的价值。

2.3 最优价值函数和贝尔曼方程

公式7称为价值函数（value function），他可以用来表明在遵循策略π的前提下当前状态的价值。在强化学习中，我们想要找到一个最优的策略（optimal policy）π^*，使得在任意初始状态s下，能够最大化价值函数，称为最优价值函数（optimal value function）：

式8

在强化学习问题中，很多时候，我们想要知道的是在每个状态上做哪个动作最好，然而最优价值函数只能告诉我们当前状态的价值是多少，agent只能每个动作尝试一下，走到下一个状态，看哪个动作导致的下一个状态的价值是最好的，就用哪一个动作。

 

为了避免麻烦，我们常用动作价值函数（又称Q值函数）。Q值函数比V函数多了一个动作输入，它要估计的是在状态s下执行了动作a以后，再跟着这个策略π一直走下去，它的累积奖励是多少。有了Q值函数，看到状态s后，把每个动作a带进去，看执行哪个动作a得到的Q值最大，就用哪个动作a。

 

所以我们处理成对的状态-动作的价值Q(s_t,a_t)。Q(s_t,a_t)表示当处于状态s_t时执行动作a_t的价值。

                                         

式9

因此，最优动作价值函数为：

式10

所以状态的价值就等于在这个状态上可以采取的最优动作的价值，即：

式11

得到Q^* (s,a)值后，我们就可以定义策略π为执行动作a^*，它在所有的Q^* (s,a)中具有最大值，即：

 

所以，只要获得所有的Q^* (s,a)值，那么在每个局部步骤中使用贪心搜素，就可以得到一个最优的步骤序列，该序列最大化累积奖励。

 

形如的方程称之为贝尔曼方程。和满足贝尔曼方程，公式10和11称为贝尔曼最优方程（Bellman optimality equation），有了贝尔曼方程和贝尔曼最优方程，我们就可以使用动态规划的方法来求解MDP。

 

 

欢迎关注磐创博客资源汇总站：
http://docs.panchuang.net/

欢迎关注PyTorch官方中文教程站：
http://pytorch.panchuang.net/