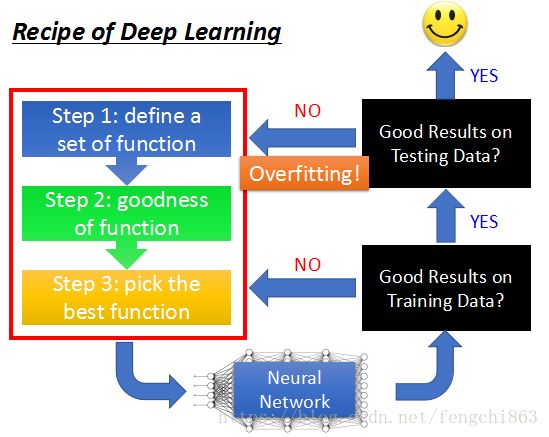
梯度弥散与梯度爆炸
问题描述
先来看看问题描述。
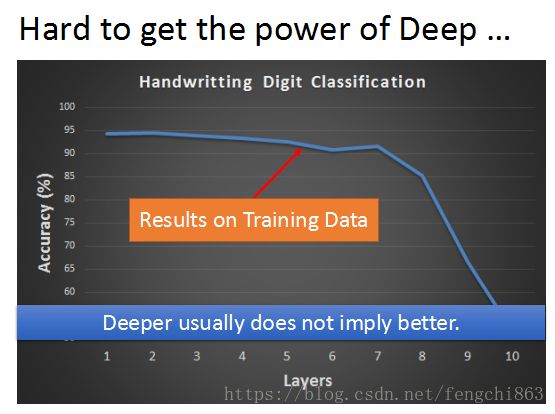
当我们使用sigmoid funciton 作为激活函数时,随着神经网络hidden layer层数的增加,训练误差反而加大了,如上图所示。
下面以2层隐藏层神经网络为例,进行说明。
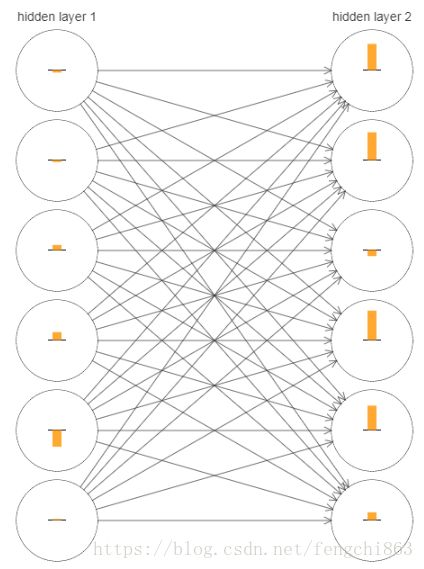
结点中的柱状图表示每个神经元参数的更新速率(梯度)大小,有图中可以看出,layer2整体速度都要大于layer1.
我们又取每层layer中参数向量的长度来粗略的估计该层的更新速率,得到下图。
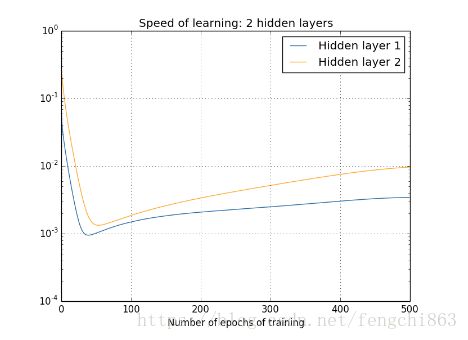
可以看出,layer2的速率都要大于layer1.
然后我们继续加深神经网络的层数。
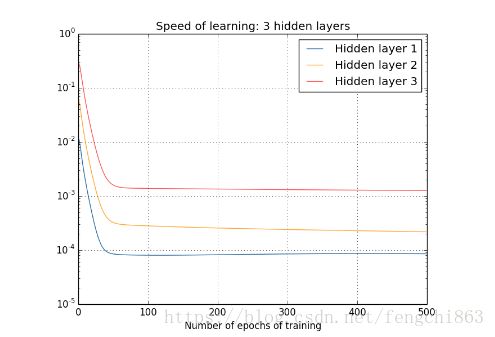
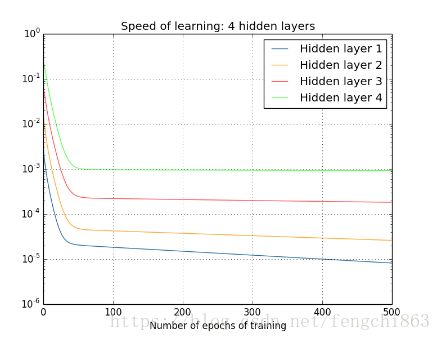
可以得到下面的结论:
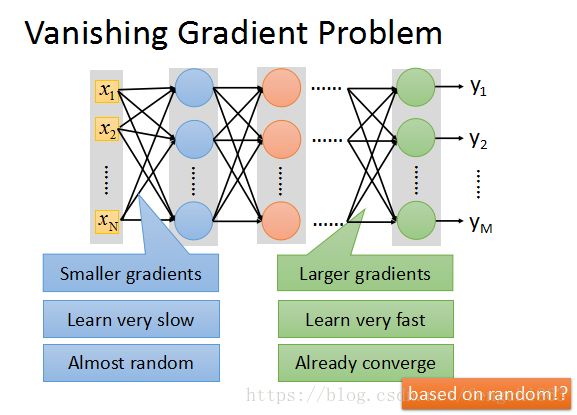
靠近输出层的hidden layer 梯度大,参数更新快,所以很快就会收敛;
而靠近输入层的hidden layer 梯度小,参数更新慢,几乎就和初始状态一样,随机分布。
在上面的四层隐藏层网络结构中,第一层比第四层慢了接近100倍!!
这种现象就是梯度弥散(vanishing gradient problem)。而在另一种情况中,前面layer的梯度通过训练变大,而后面layer的梯度指数级增大,这种现象又叫做梯度爆炸(exploding gradient problem)。
总的来说,就是在这个深度网络中,梯度相当不稳定(unstable)。
直观说明
那么为何会出现这种情况呢?
现在我们来直观的说明一下。

在上面的升级网络中,我们随意更新一个参数,加上一个Δw,(我们知道可以使用参数变化量来估计偏导数的大小)这个参数的更新会随着网络向前传播。
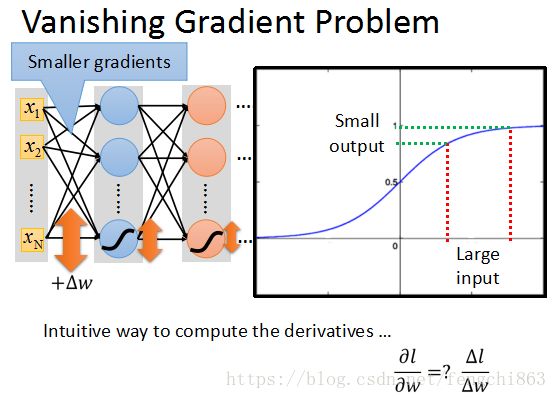
而根据sigmoid的特点,它会将负无穷到正无穷之间的输入压缩到0~1之间。当input的值更新时,output会有很小的更新。
又因为上一层的输出将作为后一层的输入,而输出经过sigmoid后更新速率会逐步衰减,直到输出层只会有微乎其微的更新。
数学说明
为了弄清楚为何会出现消失的梯度,来看看一个极简单的深度神经网络:每一层都只有一个单一的神经元。下面就是有三层隐藏层的神经网络:

我们把梯度的整个表达式写出来:

为了理解每个项的行为,先看下sigmoid函数导数的曲线:

该导数在 σ′(0)=14 σ ′ ( 0 ) = 1 4 时达到最高。现在,如果我们使用标准方法来初始化网络中的权重,那么会使用 一个均值为0标准差为1的高斯分布(也就是正态分布)。因此所有的权重通常会满足 |wj|<1 | w j | < 1 。有了这些信息,我们发现会有 wjσ′(zj)<14 w j σ ′ ( z j ) < 1 4 ,并且在进行所有这些项的乘积时,最终结果肯定会指数级下降:项越多,乘积的下降也就越快。
下面我们从公式上比较一下第三层和第一层神经元的学习速率:

比较一下 ∂C∂b1 ∂ C ∂ b 1 和 ∂C∂b3 ∂ C ∂ b 3 可知, ∂C∂b1 ∂ C ∂ b 1 要远远小于 ∂C∂b3 ∂ C ∂ b 3 。因此,梯度消失的本质原因是: wjσ′(zj)<14 w j σ ′ ( z j ) < 1 4 的约束。
梯度激增问题
举个例子说明下:
首先,我们将网络的权重设置得很大,比如 w1=w2=w3=w4=100 w 1 = w 2 = w 3 = w 4 = 100 ,然后,我们选择偏置使得 σ′(zj) σ ′ ( z j ) 项不会太小。这是很容易实现的:方法就是选择偏置来保证每个神经元的带权输入是 zj=0 z j = 0 (这样 wjσ′(zj)=14 w j σ ′ ( z j ) = 1 4 )。比如说,我们希望 z1=w1∗a0+b1 z 1 = w 1 ∗ a 0 + b 1 ,我们只需要把 b1=−100∗a0 b 1 = − 100 ∗ a 0 即可。我们使用相同的方法来获取其他的偏置。这样我们可以发现所有的项 wj∗σ′(zj) w j ∗ σ ′ ( z j ) ,都等于 100∗1/4=25 100 ∗ 1 / 4 = 25 。最终,我们获得了激增的梯度。
梯度爆炸的原因:在train的时候如果参数w变得足够大,就可能使 |w|>1 | w | > 1 ,那样 wjσ′(zj)<14 w j σ ′ ( z j ) < 1 4 就不满足了,的确这样不会有梯度弥散问题,根据我们之前的分析,当 |w|>1 | w | > 1 时,会使后面的layer参数指数级增加,从而引发梯度爆炸。
不稳定的梯度问题:根本的问题其实并非是消失的梯度问题或者激增的梯度问题,而是在前面的层上的梯度是来自后面的层上项的乘积。当存在过多的层次时,就出现了内在本质上的不稳定场景。唯一让所有层都接近相同的学习速度的方式是所有这些项的乘积都能得到一种平衡。如果没有某种机制或者更加本质的保证来达成平衡,那网络就很容易不稳定了。简而言之,真实的问题就是神经网络受限于不稳定梯度的问题。所以,如果我们使用标准的基于梯度的学习算法,在网络中的不同层会出现按照不同学习速度学习的情况。
解决方法
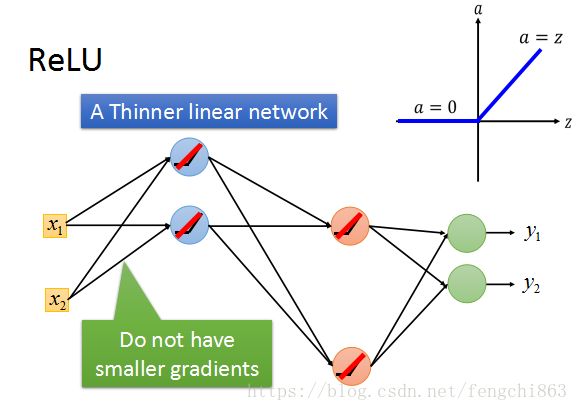
梯度不稳定的方法就是,使用其他激活函数替代sigmoid,比如Relu等等,这里就不细说了。


参考文献:
[1] Why are deep neural networks hard to train?
[2] 梯度弥散与梯度爆炸
[3] 深度学习中消失的梯度