【转】隐马尔科夫模型(HMM)及其Python实现
原文链接https://applenob.github.io/hmm.html
隐马尔科夫模型(HMM)及其Python实现
目录
- 1.基础介绍
- 形式定义
- 隐马尔科夫模型的两个基本假设
- 一个关于感冒的实例
- 2.HMM的三个问题
- 2.1概率计算问题
- 2.2学习问题
- 2.3预测问题
- 3.完整代码
1.基础介绍
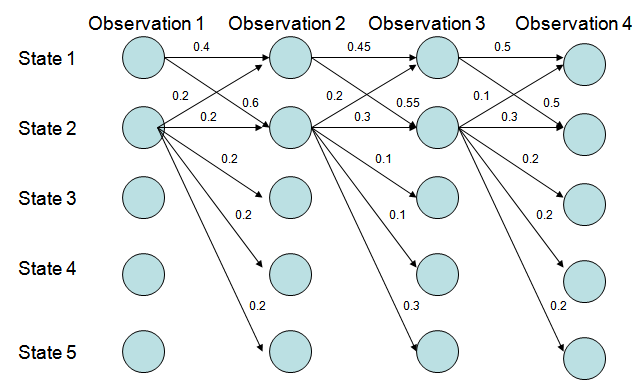
描述下这个图:
分成两排,第一排是yy序列,第二排是xx序列。每个xx都只有一个yy指向它,每个yy也都有另一个yy指向它。
OK,直觉上的东西说完了,下面给出定义(参考《统计学习方法》):
- 状态序列(上图中的yy,下面的II): 隐藏的马尔科夫链随机生成的状态序列,称为状态序列(state sequence)
- 观测序列(上图中的xx,下面的OO): 每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列(obeservation sequence)
- 马尔科夫模型: 马尔科夫模型是关于时序的概率模型,描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。
形式定义
设QQ是所有可能的状态的集合,VV是所有可能的观测的集合。
Q=q1,q2,...,qN,V=v1,v2,...,vMQ=q1,q2,...,qN,V=v1,v2,...,vM
其中,NN是可能的状态数,MM是可能的观测数。
II是长度为TT的状态序列,OO是对应的观测序列。
I=(i1,i2,...,iT),O=(o1,o2,...,oT)I=(i1,i2,...,iT),O=(o1,o2,...,oT)
A是状态转移矩阵:A=[aij]N×NA=[aij]N×N
i=1,2,...,N;j=1,2,...,Ni=1,2,...,N;j=1,2,...,N
其中,在时刻tt,处于qiqi 状态的条件下在时刻t+1t+1转移到状态qjqj 的概率:
aij=P(it+1=qj|it=qi)aij=P(it+1=qj|it=qi)
B是观测概率矩阵:B=[bj(k)]N×MB=[bj(k)]N×M
k=1,2,...,M;j=1,2,...,Nk=1,2,...,M;j=1,2,...,N
其中,在时刻tt处于状态qjqj 的条件下生成观测vkvk 的概率:
bj(k)=P(ot=vk|it=qj)bj(k)=P(ot=vk|it=qj)
π是初始状态概率向量:π=(πi)π=(πi)
其中,πi=P(i1=qi)πi=P(i1=qi)
隐马尔科夫模型由初始状态概率向量ππ、状态转移概率矩阵A和观测概率矩阵BB决定。ππ和AA决定状态序列,BB决定观测序列。因此,隐马尔科夫模型λλ可以由三元符号表示,即:λ=(A,B,π)λ=(A,B,π)。A,B,πA,B,π称为隐马尔科夫模型的三要素。
隐马尔科夫模型的两个基本假设
(1):设隐马尔科夫链在任意时刻tt的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻tt无关。(齐次马尔科夫性假设)
(2):假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测和状态无关。(观测独立性假设)
一个关于感冒的实例
定义讲完了,举个实例,参考hankcs和知乎上的感冒预测的例子(实际上都是来自wikipidia:https://en.wikipedia.org/wiki/Viterbi_algorithm#Example ),这里我用最简单的语言去描述。
假设你是一个医生,眼前有个病人,你的任务是确定他是否得了感冒。
- 首先,病人的状态(QQ)只有两种:{感冒,没有感冒}。
- 然后,病人的感觉(观测VV)有三种:{正常,冷,头晕}。
- 手头有病人的病例,你可以从病例的第一天确定ππ(初始状态概率向量);
- 然后根据其他病例信息,确定AA(状态转移矩阵)也就是病人某天是否感冒和他第二天是否感冒的关系;
- 还可以确定BB(观测概率矩阵)也就是病人某天是什么感觉和他那天是否感冒的关系。
In [1]:
import numpy as np
In [2]:
# 对应状态集合Q
states = ('Healthy', 'Fever')
# 对应观测集合V
observations = ('normal', 'cold', 'dizzy')
# 初始状态概率向量π
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
# 状态转移矩阵A
transition_probability = {
'Healthy': {'Healthy': 0.7, 'Fever': 0.3},
'Fever': {'Healthy': 0.4, 'Fever': 0.6},
}
# 观测概率矩阵B
emission_probability = {
'Healthy': {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
'Fever': {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6},
}
In [3]:
# 随机生成观测序列和状态序列
def simulate(T):
def draw_from(probs):
"""
1.np.random.multinomial:
按照多项式分布,生成数据
>>> np.random.multinomial(20, [1/6.]*6, size=2)
array([[3, 4, 3, 3, 4, 3],
[2, 4, 3, 4, 0, 7]])
For the first run, we threw 3 times 1, 4 times 2, etc.
For the second, we threw 2 times 1, 4 times 2, etc.
2.np.where:
>>> x = np.arange(9.).reshape(3, 3)
>>> np.where( x > 5 )
(array([2, 2, 2]), array([0, 1, 2]))
"""
return np.where(np.random.multinomial(1,probs) == 1)[0][0]
observations = np.zeros(T, dtype=int)
states = np.zeros(T, dtype=int)
states[0] = draw_from(pi)
observations[0] = draw_from(B[states[0],:])
for t in range(1, T):
states[t] = draw_from(A[states[t-1],:])
observations[t] = draw_from(B[states[t],:])
return observations, states
In [4]:
def generate_index_map(lables):
id2label = {}
label2id = {}
i = 0
for l in lables:
id2label[i] = l
label2id[l] = i
i += 1
return id2label, label2id
states_id2label, states_label2id = generate_index_map(states)
observations_id2label, observations_label2id = generate_index_map(observations)
print(states_id2label, states_label2id)
print(observations_id2label, observations_label2id)
{0: 'Healthy', 1: 'Fever'} {'Healthy': 0, 'Fever': 1}
{0: 'normal', 1: 'cold', 2: 'dizzy'} {'normal': 0, 'cold': 1, 'dizzy': 2}
In [5]:
def convert_map_to_vector(map_, label2id):
"""将概率向量从dict转换成一维array"""
v = np.zeros(len(map_), dtype=float)
for e in map_:
v[label2id[e]] = map_[e]
return v
def convert_map_to_matrix(map_, label2id1, label2id2):
"""将概率转移矩阵从dict转换成矩阵"""
m = np.zeros((len(label2id1), len(label2id2)), dtype=float)
for line in map_:
for col in map_[line]:
m[label2id1[line]][label2id2[col]] = map_[line][col]
return m
In [6]:
A = convert_map_to_matrix(transition_probability, states_label2id, states_label2id) print(A) B = convert_map_to_matrix(emission_probability, states_label2id, observations_label2id) print(B) observations_index = [observations_label2id[o] for o in observations] pi = convert_map_to_vector(start_probability, states_label2id) print(pi)
[[ 0.7 0.3] [ 0.4 0.6]] [[ 0.5 0.4 0.1] [ 0.1 0.3 0.6]] [ 0.6 0.4]
In [7]:
# 生成模拟数据
observations_data, states_data = simulate(10)
print(observations_data)
print(states_data)
# 相应的label
print("病人的状态: ", [states_id2label[index] for index in states_data])
print("病人的观测: ", [observations_id2label[index] for index in observations_data])
[0 0 1 1 2 1 2 2 2 0] [0 0 0 0 1 1 1 1 1 0] 病人的状态: ['Healthy', 'Healthy', 'Healthy', 'Healthy', 'Fever', 'Fever', 'Fever', 'Fever', 'Fever', 'Healthy'] 病人的观测: ['normal', 'normal', 'cold', 'cold', 'dizzy', 'cold', 'dizzy', 'dizzy', 'dizzy', 'normal']
2.HMM的三个问题
HMM在实际应用中,一般会遇上三种问题:
- 1.概率计算问题:给定模型λ=(A,B,π)λ=(A,B,π) 和观测序列O=o1,o2,...,oTO=o1,o2,...,oT,计算在模型λλ下观测序列OO出现的概率P(O|λ)P(O|λ)。
- 2.学习问题:已知观测序列O=o1,o2,...,oTO=o1,o2,...,oT,估计模型λ=(A,B,π)λ=(A,B,π),使P(O|λ)P(O|λ)最大。即用极大似然法的方法估计参数。
- 3.预测问题(也称为解码(decoding)问题):已知观测序列O=o1,o2,...,oTO=o1,o2,...,oT 和模型λ=(A,B,π)λ=(A,B,π),求给定观测序列条件概率P(I|O)P(I|O)最大的状态序列I=(i1,i2,...,iT)I=(i1,i2,...,iT),即给定观测序列,求最有可能的对应的状态序列。
回到刚才的例子,这三个问题就是:
- 1.概率计算问题:如果给定模型参数,病人某一系列观测的症状出现的概率。
- 2.学习问题:根据病人某一些列观测的症状,学习模型参数。
- 3.预测问题:根据学到的模型,预测病人这几天是不是有感冒。
2.1 概率计算问题
概率计算问题计算的是:在模型λλ下观测序列OO出现的概率P(O|λ)P(O|λ)。
直接计算:
对于状态序列I=(i1,i2,...,iT)I=(i1,i2,...,iT)的概率是:P(I|λ)=πi1ai1i2ai2i3...aiT−1iTP(I|λ)=πi1ai1i2ai2i3...aiT−1iT。
对上面这种状态序列,产生观测序列O=(o1,o2,...,oT)O=(o1,o2,...,oT)的概率是P(O|I,λ)=bi1(o1)bi2(o2)...biT(oT)P(O|I,λ)=bi1(o1)bi2(o2)...biT(oT)。
II和OO的联合概率为P(O,I|λ)=P(O|I,λ)P(I|λ)=πi1bi1(o1)ai1i2bi2(o2)...aiT−1iTbiT(oT)P(O,I|λ)=P(O|I,λ)P(I|λ)=πi1bi1(o1)ai1i2bi2(o2)...aiT−1iTbiT(oT)。
对所有可能的II求和,得到P(O|λ)=∑IP(O,I|λ)=∑i1,...,iTπi1bi1(o1)ai1i2bi2(o2)...aiT−1iTbiT(oT)P(O|λ)=∑IP(O,I|λ)=∑i1,...,iTπi1bi1(o1)ai1i2bi2(o2)...aiT−1iTbiT(oT)。
如果直接计算,时间复杂度太高,是O(TNT)O(TNT)。
前向算法(或者后向算法):
首先引入前向概率:
给定模型λλ,定义到时刻tt部分观测序列为o1,o2,...,oto1,o2,...,ot 且状态为qiqi 的概率为前向概率。记作:
αt(i)=P(o1,o2,...,ot,it=qi|λ)αt(i)=P(o1,o2,...,ot,it=qi|λ)
用感冒例子描述就是:某一天是否感冒以及这天和这天之前所有的观测症状的联合概率。
后向概率定义类似。
前向算法
输入:隐马模型λλ,观测序列OO; 输出:观测序列概率P(O|λ)P(O|λ).
-
- 初值(t=1)(t=1),α1(i)=P(o1,i1=q1|λ)=πibi(o1)α1(i)=P(o1,i1=q1|λ)=πibi(o1),i=1,2,...,Ni=1,2,...,N
-
- 递推:对t=1,2,...,Nt=1,2,...,N,αt+1(i)=[∑Nj=1αt(j)aji]bi(ot+1)αt+1(i)=[∑j=1Nαt(j)aji]bi(ot+1)
-
- 终结:P(O|λ)=∑Ni=1αT(i)P(O|λ)=∑i=1NαT(i)
前向算法理解:
前向算法使用前向概率的概念,记录每个时间下的前向概率,使得在递推计算下一个前向概率时,只需要上一个时间点的所有前向概率即可。原理上也是用空间换时间。这样的时间复杂度是O(N2T)O(N2T)。
前向算法/后向算法python实现:
In [8]:
def forward(obs_seq):
"""前向算法"""
N = A.shape[0]
T = len(obs_seq)
# F保存前向概率矩阵
F = np.zeros((N,T))
F[:,0] = pi * B[:, obs_seq[0]]
for t in range(1, T):
for n in range(N):
F[n,t] = np.dot(F[:,t-1], (A[:,n])) * B[n, obs_seq[t]]
return F
def backward(obs_seq):
"""后向算法"""
N = A.shape[0]
T = len(obs_seq)
# X保存后向概率矩阵
X = np.zeros((N,T))
X[:,-1:] = 1
for t in reversed(range(T-1)):
for n in range(N):
X[n,t] = np.sum(X[:,t+1] * A[n,:] * B[:, obs_seq[t+1]])
return X
2.2学习问题
学习问题我们这里只关注非监督的学习算法,有监督的学习算法在有标注数据的前提下,使用极大似然估计法可以很方便地估计模型参数。
非监督的情况,也就是我们只有一堆观测数据,对应到感冒预测的例子,即,我们只知道病人之前的几天是什么感受,但是不知道他之前是否被确认为感冒。
在这种情况下,我们可以使用EM算法,将状态变量视作隐变量。使用EM算法学习HMM参数的算法称为Baum-Weich算法。
模型表达式:
P(O|λ)=∑IP(O|I,λ)P(I|λ)P(O|λ)=∑IP(O|I,λ)P(I|λ)
Baum-Weich算法:
(1). 确定完全数据的对数似然函数
完全数据是(O,I)=(o1,o2,...,oT,i1,...,iT)(O,I)=(o1,o2,...,oT,i1,...,iT)
完全数据的对数似然函数是:logP(O,I|λ)logP(O,I|λ)。
(2). EM算法的E步:
Q(λ,λ^)=∑IlogP(O,I|λ)P(O,I|λ^)Q(λ,λ^)=∑IlogP(O,I|λ)P(O,I|λ^)
注意,这里忽略了对于λλ而言是常数因子的1P(O|λ^)1P(O|λ^)
其中,λ^λ^ 是隐马尔科夫模型参数的当前估计值,λ是要极大化的因马尔科夫模型参数。
又有:
P(O,I|λ)=πi1bi1(o1)ai1,i2bi2(o2)...aiT−1,iTbiT(oT)P(O,I|λ)=πi1bi1(o1)ai1,i2bi2(o2)...aiT−1,iTbiT(oT)
于是Q(λ,λ^)Q(λ,λ^)可以写成:
Q(λ,λ^)=∑Ilogπi1P(O,I|λ^)+∑I(∑t=1T−1logait−1,it)P(O,I|λ^)+∑I(∑t=1T−1logbit(ot))P(O,I|λ^)Q(λ,λ^)=∑Ilogπi1P(O,I|λ^)+∑I(∑t=1T−1logait−1,it)P(O,I|λ^)+∑I(∑t=1T−1logbit(ot))P(O,I|λ^)
(3). EM算法的M步:
极大化Q函数Q(λ,λ^)Q(λ,λ^) 求模型参数A,B,πA,B,π。
应用拉格朗日乘子法对各参数求偏导,解得Baum-Weich模型参数估计公式:
- aij=∑T−1t=1ξt(i,j)∑T−1t=1γt(i)aij=∑t=1T−1ξt(i,j)∑t=1T−1γt(i)
- bj(k)=∑Tt=1,ot=vkγt(j)∑Tt=1γt(j)bj(k)=∑t=1,ot=vkTγt(j)∑t=1Tγt(j)
- πi=γ1(i)πi=γ1(i)
其中γt(i)γt(i)和ξt(i,j)ξt(i,j)是:
γt(i)=P(it=qi|O,λ)=P(it=qi,O|λ)P(O|λ)=αt(i)βt(i)∑Nj=1αt(j)βt(j)γt(i)=P(it=qi|O,λ)=P(it=qi,O|λ)P(O|λ)=αt(i)βt(i)∑j=1Nαt(j)βt(j)
读作gamma,即,给定模型参数和所有观测,时刻tt处于状态qiqi的概率。
ξt(i,j)=P(it=qi,ii+1=qj|O,λ)=P(it=qi,ii+1=qj,O|λ)P(O|λ)=P(it=qi,ii+1=qj,O|λ)∑Ni=1∑Nj=1P(it=qi,ii+1=qj,O|λ)ξt(i,j)=P(it=qi,ii+1=qj|O,λ)=P(it=qi,ii+1=qj,O|λ)P(O|λ)=P(it=qi,ii+1=qj,O|λ)∑i=1N∑j=1NP(it=qi,ii+1=qj,O|λ)
读作xi,即,给定模型参数和所有观测,时刻tt处于状态qiqi且时刻t+1t+1处于状态qjqj的概率。
带入P(it=qi,ii+1=qj,O|λ)=αt(i)aijbj(ot+1)βt+1(j)P(it=qi,ii+1=qj,O|λ)=αt(i)aijbj(ot+1)βt+1(j)
得到:ξt(i,j)=αt(i)aijbj(ot+1)βt+1(j)∑Ni=1∑Nj=1αt(i)aijbj(ot+1)βt+1(j)ξt(i,j)=αt(i)aijbj(ot+1)βt+1(j)∑i=1N∑j=1Nαt(i)aijbj(ot+1)βt+1(j)
Baum-Weich算法的python实现:
In [9]:
def baum_welch_train(observations, A, B, pi, criterion=0.05):
"""无监督学习算法——Baum-Weich算法"""
n_states = A.shape[0]
n_samples = len(observations)
done = False
while not done:
# alpha_t(i) = P(O_1 O_2 ... O_t, q_t = S_i | hmm)
# Initialize alpha
alpha = forward(observations)
# beta_t(i) = P(O_t+1 O_t+2 ... O_T | q_t = S_i , hmm)
# Initialize beta
beta = backward(observations)
# ξ_t(i,j)=P(i_t=q_i,i_{i+1}=q_j|O,λ)
xi = np.zeros((n_states,n_states,n_samples-1))
for t in range(n_samples-1):
denom = np.dot(np.dot(alpha[:,t].T, A) * B[:,observations[t+1]].T, beta[:,t+1])
for i in range(n_states):
numer = alpha[i,t] * A[i,:] * B[:,observations[t+1]].T * beta[:,t+1].T
xi[i,:,t] = numer / denom
# γ_t(i):gamma_t(i) = P(q_t = S_i | O, hmm)
gamma = np.sum(xi,axis=1)
# Need final gamma element for new B
# xi的第三维长度n_samples-1,少一个,所以gamma要计算最后一个
prod = (alpha[:,n_samples-1] * beta[:,n_samples-1]).reshape((-1,1))
gamma = np.hstack((gamma, prod / np.sum(prod))) #append one more to gamma!!!
# 更新模型参数
newpi = gamma[:,0]
newA = np.sum(xi,2) / np.sum(gamma[:,:-1],axis=1).reshape((-1,1))
newB = np.copy(B)
num_levels = B.shape[1]
sumgamma = np.sum(gamma,axis=1)
for lev in range(num_levels):
mask = observations == lev
newB[:,lev] = np.sum(gamma[:,mask],axis=1) / sumgamma
# 检查是否满足阈值
if np.max(abs(pi - newpi)) < criterion and \
np.max(abs(A - newA)) < criterion and \
np.max(abs(B - newB)) < criterion:
done = 1
A[:], B[:], pi[:] = newA, newB, newpi
return newA, newB, newpi
回到预测感冒的问题,下面我们先自己建立一个HMM模型,再模拟出一个观测序列和一个状态序列。
然后,只用观测序列去学习模型,获得模型参数。
In [10]:
A = np.array([[0.5, 0.5],[0.5, 0.5]])
B = np.array([[0.3, 0.3, 0.3],[0.3, 0.3, 0.3]])
pi = np.array([0.5, 0.5])
observations_data, states_data = simulate(100)
newA, newB, newpi = baum_welch_train(observations_data, A, B, pi)
print("newA: ", newA)
print("newB: ", newB)
print("newpi: ", newpi)
newA: [[ 0.5 0.5] [ 0.5 0.5]] newB: [[ 0.28 0.32 0.4 ] [ 0.28 0.32 0.4 ]] newpi: [ 0.5 0.5]
2.3预测问题
考虑到预测问题是求给定观测序列条件概率P(I|O)P(I|O)最大的状态序列I=(i1,i2,...,iT)I=(i1,i2,...,iT),类比这个问题和最短路问题:
我们可以把求P(I|O)P(I|O)的最大值类比成求节点间距离的最小值,于是考虑类似于动态规划的viterbi算法。
首先导入两个变量δδ和ψψ:
定义在时刻tt状态为ii的所有单个路径(i1,i2,i3,...,it)(i1,i2,i3,...,it)中概率最大值为(这里考虑P(I,O)P(I,O)便于计算,因为给定的P(O)P(O),P(I|O)P(I|O)正比于P(I,O)P(I,O)):
δt(i)=maxi1,i2,...,it−1P(it=i,it−1,...,i1,ot,ot−1,...,o1|λ)δt(i)=maxi1,i2,...,it−1P(it=i,it−1,...,i1,ot,ot−1,...,o1|λ)
读作delta,其中,i=1,2,...,Ni=1,2,...,N
得到其递推公式:
δt(i)=max1≤j≤N[δt−1(j)aji]bi(o1)δt(i)=max1≤j≤N[δt−1(j)aji]bi(o1)
定义在时刻tt状态为ii的所有单个路径(i1,i2,i3,...,it−1,i)(i1,i2,i3,...,it−1,i)中概率最大的路径的第t−1t−1个结点为
ψt(i)=argmax1≤j≤N[δt−1(j)aji]ψt(i)=argmax1≤j≤N[δt−1(j)aji]
读作psi,其中,i=1,2,...,Ni=1,2,...,N
下面介绍维特比算法。
维特比(viterbi)算法(动态规划):
输入:模型λ=(A,B,π)λ=(A,B,π)和观测O=(o1,o2,...,oT)O=(o1,o2,...,oT)
输出:最优路径I∗=(i∗1,i∗2,...,i∗T)I∗=(i1∗,i2∗,...,iT∗)
(1).初始化:
δ1(i)=πibi(o1)δ1(i)=πibi(o1)
ψ1(i)=0ψ1(i)=0
(2).递推。对t=2,3,...,Tt=2,3,...,T
δt(i)=max1≤j≤N[δt−1(j)aji]bi(ot)δt(i)=max1≤j≤N[δt−1(j)aji]bi(ot)
ψt(i)=argmax1≤j≤N[δt−1(j)aji]ψt(i)=argmax1≤j≤N[δt−1(j)aji]
(3).终止:
P∗=max1≤i≤NδT(i)P∗=max1≤i≤NδT(i)
i∗T=argmax1≤i≤NδT(i)iT∗=argmax1≤i≤NδT(i)
(4).最优路径回溯,对t=T−1,T−2,...,1t=T−1,T−2,...,1
i∗t=ψt+1(i∗t+1)it∗=ψt+1(it+1∗)
求得最优路径I∗=(i∗1,i∗2,...,i∗T)I∗=(i1∗,i2∗,...,iT∗)
注:上面的bi(ot)bi(ot)和ψt+1(i∗t+1)ψt+1(it+1∗)的括号,并不是函数,而是类似于数组取下标的操作。
viterbi算法python实现(V对应δ,prev对应ψ):
In [11]:
def viterbi(obs_seq, A, B, pi):
"""
Returns
-------
V : numpy.ndarray
V [s][t] = Maximum probability of an observation sequence ending
at time 't' with final state 's'
prev : numpy.ndarray
Contains a pointer to the previous state at t-1 that maximizes
V[state][t]
V对应δ,prev对应ψ
"""
N = A.shape[0]
T = len(obs_seq)
prev = np.zeros((T - 1, N), dtype=int)
# DP matrix containing max likelihood of state at a given time
V = np.zeros((N, T))
V[:,0] = pi * B[:,obs_seq[0]]
for t in range(1, T):
for n in range(N):
seq_probs = V[:,t-1] * A[:,n] * B[n, obs_seq[t]]
prev[t-1,n] = np.argmax(seq_probs)
V[n,t] = np.max(seq_probs)
return V, prev
def build_viterbi_path(prev, last_state):
"""Returns a state path ending in last_state in reverse order.
最优路径回溯
"""
T = len(prev)
yield(last_state)
for i in range(T-1, -1, -1):
yield(prev[i, last_state])
last_state = prev[i, last_state]
def observation_prob(obs_seq):
""" P( entire observation sequence | A, B, pi ) """
return np.sum(forward(obs_seq)[:,-1])
def state_path(obs_seq, A, B, pi):
"""
Returns
-------
V[last_state, -1] : float
Probability of the optimal state path
path : list(int)
Optimal state path for the observation sequence
"""
V, prev = viterbi(obs_seq, A, B, pi)
# Build state path with greatest probability
last_state = np.argmax(V[:,-1])
path = list(build_viterbi_path(prev, last_state))
return V[last_state,-1], reversed(path)
继续感冒预测的例子,根据刚才学得的模型参数,再去预测状态序列,观测准确率。
In [12]:
states_out = state_path(observations_data, newA, newB, newpi)[1]
p = 0.0
for s in states_data:
if next(states_out) == s:
p += 1
print(p / len(states_data))
0.54
因为是随机生成的样本,因此准确率较低也可以理解。
使用Viterbi算法计算病人的病情以及相应的概率:
In [13]:
A = convert_map_to_matrix(transition_probability, states_label2id, states_label2id)
B = convert_map_to_matrix(emission_probability, states_label2id, observations_label2id)
observations_index = [observations_label2id[o] for o in observations]
pi = convert_map_to_vector(start_probability, states_label2id)
V, p = viterbi(observations_index, newA, newB, newpi)
print(" " * 7, " ".join(("%10s" % observations_id2label[i]) for i in observations_index))
for s in range(0, 2):
print("%7s: " % states_id2label[s] + " ".join("%10s" % ("%f" % v) for v in V[s]))
print('\nThe most possible states and probability are:')
p, ss = state_path(observations_index, newA, newB, newpi)
for s in ss:
print(states_id2label[s])
print(p)
normal cold dizzy Healthy: 0.140000 0.022400 0.004480 Fever: 0.140000 0.022400 0.004480 The most possible states and probability are: Healthy Healthy Healthy 0.00448
3.完整代码
代码主要参考Hankcs的博客,hankcs参考的是colostate大学的教学代码。
完整的隐马尔科夫用类包装的代码:
In [15]:
class HMM:
"""
Order 1 Hidden Markov Model
Attributes
----------
A : numpy.ndarray
State transition probability matrix
B: numpy.ndarray
Output emission probability matrix with shape(N, number of output types)
pi: numpy.ndarray
Initial state probablity vector
"""
def __init__(self, A, B, pi):
self.A = A
self.B = B
self.pi = pi
def simulate(self, T):
def draw_from(probs):
"""
1.np.random.multinomial:
按照多项式分布,生成数据
>>> np.random.multinomial(20, [1/6.]*6, size=2)
array([[3, 4, 3, 3, 4, 3],
[2, 4, 3, 4, 0, 7]])
For the first run, we threw 3 times 1, 4 times 2, etc.
For the second, we threw 2 times 1, 4 times 2, etc.
2.np.where:
>>> x = np.arange(9.).reshape(3, 3)
>>> np.where( x > 5 )
(array([2, 2, 2]), array([0, 1, 2]))
"""
return np.where(np.random.multinomial(1,probs) == 1)[0][0]
observations = np.zeros(T, dtype=int)
states = np.zeros(T, dtype=int)
states[0] = draw_from(self.pi)
observations[0] = draw_from(self.B[states[0],:])
for t in range(1, T):
states[t] = draw_from(self.A[states[t-1],:])
observations[t] = draw_from(self.B[states[t],:])
return observations,states
def _forward(self, obs_seq):
"""前向算法"""
N = self.A.shape[0]
T = len(obs_seq)
F = np.zeros((N,T))
F[:,0] = self.pi * self.B[:, obs_seq[0]]
for t in range(1, T):
for n in range(N):
F[n,t] = np.dot(F[:,t-1], (self.A[:,n])) * self.B[n, obs_seq[t]]
return F
def _backward(self, obs_seq):
"""后向算法"""
N = self.A.shape[0]
T = len(obs_seq)
X = np.zeros((N,T))
X[:,-1:] = 1
for t in reversed(range(T-1)):
for n in range(N):
X[n,t] = np.sum(X[:,t+1] * self.A[n,:] * self.B[:, obs_seq[t+1]])
return X
def baum_welch_train(self, observations, criterion=0.05):
"""无监督学习算法——Baum-Weich算法"""
n_states = self.A.shape[0]
n_samples = len(observations)
done = False
while not done:
# alpha_t(i) = P(O_1 O_2 ... O_t, q_t = S_i | hmm)
# Initialize alpha
alpha = self._forward(observations)
# beta_t(i) = P(O_t+1 O_t+2 ... O_T | q_t = S_i , hmm)
# Initialize beta
beta = self._backward(observations)
xi = np.zeros((n_states,n_states,n_samples-1))
for t in range(n_samples-1):
denom = np.dot(np.dot(alpha[:,t].T, self.A) * self.B[:,observations[t+1]].T, beta[:,t+1])
for i in range(n_states):
numer = alpha[i,t] * self.A[i,:] * self.B[:,observations[t+1]].T * beta[:,t+1].T
xi[i,:,t] = numer / denom
# gamma_t(i) = P(q_t = S_i | O, hmm)
gamma = np.sum(xi,axis=1)
# Need final gamma element for new B
prod = (alpha[:,n_samples-1] * beta[:,n_samples-1]).reshape((-1,1))
gamma = np.hstack((gamma, prod / np.sum(prod))) #append one more to gamma!!!
newpi = gamma[:,0]
newA = np.sum(xi,2) / np.sum(gamma[:,:-1],axis=1).reshape((-1,1))
newB = np.copy(self.B)
num_levels = self.B.shape[1]
sumgamma = np.sum(gamma,axis=1)
for lev in range(num_levels):
mask = observations == lev
newB[:,lev] = np.sum(gamma[:,mask],axis=1) / sumgamma
if np.max(abs(self.pi - newpi)) < criterion and \
np.max(abs(self.A - newA)) < criterion and \
np.max(abs(self.B - newB)) < criterion:
done = 1
self.A[:],self.B[:],self.pi[:] = newA,newB,newpi
def observation_prob(self, obs_seq):
""" P( entire observation sequence | A, B, pi ) """
return np.sum(self._forward(obs_seq)[:,-1])
def state_path(self, obs_seq):
"""
Returns
-------
V[last_state, -1] : float
Probability of the optimal state path
path : list(int)
Optimal state path for the observation sequence
"""
V, prev = self.viterbi(obs_seq)
# Build state path with greatest probability
last_state = np.argmax(V[:,-1])
path = list(self.build_viterbi_path(prev, last_state))
return V[last_state,-1], reversed(path)
def viterbi(self, obs_seq):
"""
Returns
-------
V : numpy.ndarray
V [s][t] = Maximum probability of an observation sequence ending
at time 't' with final state 's'
prev : numpy.ndarray
Contains a pointer to the previous state at t-1 that maximizes
V[state][t]
"""
N = self.A.shape[0]
T = len(obs_seq)
prev = np.zeros((T - 1, N), dtype=int)
# DP matrix containing max likelihood of state at a given time
V = np.zeros((N, T))
V[:,0] = self.pi * self.B[:,obs_seq[0]]
for t in range(1, T):
for n in range(N):
seq_probs = V[:,t-1] * self.A[:,n] * self.B[n, obs_seq[t]]
prev[t-1,n] = np.argmax(seq_probs)
V[n,t] = np.max(seq_probs)
return V, prev
def build_viterbi_path(self, prev, last_state):
"""Returns a state path ending in last_state in reverse order."""
T = len(prev)
yield(last_state)
for i in range(T-1, -1, -1):
yield(prev[i, last_state])
last_state = prev[i, last_state]