图像处理——相机标定（Camera calibration）

非常感谢以下四位的渊博知识：

（1）牧野-           https://blog.csdn.net/dcrmg/article/details/52939318

（2）chaooooooo https://blog.csdn.net/chao56789/article/details/47040285

（3）jason_ql  https://blog.csdn.net/lql0716/article/details/71973318?locationNum=8&fps=1

（4）holybin        https://blog.csdn.net/holybin/article/details/41122493

一、相机标定（Camera calibration）原理

• 在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定（或摄像机标定）。无论是在图像测量或者机器视觉应用中，相机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此，做好相机标定是做好后续工作的前提，提高标定精度是科研工作的重点所在。

• 常用术语
  内参矩阵: Intrinsic Matrix
  焦距: Focal Length
  主点: Principal Point
  径向畸变: Radial Distortion
  切向畸变: Tangential Distortion
  旋转矩阵: Rotation Matrices
  平移向量: Translation Vectors
  平均重投影误差: Mean Reprojection Error
  重投影误差: Reprojection Errors
  重投影点: Reprojected Points

1、坐标系的转换

1.1 世界坐标系

世界坐标系（world coordinate）(xw,yw,zw)，也称为测量坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。

1.2 相机坐标系

相机坐标系（camera coordinate）(xc,yc,zc)，也是一个三维直角坐标系，原点位于镜头光心处，x、y轴分别与相面的两边平行，z轴为镜头光轴，与像平面垂直。

1.3 世界坐标系转换为相机坐标系

1.4 像素坐标系、图像坐标系

• 图1：
  

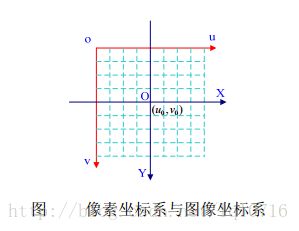
• 像素坐标系（pixel coordinate）
  如图1，像素坐标系uov是一个二维直角坐标系，反映了相机CCD/CMOS芯片中像素的排列情况。原点o位于图像的左上角，u轴、v轴分别于像面的两边平行。像素坐标系中坐标轴的单位是像素（整数）。

像素坐标系不利于坐标变换，因此需要建立图像坐标系XOY，其坐标轴的单位通常为毫米（mm），原点是相机光轴与相面的交点（称为主点），即图像的中心点，X轴、Y轴分别与u轴、v轴平行。故两个坐标系实际是平移关系，即可以通过平移就可得到。

• 

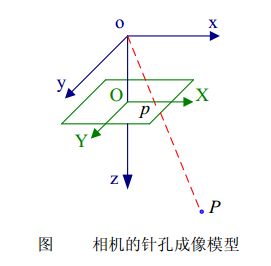
1.5 针孔成像原理

图2：

1.6 世界坐标系转换为像素坐标系

2 相机内参与畸变参数

2.1 相机内参

• 参看1.6节所述

2.2 畸变参数

• 畸变参数(distortion parameters)

  畸变（distortion）是对直线投影（rectilinear projection）的一种偏移。

  简单来说直线投影是场景内的一条直线投影到图片上也保持为一条直线。

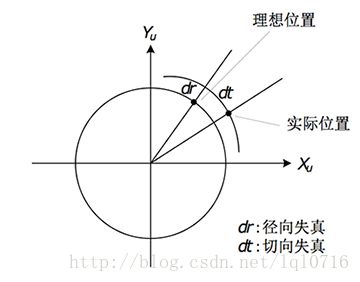
  畸变简单来说就是一条直线投影到图片上不能保持为一条直线了，这是一种光学畸变（optical aberration）,可能由于摄像机镜头的原因。

• 畸变一般可以分为：径向畸变、切向畸变

  1、径向畸变来自于透镜形状
  2、切向畸变来自于整个摄像机的组装过程

  畸变还有其他类型的畸变，但是没有径向畸变、切向畸变显著

• 畸变图示
  

• 径向畸变

  实际摄像机的透镜总是在成像仪的边缘产生显著的畸变，这种现象来源于“筒形”或“鱼眼”的影响。

  如下图，光线在远离透镜中心的地方比靠近中心的地方更加弯曲。对于常用的普通透镜来说，这种现象更加严重。筒形畸变在便宜的网络摄像机中非常厉害，但在高端摄像机中不明显，因为这些透镜系统做了很多消除径向畸变的工作。
  

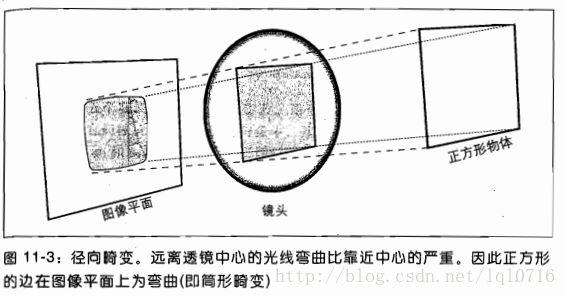
  对于径向畸变，成像仪中心（光学中心）的畸变为0，随着向边缘移动，畸变越来越严重。

• 径向畸变包括：枕形畸变、桶形畸变

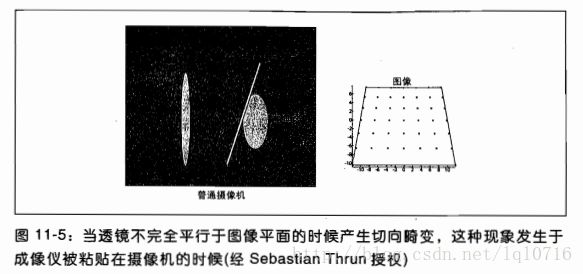
• 切向畸变

  • 切向畸变是由于透镜制造上的缺陷使得透镜本身与图像平面不平行而产生的。

  • 切向畸变可分为：薄透镜畸变、离心畸变

  • 切向畸变图示：
    

二、张正友相机标定

张正友的方法只考虑了径向畸变，没有考虑切向畸变

相机标定的目的：获取摄像机的内参和外参矩阵（同时也会得到每一幅标定图像的旋转和平移矩阵），内参和外参系数可以对之后相机拍摄的图像进行矫正，得到畸变相对很小的图像。

相机标定的输入：标定图像上所有内角点的图像坐标，标定板图像上所有内角点的空间三维坐标（一般情况下假定图像位于Z=0平面上）。

相机标定的输出：摄像机的内参、外参系数。

这三个基础的问题就决定了使用Opencv实现张正友法标定相机的标定流程、标定结果评价以及使用标定结果矫正原始图像的完整流程：

1. 准备标定图片

2. 对每一张标定图片，提取角点信息

3. 对每一张标定图片，进一步提取亚像素角点信息

4. 在棋盘标定图上绘制找到的内角点（非必须，仅为了显示）

5. 相机标定

6. 对标定结果进行评价

7. 查看标定效果——利用标定结果对棋盘图进行矫正

1. 准备标定图片

标定图片需要使用标定板在不同位置、不同角度、不同姿态下拍摄，最少需要3张，以10~20张为宜。标定板需要是黑白相间的矩形构成的棋盘图，制作精度要求较高，如下图所示：

2.对每一张标定图片，提取角点信息

需要使用findChessboardCorners函数提取角点，这里的角点专指的是标定板上的内角点，这些角点与标定板的边缘不接触。

FindChessboardCorners是opencv的一个函数，可以用来寻找棋盘图的内角点位置。

函数形式

int cvFindChessboardCorners( const void* image, CvSize pattern_size, CvPoint2D32f* corners, int* corner_count=NULL, int flags=CV_CALIB_CB_ADAPTIVE_THRESH );

参数说明

Image:

输入的棋盘图，必须是8位的灰度或者彩色图像。

pattern_size:

棋盘图中每行和每列角点的个数。这里是内角点的行列数，不包括边缘角点行列数；行数和列数不要相同，这样的话函数会辨别出标定板的方向，如果行列数相同，那么函数每次画出来的角点起始位置会变化，不利于标定。

Corners:

检测到的角点

corner_count:

输出，角点的个数。如果不是NULL，函数将检测到的角点的个数存储于此变量。

Flags:

各种操作标志，可以是0或者下面值的组合：

CV_CALIB_CB_ADAPTIVE_THRESH：该函数的默认方式是根据图像的平均亮度值进行图像二值化，设立此标志位的含义是采用变化的阈值进行自适应二值化；
CV_CALIB_CB_NORMALIZE_IMAGE：在二值化之前，调用EqualizeHist()函数进行图像归一化处理；
CV_CALIB_CB_FILTER_QUADS：二值化完成后，函数开始定位图像中的四边形（这里不应该称之为正方形，因为存在畸变），这个标志设立后，函数开始使用面积、周长等参数来筛选方块，从而使得角点检测更准确更严格。

CALIB_CB_FAST_CHECK：快速检测选项，对于检测角点极可能不成功检测的情况，这个标志位可以使函数效率提升。

总结：该函数的功能就是判断图像内是否包含完整的棋盘图，如果能够检测完全，就把他们的角点坐标按顺序（逐行，从左到右）记录下来，并返回非0数，否则返回0。这里对size参数要求非常严格，函数必须检测到相同的size才会返回非0，否则返回0，这里一定要注意。角点检测不完全时，可能画不出图像，或者画出红色角点；正确的图像后面有参考。

补充说明

函数cvFindChessboardCorners试图确定输入图像是否是棋盘模式，并确定角点的位置。如果所有角点都被检测到且它们都被以一定顺序排布，函数返回非零值，否则在函数不能发现所有角点或者记录它们地情况下，函数返回0。例如一个正常地棋盘图右8x8个方块和7x7个内角点，内角点是黑色方块相互联通的位置。这个函数检测到地坐标只是一个大约的值，如果要精确地确定它们的位置，可以使用函数cvFindCornerSubPix。

 

函数测试：

测试图像（左）和运行结果（右）

图像均为640*360的8*8黑白格棋盘图，7*7个内点。

• 图1.计算机图像，成功检测出所有49个角点，顺序以行从左上到右下
• 图2.正面实拍图像，检测出48个角点，其中正确47个，错误一个，没有标记顺序，只标记位置
• 图3.正面实拍图像，成功检测出所有49个角点，顺序以行从左上到右下
• 图4.侧面实拍图像，成功检测出所有49个角点，顺序以列从右上到坐下

结果分析：

• 1图与3图，角特性良好，正面拍摄，函数顺利找到角点位置
• 2图中，未检测出的右上角两个角点可能是由于胶带干扰，角特征变的不明显。检测到的错误点是因为背景图像中有黑色物体，导致计算机误认为其为黑色方格。
• 4图中，由于拍摄角度倾斜，棋盘图像发生变形，角点查找顺序发生变化。可以通过重新排列矩阵Corners的大小来得到1图与3图同样的效果

3. 对每一张标定图片，进一步提取亚像素角点信息

为了提高标定精度，需要在初步提取的角点信息上进一步提取亚像素信息，降低相机标定偏差，常用的方法是cornerSubPix，另一个方法是使用find4QuadCornerSubpix函数，这个方法是专门用来获取棋盘图上内角点的精确位置的。

cornerSubPix()函数

（1）函数原型

cornerSubPix()函数在角点检测中精确化角点位置，其函数原型如下：

void cornerSubPix(InputArray image, InputOutputArray corners, Size winSize, Size zeroZone, TermCriteria criteria);

（2）函数参数

函数参数说明如下：

image：输入图像

corners：输入角点的初始坐标以及精准化后的坐标用于输出。

winSize：搜索窗口边长的一半，例如如果winSize=Size(5,5)，则一个大小为的搜索窗口将被使用。

zeroZone：搜索区域中间的dead region边长的一半，有时用于避免自相关矩阵的奇异性。如果值设为(-1,-1)则表示没有这个区域。
criteria：角点精准化迭代过程的终止条件。也就是当迭代次数超过criteria.maxCount，或者角点位置变化小于criteria.epsilon时，停止迭代过程。

在其中一个标定的棋盘图上分别运行cornerSubPix和find4QuadCornerSubpix寻找亚像素角点，两者定位到的亚像素角点坐标分别为：

   cornerSubPix：                                                 find4QuadCornerSubpix：

                       

虽然有一定差距，但偏差基本都控制在0.5个像素之内。

4. 在棋盘标定图上绘制找到的内角点（非必须，仅为了显示）

drawChessboardCorners函数用于绘制被成功标定的角点，函数原型：

CV_EXPORTS_W void drawChessboardCorners( InputOutputArray image, Size patternSize,
                                         InputArray corners, bool patternWasFound );

第一个参数image，8位灰度或者彩色图像；

第二个参数patternSize，每张标定棋盘上内角点的行列数；

第三个参数corners，初始的角点坐标向量，同时作为亚像素坐标位置的输出，所以需要是浮点型数据，一般用元素是Pointf2f/Point2d的向量来表示：vector iamgePointsBuf；

第四个参数patternWasFound，标志位，用来指示定义的棋盘内角点是否被完整的探测到，true表示别完整的探测到，函数会用直线依次连接所有的内角点，作为一个整体，false表示有未被探测到的内角点，这时候函数会以（红色）圆圈标记处检测到的内角点；

5. 相机标定

获取到棋盘标定图的内角点图像坐标之后，就可以使用calibrateCamera函数进行标定，计算相机内参和外参系数。

calibrateCamera函数原型：

double calibrateCamera(InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints,Size imageSize, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, int flags=0)

其中objectPoints为世界坐标系中的点。在使用时，应该输入一个三维点的vector的vector，即vector> objectPoints。

imagePoints为其对应的图像点。和objectPoints一样，应该输入std::vector> imagePoints型的变量。

imageSize为图像的大小，在计算相机的内参数和畸变矩阵需要用到；

cameraMatrix为内参数矩阵。输入一个cv::Mat cameraMatrix即可。

distCoeffs为畸变矩阵。输入一个cv::Mat distCoeffs即可。

rvecs为旋转向量；应该输入一个cv::Mat的vector，即vector rvecs因为每个vector会得到一个rvecs。

tvecs为位移向量；和rvecs一样，也应该为vector tvecs。

flags为标定是所采用的算法。可如下某个或者某几个参数：

CV_CALIB_USE_INTRINSIC_GUESS：使用该参数时，在cameraMatrix矩阵中应该有fx,fy,cx,cy的估计值。否则的话，将初始化(cx,cy）图像的中心点，使用最小二乘估算出fx，fy。如果内参数矩阵和畸变居中已知的时候，应该标定模块中的solvePnP()函数计算外参数矩阵。

CV_CALIB_FIX_PRINCIPAL_POINT：在进行优化时会固定光轴点。当CV_CALIB_USE_INTRINSIC_GUESS参数被设置，光轴点将保持在中心或者某个输入的值。

CV_CALIB_FIX_ASPECT_RATIO：固定fx/fy的比值，只将fy作为可变量，进行优化计算。当CV_CALIB_USE_INTRINSIC_GUESS没有被设置，fx和fy将会被忽略。只有fx/fy的比值在计算中会被用到。

CV_CALIB_ZERO_TANGENT_DIST：设定切向畸变参数（p1,p2）为零。

CV_CALIB_FIX_K1,...,CV_CALIB_FIX_K6：对应的径向畸变在优化中保持不变。如果设置了CV_CALIB_USE_INTRINSIC_GUESS参数，

CV_CALIB_RATIONAL_MODEL：计算k4，k5，k6三个畸变参数。如果没有设置，则只计算其它5个畸变参数。

在使用calibrateCamera标定前，一般使用findChessboardCorners()函数获得棋盘标定板的角点位置。

还需要注意的是，在目前的opencv版本中(opencv2.4)，当需要计算获得内参数矩阵时，即不使用CV_CALIB_USE_INTRINSIC_GUESS参数时，要求输入的objectPoints的为平面标定模式，即Z轴都为零。否则会出错。

如果对calibrateCamera的详细算法感兴趣，可以阅读张正友的标定算法A Flexible New Technique for Camera Calibration。可以从google scholar上搜索下载。

6. 对标定结果进行评价

对标定结果进行评价的方法是通过得到的摄像机内外参数，对空间的三维点进行重新投影计算，得到空间三维点在图像上新的投影点的坐标，计算投影坐标和亚像素角点坐标之间的偏差，偏差越小，标定结果越好。

对空间三维坐标点进行反向投影的函数是projectPoints，函数原型是：

//! projects points from the model coordinate space to the image coordinates. Also computes derivatives of the image coordinates w.r.t the intrinsic and extrinsic camera parameters
CV_EXPORTS_W void projectPoints( InputArray objectPoints,
                                 InputArray rvec, InputArray tvec,
                                 InputArray cameraMatrix, InputArray distCoeffs,
                                 OutputArray imagePoints,
                                 OutputArray jacobian=noArray(),
                                 double aspectRatio=0 );

第一个参数objectPoints，为相机坐标系中的三维点坐标；

第二个参数rvec为旋转向量，每一张图像都有自己的选择向量；

第三个参数tvec为位移向量，每一张图像都有自己的平移向量；

第四个参数cameraMatrix为求得的相机的内参数矩阵；

第五个参数distCoeffs为相机的畸变矩阵；

第六个参数iamgePoints为每一个内角点对应的图像上的坐标点；

第七个参数jacobian是雅可比行列式；

第八个参数aspectRatio是跟相机传感器的感光单元有关的可选参数，如果设置为非0，则函数默认感光单元的dx/dy是固定的，会依此对雅可比矩阵进行调整；

下边显示了某一张标定图片上的亚像素角点坐标和根据标定结果把空间三维坐标点映射回图像坐标点的对比：

find4QuadCornerSubpix查找到的亚像素点坐标：                           projectPoints映射的坐标：

                                                     

以下是每一幅图像上24个内角点的平均误差统计数据：

7. 查看标定效果——利用标定结果对棋盘图进行矫正

利用求得的相机的内参和外参数据，可以对图像进行畸变的矫正，这里有两种方法可以达到矫正的目的，分别说明一下。

方法一：使用initUndistortRectifyMap和remap两个函数配合实现。

initUndistortRectifyMap用来计算畸变映射，remap把求得的映射应用到图像上。

initUndistortRectifyMap的函数原型：

//! initializes maps for cv::remap() to correct lens distortion and optionally rectify the image
CV_EXPORTS_W void initUndistortRectifyMap( InputArray cameraMatrix, InputArray distCoeffs,
                           InputArray R, InputArray newCameraMatrix,
                           Size size, int m1type, OutputArray map1, OutputArray map2 );

第一个参数cameraMatrix为之前求得的相机的内参矩阵；

第二个参数distCoeffs为之前求得的相机畸变矩阵；

第三个参数R，可选的输入，是第一和第二相机坐标之间的旋转矩阵；

第四个参数newCameraMatrix，输入的校正后的3X3摄像机矩阵；

第五个参数size，摄像机采集的无失真的图像尺寸；

第六个参数m1type，定义map1的数据类型，可以是CV_32FC1或者CV_16SC2；

第七个参数map1和第八个参数map2，输出的X/Y坐标重映射参数；

remap函数原型：

//! warps the image using the precomputed maps. The maps are stored in either floating-point or integer fixed-point format
CV_EXPORTS_W void remap( InputArray src, OutputArray dst,
                         InputArray map1, InputArray map2,
                         int interpolation, int borderMode=BORDER_CONSTANT,
                         const Scalar& borderValue=Scalar());

第一个参数src，输入参数，代表畸变的原始图像；

第二个参数dst，矫正后的输出图像，跟输入图像具有相同的类型和大小；

第三个参数map1和第四个参数map2，X坐标和Y坐标的映射；

第五个参数interpolation，定义图像的插值方式；

第六个参数borderMode，定义边界填充方式；

方法二：使用undistort函数实现

undistort函数原型：

//! corrects lens distortion for the given camera matrix and distortion coefficients
CV_EXPORTS_W void undistort( InputArray src, OutputArray dst,
                             InputArray cameraMatrix,
                             InputArray distCoeffs,
                             InputArray newCameraMatrix=noArray() );

第一个参数src，输入参数，代表畸变的原始图像；

第二个参数dst，矫正后的输出图像，跟输入图像具有相同的类型和大小；

第三个参数cameraMatrix为之前求得的相机的内参矩阵；

第四个参数distCoeffs为之前求得的相机畸变矩阵；

第五个参数newCameraMatrix，默认跟cameraMatrix保持一致；

方法一相比方法二执行效率更高一些，推荐使用。