文档排序--相似度模型--VSM

说明：文章内容来源于课程视频和课程ppt。我只学习了课程没有做习题。文章不是翻译，是我对课程的理解。

---

　上文提到文档排序函数是TR的核心。文档排序函数的实现有几种思路，其中一种是基于相似度的模型。这种模型具体是用空间向量模型(Vector Space Model)实现。这篇文章就介绍VSM。

VSM概念

什么是VSM

　
　VSM定义了两点。
　第一，用词向量(term vector)来表示查询语句、表示文档。英文中的term vector，我们翻译为词向量。但是这里的“词”并不是指汉语中的一个词，具体含义是：基本概念，可以是一个字、一个词、一个短语。每个词表示一个维度，N个词就可以定义N维空间。如上图所示，programming,libarary,presidential，分别定义了三个维度。查询语句的向量表示： q=(x1,x2,...xN) q = ( x 1 , x 2 , . . . x N ) ，文档的向量表示： d=(y1,y2,...yN) d = ( y 1 , y 2 , . . . y N ) 。
　第二，查询语句和文档的相关度正比于查询语句和文档的相似度： relevance(q,d)∝similarity(q,d)=f(q,d) r e l e v a n c e ( q , d ) ∝ s i m i l a r i t y ( q , d ) = f ( q , d )

VSM没有定义的

　1 怎么定义或者说怎么选择term。只说term是文档集中的基本概念，并未指明什么可以作为term。
　2 向量的表示。用什么值来计算查询向量和文档向量。
　3 相似度怎么计算。
　基于以上几点说VSM其实是一个框架frame。在实践中有好多版本的实现。继续往下看。

VSM实现

　来源于ppt的例子。
　query=”news about presidential campaign”
　d1:”… news about …”
　d2:”… news about organic food campaign…”
　d3:”… news of presidential campaign …”
　d4:”… news of presidential campaign … … presidential candidate …”
　d5:”… news of organic food campaign… campaign…campaign…campaign…”

　在这个例子中很理想的排序大概应该是：d4,d3。d1,d2,d5其实是不相关文档。

简单实现

　BOW+bit-vector+dotproduct 这是一个最简单的实现。
　1 用文档中的每一个词定义一个维度。称为词袋模型(Bag of Word=BOW)。
　2 用Bit-Vector 表示向量。如果词出现则记为1，否则为0。 xi,yi∈{0,1} x i , y i ∈ { 0 , 1 } 。
　3 相似度通过点积(dot product)计算。
　最终表示
　 q=(x1,x2....yn),xi∈{0,1} q = ( x 1 , x 2 . . . . y n ) , x i ∈ { 0 , 1 }
　 d=(y1,y2...yn),yi∈{0,1} d = ( y 1 , y 2 . . . y n ) , y i ∈ { 0 , 1 }
　 sim(q,d)=x1y1+x2y2+....+xNyN=∑Ni=1xiyi s i m ( q , d ) = x 1 y 1 + x 2 y 2 + . . . . + x N y N = ∑ i = 1 N x i y i
　
　计算一下例子。
　V= {news, about, presidential, campaign, food …. }
　q= (1, 1, 1, 1, 0, …)
　d1= (1, 1, 0, 0, 0, …)
　d2= (1, 1, 0, 1, 0, …)
　d3= (1, 0, 1, 1, 0, …)
　…
　f(q,d1)=1*1+1*1+0…=2
　f(q,d2)=1*1+1*1+0+1*1+…=3
　…
　本算法中sim(q,d)函数的实质就是表示有多少个不同的查询词出现在文档中。
　在d2,d3,d4文档中各出现了3次，值为3,；在d1,d5文档中各出现了2次，值为2。

进阶实现

　BOW+term frequency+dotproduct
　问题：d4中 “presidential ”的次数要比d2多，应该排在前面才对。
　解决策略就是使用词频这个信息。
　最终表示
　 q=(x1,x2....yn),xi q = ( x 1 , x 2 . . . . y n ) , x i 是词 wi w i 在查询语句中出现次数
　 d=(y1,y2...yn),yi d = ( y 1 , y 2 . . . y n ) , y i 是词 wi w i 在文档中出现次数
　 sim(q,d)=x1y1+x2y2+....+xNyN=∑Ni=1xiyi s i m ( q , d ) = x 1 y 1 + x 2 y 2 + . . . . + x N y N = ∑ i = 1 N x i y i
　
　计算一下例子。
　f(q,d4)=1*1+1*0+1*2+1*1+0+…=4
　f(q,d2)=….
　….
　
　

TD-IDF

　BOW+TF-IDF+dotproduct
　
　
　问题：d2与d3，虽然都命中3个词，但是显然命中presidential比命中about得分要高。presidential含有更重要的信息嘛。
　解决策略：使用逆文档频率IDF，在越多文档中出现，权重越低。
　 IDF=logM+1k I D F = l o g M + 1 k ，M是文档集中文档数量，k是词在多少个文档中出现。
　
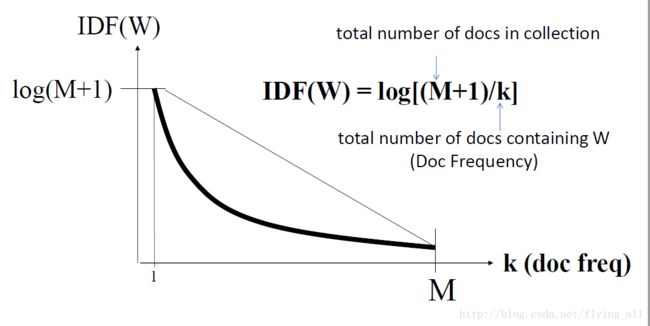
　可以看到当k=1的时候，IDF=log(M+1)；当k=M的时候IDF接近0。
　
　最终表示
　 q=(x1,x2....yn),xi q = ( x 1 , x 2 . . . . y n ) , x i 是词 wi w i 在查询语句中出现次数
　 d=(y1,y2...yn),yi=c(wi,d)∗IDF(wi)，c(wi,d) d = ( y 1 , y 2 . . . y n ) , y i = c ( w i , d ) ∗ I D F ( w i ) ， c ( w i , d ) 是 wi w i 在文档中的出现次数， IDF(wi) I D F ( w i ) 是 wi w i 在整个文档集中的逆文档频率。
　 sim(q,d)=x1y1+x2y2+....+xNyN=∑Ni=1xiyi s i m ( q , d ) = x 1 y 1 + x 2 y 2 + . . . . + x N y N = ∑ i = 1 N x i y i
　
　计算例子
　V= {news, about, presidential, campaign, food …. }
　IDF(W)= 1.5 1.0 2.5 3.1 1.8
　f(q,d2)=5.6 ， f(q,d3)=7.1问题解决。但是f(q,d5)=13.9。我们在最开始就分析了排在前面的文档应该是d4，d3。
　

TF变形

　 sim(q,d)=f(q,d)=∑Ni=1xiyi=∑w∈q∩dc(w,q)c(w,d)logM+1df(w) s i m ( q , d ) = f ( q , d ) = ∑ i = 1 N x i y i = ∑ w ∈ q ∩ d c ( w , q ) c ( w , d ) l o g M + 1 d f ( w ) ,df(w)是指词w的文档量。
　问题：d5的打分太高了：13.9，分值高是因为“campaign”的频率太高。当一个词从无到有，有重要价值。但一个文档中包含某个词3-5次，与10次基本上不会有太大差异。所以要适当降低词频的影响。
　解决方法1：被称为“亚线性变换(Sublinear TF Transformation)”。使用log函数。函数1： y=x y = x ，函数2： y=log(1+x) y = l o g ( 1 + x ) ，函数1的增长率要比函数2大多了。
　

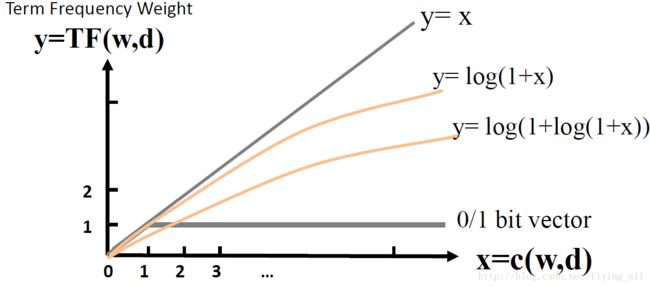
　 f(q,d)=∑w∈q∩dc(w,q)ln[1+c(w,d)]logM+1df(w) f ( q , d ) = ∑ w ∈ q ∩ d c ( w , q ) l n [ 1 + c ( w , d ) ] l o g M + 1 d f ( w )
　

　解决方法2：被称为“BM25变换”。这种变换需要为词频设置一个最大值。假设最大值为6，超过6的词频都没有区别。函数 y=(k+1)xx+k y = ( k + 1 ) x x + k ，函数值会无线接近于k+1。实践证明BM25变换是非常健壮和有效的(robust and effective)。
　
　

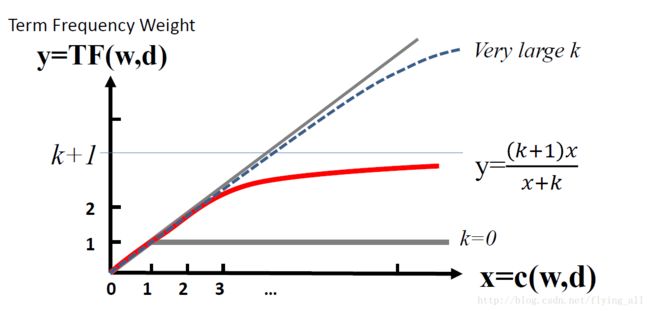
　 f(q,d)=∑w∈q∩dc(w,q)(k+1)c(w,d)c(w,d)+klogM+1df(w) f ( q , d ) = ∑ w ∈ q ∩ d c ( w , q ) ( k + 1 ) c ( w , d ) c ( w , d ) + k l o g M + 1 d f ( w )

文档长度变形

　问题：当一个文档很长的时候，会更容易出现一个词，一个词的频率也更可能高。所以我们需要惩罚一下长文档。一个文档很长可能因为两个原因：一种是文档内容很详细，做了很多必要的描述；还有一种情况是一个大的文档中讲述了很多内容，每个内容一个小的段落，这样的文档其实是一个一个的小文档。在第二种情况中，词的相关度计算出来是不同的：从长文档中计算与从短文档中计算。
　
　解决：算法称为Pivoted Length Normalization。这里同样也有一个参数需要选择：平均文档长度avdl。函数： normalizer=1−b+bdavdl n o r m a l i z e r = 1 − b + b d a v d l ，参数b是惩罚因子， b∈[0,1] b ∈ [ 0 , 1 ] 。
　
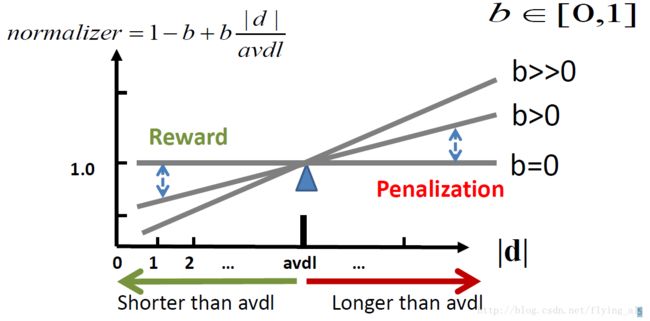
　normalizer会放在相似度函数 f(q,d) f ( q , d ) 的分母上。
　当b=0，所有值都为1，没有惩罚。
　当b>0，当文档长度 < < avdl，normalizer<1，f(q,d)会增加；当文档产度>avdl，normalizer>1，f(q,d)会减小。
　
　最后的公式
　TF亚线性变换： f(q,d)=∑w∈q∩dc(w,q)ln[1+c(w,d)]1−b+bdavdllogM+1df(w) f ( q , d ) = ∑ w ∈ q ∩ d c ( w , q ) l n [ 1 + c ( w , d ) ] 1 − b + b d a v d l l o g M + 1 d f ( w )
　BM25变换： f(q,d)=∑w∈q∩dc(w,q)(k+1)c(w,d)c(w,d)+k(1−b+bdavdl)logM+1df(w) f ( q , d ) = ∑ w ∈ q ∩ d c ( w , q ) ( k + 1 ) c ( w , d ) c ( w , d ) + k ( 1 − b + b d a v d l ) l o g M + 1 d f ( w )
　这一部分其实没怎么明白。我再查查资料。既然是改变词频那直接写为 c(w,d)1−b+bdavdl c ( w , d ) 1 − b + b d a v d l 不就可以了吗？为什么不是这种形式。
　考虑文档长度其实是把词频转为词频率，便于比较。

如何进一步提高VSM的效果

　从词的维度改进。例如可以去掉停止词、做词的变换(stemmed words)、使用短语、语义索引、n元模型等待。
　改进相似度函数。例如可以用欧式距离、用余弦距离表示相似度。实践中证明点积还是最适合的。