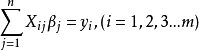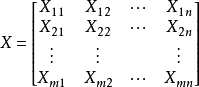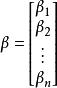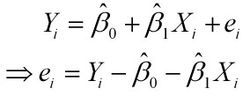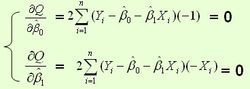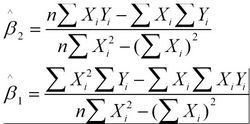最小二乘法
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
===============举例===============================================
线性最小二乘的基本公式
其中m代表有m个等式,n代表有 n 个未知数 ![]() ,m>n ;将其进行向量化后为:
,m>n ;将其进行向量化后为:![]()
显然该方程组一般而言没有解,所以为了选取最合适的 ![]() 让该等式"尽量成立",引入残差平方和函数S
让该等式"尽量成立",引入残差平方和函数S
![]()
(在统计学中,残差平方和函数可以看成n倍的均方误差MSE)
当 ![]() 时,
时,![]() 取最小值,记作:
取最小值,记作:![]()
那![]() 怎么求?等下一行有方法,运用线性代数就可以解出
怎么求?等下一行有方法,运用线性代数就可以解出![]()
通过对 ![]() 进行微分 [2] 求最值,可以得到:
进行微分 [2] 求最值,可以得到:![]()
如果矩阵 ![]() 非奇异,则
非奇异,则 ![]() 有唯一解 [3] :
有唯一解 [3] :![]()
===========原理分析=========
原理
在我们研究两个变量(x,y)之间的相互关系时,通常可以得到一系列成对的数据(x1,y1.x2,y2... xm,ym);将这些数据描绘在x -y直角坐标系中,若发现这些点在一条直线附近,可以令这条直线方程如(式1-1)。
![]() (式1-1)
(式1-1)
其中:a0、a1 是任意实数
为建立这直线方程就要确定a0和a1,应用《最小二乘法原理》,将实测值Yi与利用计算值Yj(Yj=a0+a1Xi)(式1-1)的离差(Yi-Yj)的平方和 ![]() 最小为“优化判据”。
最小为“优化判据”。
令:φ = ![]() (式1-2)
(式1-2)
把(式1-1)代入(式1-2)中得:
φ =![]() (式1-3)
(式1-3)
当 ![]() 最小时,可用函数 φ 对a0、a1求偏导数,令这两个偏导数等于零。实测值Yi:
最小时,可用函数 φ 对a0、a1求偏导数,令这两个偏导数等于零。实测值Yi: ![]() (式1-1)
(式1-1)
因为φ取得最小,则计算值Yj近似于实测值Yi。但通过上面方法可求得实测值Yi即可等价表示预测函数Yj。一举两得。
∑2(a0 + a1*Xi - Yi)=0(式1-4)
∑2Xi(a0 +a1*Xi - Yi)=0(式1-5)
亦即:
na0 + (∑Xi ) a1 = ∑Yi (式1-6)
(∑Xi ) a0 + (∑Xi^2 ) a1 = ∑(Xi*Yi) (式1-7)
得到的两个关于a0、 a1为未知数的两个方程组,解这两个方程组得出:
a0 = (∑Yi) / n - a1(∑Xi) / n (式1-8)
a1 = [n∑(Xi Yi) - (∑Xi ∑Yi)] / (n∑Xi^2 -∑Xi∑Xi)(式1-9)
这时把a0、a1代入(式1-1)中, 此时的(式1-1)就是我们回归的一元线性方程即:数学模型。
在回归过程中,回归的关联式不可能全部通过每个回归数据点(x1,y1. x2,y2...xm,ym),为了判断关联式的好坏,可借助相关系数“R”,统计量“F”,剩余标准偏差“S”进行判断;“R”越趋近于 1 越好;“F”的绝对值越大越好;“S”越趋近于 0 越好。
R = [∑XiYi - m (∑Xi / m)(∑Yi / m)]/ SQR{[∑Xi2 - m (∑Xi / m)2][∑Yi2 - m (∑Yi / m)2]} (式1-10) *
在(式1-10)中,m为样本容量,即实验次数;Xi、Yi分别为任意一组实验数据X、Y的数值。 [1]
==============深度学习中=========
方法
以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢?监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面。 [4]
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择: [4]
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
(2)用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
(3)最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外,得到的估计量还具有优良特性。这种方法对异常值非常敏感。 [4]
最常用的是普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小。(Q为残差平方和)- 即平方损失函数。 [4]
样本回归模型:
其中ei为样本(Xi,Yi)的误差。 [4]
平方损失函数:
则通过Q最小确定这条直线,即确定β0和β1,把它们看作是Q的函数,就变成了一个求极值的问题,可以通过求导数得到。求Q对两个待估参数的偏导数: [4]
根据数学知识我们知道,函数的极值点为偏导为0的点。 因为它是凹函数,凹函数极值点就是偏导数的为0的点[4]
定理1(必要条件) 设函数![]() 在点
在点![]() 具有偏导数,且在点
具有偏导数,且在点![]() 处有极值,则它在该点的偏导数必然为零
处有极值,则它在该点的偏导数必然为零
凡是能使![]() 同时成立的点
同时成立的点![]() 称为函数
称为函数![]() 的驻点,从定理1可知,具有偏导数的函数的极值点必定是驻点。但是函数的驻点不一定是极值点
的驻点,从定理1可知,具有偏导数的函数的极值点必定是驻点。但是函数的驻点不一定是极值点
解得:
这就是最小二乘法的解法,就是求得平方损失函数的极值点。因为我们的函数是凹函数,所以是极小值点。可以等价近似于
真实函数即预测函数。
二、条件极值 拉格朗日乘数法,利用拉格朗日乘数法求条件极值
拉格朗日乘数法 要找函数![]() 在附加条件
在附加条件![]() 下的可能极值点,可以先构成辅助函数
下的可能极值点,可以先构成辅助函数
![]()
其中![]() 为某一常数求其对
为某一常数求其对![]() 与
与![]() 的一阶偏导数,并使之为零,然后与方程(2)联立
的一阶偏导数,并使之为零,然后与方程(2)联立
由这方程组解出![]() ,
,![]() 及
及![]() ,则其中
,则其中![]() ,
,![]() 就是函数
就是函数![]() 在附加条件下
在附加条件下![]() 的可能极值点的坐标。
的可能极值点的坐标。
=================总结============
公式
![]()
拟合
对给定数据点集合 ![]() ,在取定的函数类
,在取定的函数类 ![]() 中,求
中,求 ![]() ,使误差的平方和
,使误差的平方和 ![]() 最小,
最小,
![]()
。从几何意义上讲,就是寻求与给定点集 ![]() 的距离平方和为最小的曲线y=p(x)。函数p(x)称为拟合函数或最小二乘解,求拟合函数p(x)的方法称为曲线拟合的最小二乘法。 [1]
的距离平方和为最小的曲线y=p(x)。函数p(x)称为拟合函数或最小二乘解,求拟合函数p(x)的方法称为曲线拟合的最小二乘法。 [1]
最小二乘法的矩阵形式
最小二乘法的矩阵形式为:![]()
其中 ![]() 为
为 ![]() 的矩阵,
的矩阵, ![]() 为
为 ![]() 的列向量,
的列向量, ![]() 为
为 ![]() 的列向量。如果
的列向量。如果 ![]()
(方程的个数大于未知量的个数),这个方程系统称为矛盾方程组(Over Determined System),如果 ![]()
(方程的个数小于未知量的个数),这个系统就是Under Determined System。
正常来看,这个方程是没有解的,但在数值计算领域,我们通常是计算 ![]() ,解出其中的
,解出其中的 ![]() 。比较直观的做法是求解
。比较直观的做法是求解
![]()
,但通常比较低效。其中一种常见的解法是对
![]() 进行QR分解(
进行QR分解( ![]() ),其中
),其中 ![]() 是
是 ![]() 正交矩阵(Orthonormal Matrix),
正交矩阵(Orthonormal Matrix),
如果AAT=E(E为单位矩阵,AT表示“矩阵A的转置矩阵”)或ATA=E,则n阶实矩阵A称为正交矩阵 [1] 。
![]() 是
是 ![]() 上三角矩阵(Upper Triangular Matrix),三角矩阵是方形矩阵的一种,因其非零系数的排列呈三角形状而得名。三角矩阵分上三角矩阵和下三角矩阵两种。上三角矩阵的对角线左下方的系数全部为零,下三角矩阵的对角线右上方的系数全部为零。三角矩阵可以看做是一般方阵的一种简化情形。
上三角矩阵(Upper Triangular Matrix),三角矩阵是方形矩阵的一种,因其非零系数的排列呈三角形状而得名。三角矩阵分上三角矩阵和下三角矩阵两种。上三角矩阵的对角线左下方的系数全部为零,下三角矩阵的对角线右上方的系数全部为零。三角矩阵可以看做是一般方阵的一种简化情形。
则有
![]()
参考:https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95/2522346?fr=aladdin