衍射极限、MTF与相机分辨率(1)
关于衍射极限、MTF以及像素大小的问题一直是我的一块心病。说完全不了解,又大概知道这么一回事;可真正要我来讲,却又不能严密而系统地跟别人解释清楚。仿佛就如同梦境里的一个场景,能真真切切看到它的存在,却又难以捉摸,有时跑到跟前细看,又不是那么回事。比如很简单的:
1、已知一个光学系统的F数、光波长,那它的像素大小到达一个什么水平时,算是充分利用了光学系统的分辨本领?换句话说,像素最小做到多大合适?
2、镜头设计时一般以lp/mm作为分辨率的指标来衡量MTF,那是否这个值越好,镜头就越好呢?
3、为什么1000多万像素的手机,分辨率反而不如几百万像素的相机?
这些问题,以前要我讲个究竟出来,是很困难的。最近我找了一些资料看,似乎理解比以前要透彻一些了。我今天试着讲一下(趁头脑还算清楚),等讲完了,我们回过头来,看看这几个问题的解答。
一、衍射极限与艾里斑
稍微深入玩过点摄影的都知道,一个理想的光点,通过镜头成像后,哪怕镜头没有任何像差,它也会变成一个光斑。光斑大小与F数有关,F数越小,光斑越小。而更深入一点,就得有一些光学的基础才能理解了,这是由于衍射引起的。简单说来,一个理想的物点发出的光,它的空间频谱是1,就是在各个空间频率均匀分布。而我们用镜头去成像,没办法把所有方向的光收集起来,只能收集镜头大小(严格的说,应该是入瞳大小)对应的这部分。这就不可避免造成了信息的丢失。这也就是衍射的本质。
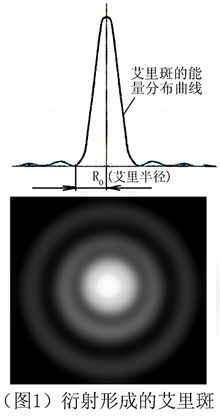
光学镜片的轮廓一般是圆形,而圆孔夫琅禾费衍射的光强分布与[J1(x)/x]^2成正比,J1(x)是一阶贝塞尔函数,x=πDsinθ/λ,J1(x)有无数个零点,前三个为3.832,7.016,10.173。光斑的一级暗环对应J1(x)的第一个零点3.832,即2πsinθ/λ=3.832,也就是sinθ=1.22λ/D时,出现了一级暗环。相应地,后续的每个零点都对应相应的二级暗环,三级暗环……,暗环和暗环之间还有亮环,但能量迅速衰减。一般我们常说的艾里斑,就是中心最亮的这个光斑,即从中心到一级暗环的这个范围。因此也就有了每提艾里斑必提到的1.22λF的这个公式,对照上面的一级暗环角度公式,我们看到/D被换成了F数,二者之间相差一个焦距f。对了,这就是半角宽度换算成焦平面上光斑半径的结果。值得一提的是,1.22λF是艾里斑半径的大小,我看很多网上的理论,都直接默认为直径大小,很不严谨。写的时候好歹先翻翻书确认一下撒。
好了,虽然我想尽量写的通俗一点,但为了交代1.22这个数字的来龙去脉,还是不可避免地扯上了数学公式。但千呼万唤,算是把艾里斑引出来了。先直观看一下艾里斑的形状(顺便说一下,我这篇博客的很多图片和数据,都引自这篇文章http://www.luminous-landscape.com/tutorials/resolution.shtml,这篇文章对我启发很大,有兴趣的可以自己看一下)
二、MTF与线对lp/mm
我们知道由于衍射和像差的存在,一个理想的光点,经过光学系统成像以后,将变成一个光斑,这是这个光学系统的点扩散函数h(t)。从空域的角度来看,一幅图像经过光学系统成像以后,由于像差和衍射的存在,肯定会退化,退化成什么样呢?就是每个点都变成了一个光斑,整幅图像就是理想图像与点扩散函数h(t)的卷积。卷积这个变换有点复杂,不太直观,于是人们就想到从频域的角度来考虑问题。因为空域的卷积对应频域的乘积。一幅图像,经过光学系统成像以后,它的频谱变化为在原来的基础上乘了一个函数H(w),H(w)是点扩散函数h(t)的傅里叶变换。H(w)就是传递函数,分为幅值和相位两部分,代表了各个频率的成分,经过光学系统以后,分别受到了不同程度的衰减和相位变化。幅值部分它影响条纹对比度的衰减,而相位部分代表条纹的移动。一般来说,我们只关注成像清晰度,这时幅值传递函数影响比相位传递函数大得多,所以我们只考虑幅值传递函数,就是我们通常说的MTF。
MTF是一个频率域的概念,代表不同频率成分对比度的衰减。就是说你去看一个单一频率的正弦条纹,理想情况下它是黑白条纹相间,反差很好;但实际上由于光学系统的像差和衍射的影响,每个点都会影响它相邻的区域,反差(对比度)会下降。条纹越密,对比度下降越厉害。而衡量这个疏密程度的单位,就是lp/mm,也就是我们常说的每毫米线对。代表每mm范围内,有几个明暗相间的正弦条纹。实际中为了方便,一般用明暗矩形条纹代替正弦条纹,一名一暗两个矩形条纹构成了一个线对。我们测试一个光学系统的MTF,就是测试对不同疏密(lp/mm为单位)的条纹的对比度衰减。为了方便比较,lp/mm通常是指像平面上的线对数。
三、离散采样、像素与线对
像质退化不仅发生在光学系统成像的过程中,还发生在将光学像变成数字化图像的过程中。现代数字设备的图像传感器无非就是CCD和CMOS两种。像素大小和间距都会造成像质的下降。整个系统的MTF是光学系统的MTF与传感器的MTF的乘积。
首先,像素大小会造成对比度的下降。因为一个像素产生的电信号是与它面积范围内光强的平均值成正比的。这就好比在原始连续光学图像上用一个均值滤波器做了一次卷积。这种均值卷积核造成的对比度下降比艾里斑的影响还有过之而无不及。
其次,像素和像素之间的间距形成了离散采样。一幅连续的光学图像,它本来有无穷多个点,现在用一些离散的像素值来表示,难免会造成信息的丢失。Shannon采样定理告诉我们,对于频率为f 的信号,我们至少要用2f的频率来采样,才能把它恢复出来。从前面的叙述,我们知道,空间频率一般是用每毫米线对数来表示的。一个线对就是一个周期,我们至少需要两个像素来采样它。因此,如果一个镜头,它最高可以分辨n lp/mm频率的条纹,那么我们必须保证每毫米有2n个像素才行,这样才能充分利用镜头的分辨能力;反过来,如果我们每mm只有n个像素,那么镜头分辨率做到n/2 lp/mm就可以了,再做高没意义,在离散采样的过程会丢失掉这些高频信息。
四、艾里斑、线对与MTF
是时候把艾里斑和MTF联系起来了。我们来看一看艾里斑对对比度的衰减能达到什么程度。
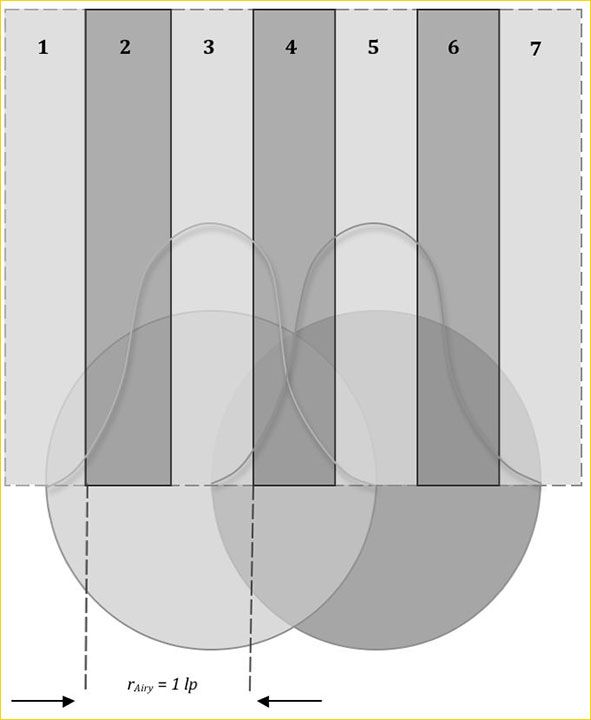
首先来看最经典的一个情形——瑞利判据。瑞利判据是说,当两个相邻的艾里斑距离为其半径时,这两个艾里斑勉强能够分辨出来。
我们看到,从一个艾里斑的中心3到另一个艾里斑的中心5,依次经历了一个从最亮到最暗再到最亮的过程。因此,一个线对(两个像素)的宽度等于艾里斑的半径大小。当然由于它们是这么密,实际上暗部和亮部没差多少,MTF非常差,只有0.09。在这个频率往上,系统是衍射受限的。哪怕没有任何像差,MTF都很差,细节几乎不可分辨。
好,我们不要太贪心,条纹太密的话MTF很差,没有意义。我们将空间频率减小一半,让一个线对宽带等于艾里斑直径的大小
可以看到条纹变宽了以后,对比度明显提高了不少(MTF约有50%左右)
频率继续减半,让一个线对宽带等于两个艾里斑直径大小
这个时候,对比度已经很好了(MTF~0.8)。可以说,在这个空间频率之下,系统已经不再是衍射受限了,影响像质的主要是光学系统的像差,只要像差控制得够好,接近理想光学系统,那么MTF可以做得很好。
至此我们可以来回答一下第一个问题。对于一个F数为2.8的镜头,假设我们用555nm的黄绿光来成像,像素大小做到多少合适呢?我们取线对宽度等于艾里斑的直径大小作为依据,此时只考虑衍射的话,MTF约有0.5,也还算可以了。一个线对对应两个像素,那么一个像素大小就相当于艾里斑的半径,也就是1.22λF,算出来约为1.9微米。如果固定传感器大小的话,那么它的像素数就是有上限的。到达一个限度,再增加像素数,就会导致像素小于1.9微米,再增加的像素已经提供不了新的信息了。具体表现,就是我们经常看手机拍的图片时会有的感觉,虽然像素很多,但只能在一个缩放比例以下去看,放大到原始大小来看,像素和像素之间是模糊的,没有细节。