基于用户历史行为数据的广告推荐模型
今天我们来讲解三篇利用用户历史行为数据建模的广告推荐模型,相比于传统的广告推荐模型,他针对用户历史行为进行了更好的建模,部分模型甚至仔细考虑了用户行为之间的时间间隔信息。
第一篇主要参考了IJCAI 2018年的paper《A Brand-level Ranking System with the Customized Attention-GRU Model》。首先来说这个广告预测推荐的场景比较少见,即从品牌的角度来对用户的行为进行预测,输入是一个长度为n的三元组序列(user, brand, timestamp),预测未来某一个时间点用户是否会购买/点击某一个brand下面的商品。整个模型以GRU为基础模型。GRU的公式如下所示:
z m = σ ( W z x m + U z s m − 1 ) z_m=\sigma (W_z x_m +U_z s_{m-1}) zm=σ(Wzxm+Uzsm−1)
r m = σ ( W r x m + U r s m − 1 ) r_m=\sigma (W_r x_m + U_rs_{m-1}) rm=σ(Wrxm+Ursm−1)
s m = z m ⨀ t a n h ( W h x m + U h ( r m ⨀ x m − 1 ) ) + ( 1 − z m ) ⨀ s m − 1 s_m=z_m \bigodot tanh(W_hx_m+U_h(r_m \bigodot x_{m-1}))+(1-z_m) \bigodot s_{m-1} sm=zm⨀tanh(Whxm+Uh(rm⨀xm−1))+(1−zm)⨀sm−1
所谓的attention方式,我感觉是作者强行把这篇paper往encoder-decoder架构上进行靠拢,即认为输入n的三元组序列就是sorce序列 ( x 1 , x 2 . . . . x n ) (x_1,x_2....x_n) (x1,x2....xn),经过输入encoder变换会生成中间结果序列 ( h 1 , h 2 , . . . . . h n ) (h_1,h_2,.....h_n) (h1,h2,.....hn),而输出就是1个单位长度的序列 y 1 y_1 y1,即对应某一个brand是否会购买,其改进的attention机制公式如下:
α 0 = A t t e n t i o n ( y 0 , h ) \alpha_0=Attention(y_{0},h) α0=Attention(y0,h)
g 0 = ∑ j = 1 L α 0 , j h j g_0=\sum_{j=1}^L \alpha_{0,j} h_j g0=∑j=1Lα0,jhj
s 0 = G R U ( y 0 , g 0 ) s_0=GRU(y_0,g_0) s0=GRU(y0,g0)
o 1 = S o f t m a x ( V s o ) o_1=Softmax(V s_o) o1=Softmax(Vso)
其中 y 0 y_0 y0就是要检测的brand的表征形式。最后模型的损失函数为log损失,即一个简单的二分类问题,即用户是否会购买目标brand。
其实到这里,整个模型已经介绍完了,但是在GRU进行encoder处理的过程中,作者对传统的GRU进行了三处改进:
1 Combining the brand features and brand embedding to better represent the brand
也就是说把特征工程得到的向量和模型自适应学习的embedding向量相加作为brand的表征形式,即 R ( b ) = M e m b e d ∗ o k + v k R(b)=M_{embed} * o_k + v_k R(b)=Membed∗ok+vk, o k o_k ok是one-hot的形式, v k v_k vk是brand的人工特征向量, M e m b e d M_{embed} Membed是brand的模型参数形式。而这个 v k v_k vk的生成挺有意思的,我这里着重讲一下,流程图如下所示:
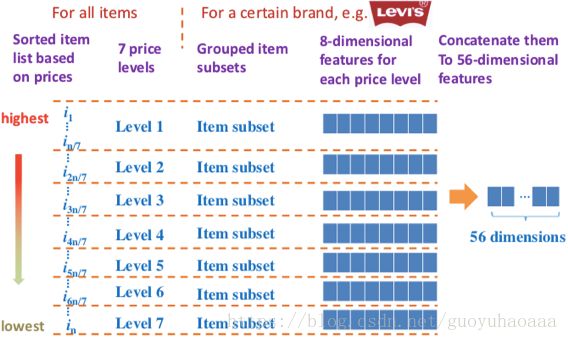
1 首先从对某个特定的类别角度对所有的item进行排序;
2 按照价格从高到低的顺序把所有的商品划分为7个level;
3 对于某一个特定的brand,其会在不同的level对应不同的商品,那么针对该brand在不同的level的item集合,会对每一个item集合进行8个维度的指标统计,这些指标如下所示:

这样在经过处理之后,每一个item会对应人工特征工程的56维数据。
2 Considering different types of actions
因为用户针对某一个brand的行为可以分为:购买或者点击两类,针对这两类行为在使用GRU进行用户行为建模的时候,会针对不同的行为进行区别对待。这这里的处理方式十分简单,就是把步骤1生成的 R ( b ) R(b) R(b)乘上一个参数矩阵,即进行空间的映射变化,方式如下:
R ( b ) = M c l i c k ∗ R ( b ) R(b)=M_{click}*R(b) R(b)=Mclick∗R(b) if b is clicked
R ( b ) = M p u r c h a s e ∗ R ( b ) R(b)=M_{purchase}*R(b) R(b)=Mpurchase∗R(b) if b is purchased
其中 M p u r c h a s e M_{purchase} Mpurchase和 M c l i c k M_{click} Mclick的维度都是 R ∈ 56 ∗ 56 R \in 56*56 R∈56∗56,这两个矩阵属于模型的参数,会随着模型一起训练。
3 Integrating the time-gate to model time intervals between actions
这一点是最有意思的,因为用户点击或者购买brand的序列会有一个timestamp信息,这部分时间间隔信息也可以进行专门的编码,即通过time-gate的方式进行引入:
T m = σ ( W t x m + σ ( Q t ∇ t m ) ) T_m=\sigma (W_t x_m +\sigma (Q_t \nabla t_m)) Tm=σ(Wtxm+σ(Qt∇tm))
∇ t m \nabla t_m ∇tm就是两个action之间的时间间隔,这里的单位是秒,最后对GRU的改变如下:
s m = z m ⨀ T m ⨀ t a n h ( W h x m + U h ( r m ⨀ x m − 1 ) ) + ( 1 − z m ) ⨀ s m − 1 s_m=z_m \bigodot T_m \bigodot tanh(W_hx_m+U_h(r_m \bigodot x_{m-1}))+(1-z_m) \bigodot s_{m-1} sm=zm⨀Tm⨀tanh(Whxm+Uh(rm⨀xm−1))+(1−zm)⨀sm−1
最后在对模型进行训练的时候,其损失函数如下:
L o s s = − ∑ i = 1 n y i l o g ( p ( R ( b ) ) ) + ( 1 − y i ) ∗ w ∗ ( 1 − p ( R ( b ) ) ) Loss = -\sum_{i=1}^n y_i log(p(R(b)))+(1-y_i)*w*(1-p(R(b))) Loss=−∑i=1nyilog(p(R(b)))+(1−yi)∗w∗(1−p(R(b)))
可以发现和一般的交叉熵不一样,在负样本那里乘了一个 w w w,这个 w w w的取值范围是 [ 0 , 1 ] [0,1] [0,1],是一个压缩系数。之所以这样做,是因为有一些正样本没有标注出来,被混在了负样本之间。
整个模型我认为还是有可以改进的地方,比方说他在建模的时候并没有考虑用户因素,即使对所有的brand进行统一建模。如果能把用户信息表征到模型之中,模型的性能也许还能提高,毕竟不同level的用户消费的brand的level也是不一样的。
第二篇参考了2018年的IJCAI的paper《Sequential Recommender System based on Hierarchical Attention Network》,他的目标是推荐场景,即根据用户的历史购买的item信息来预测用户未来会购买的item列表。整个模型结构图如下所示:

其实整个模型还是比较简单的,就是一个双层attention机制的神经网络,其实他的任务描述的还是挺有意思的,给一个用户的1到t时刻的transactions序列信息,表征为 L = S 1 , S 2 , S 3 . . . . S t L={S_1,S_2,S_3....S_t} L=S1,S2,S3....St,其中 S t S_t St代表了t时刻的用户transactions的item集合,我们需要预测该用户 S t + 1 S_{t+1} St+1时刻的交易信息。作者之所以使用two level的attention机制,是因为他综合考虑了用户的long-term和short-term信息,其中 S 1 , S 2 , . . . . S t − 1 S_1,S_2,....S_{t-1} S1,S2,....St−1可以看成是用户long-term的行为信息, S t S_t St可以看成用户short-term的行为信息。首先作者先使用attention机制对long-term行为信息进行处理,公式如下:
h 1 , j = R e l u ( W 1 v j + b 1 ) h_{1,j}=Relu(W_1 v_j+b_1) h1,j=Relu(W1vj+b1)
α j = e x p ( u T ∗ h 1 , j ) ∑ p ∈ L t − 1 u e x p ( u T ∗ h 1 , p ) \alpha_{j}=\frac{exp(u^T * h_{1,j})}{\sum_{p \in L_{t-1}^u}exp(u^T * h_{1,p})} αj=∑p∈Lt−1uexp(uT∗h1,p)exp(uT∗h1,j)
u t − 1 l o n g = ∑ j ∈ L t − 1 u α j ∗ v j u^{long}_{t-1}=\sum_{j \in L^u_{t-1} } \alpha_j * v_j ut−1long=∑j∈Lt−1uαj∗vj
当得到了目标用户long-term的表征 u t − 1 l o n g u^{long}_{t-1} ut−1long之后,把其和short-term的商品再经过一个类似的attention结构,最后得到整体的用户表征 u a i m u_{aim} uaim,接下来再把这个表征向量 u a i m u_{aim} uaim和带预测的item v j v_j vj求内积,即 R j = u a i m ∗ v j R_{j}=u_{aim} * v_j Rj=uaim∗vj,就能得到该用户对于该商品的预测信息。在进行损失函数构造的时候,该paper利用了pairwise的思想,并不是去预测特定商品的绝对分数,而是对于不同商品之间的排序信息进行预测,其公式如下所示:
a r g arg arg m i n θ − ∑ I n σ ( R i − R j ) + λ u v ∣ ∣ θ u v ∣ ∣ 2 + λ a ∣ ∣ θ a ∣ ∣ 2 min_{\theta} -\sum In\sigma(R_{i}-R_{j})+\lambda_{uv}||\theta_{uv}||^2+\lambda_{a}||\theta_a||^2 minθ−∑Inσ(Ri−Rj)+λuv∣∣θuv∣∣2+λa∣∣θa∣∣2
第三篇参考了2017年IJCAI的paper《What to Do Next: Modeling User Behaviors by Time-LSTM》,其实它比前两篇时间都早,是最早提出使用RNN系列模型来解决RS系统(推荐系统)的行为序列时间间隔不一致的问题,该问题如下所示:
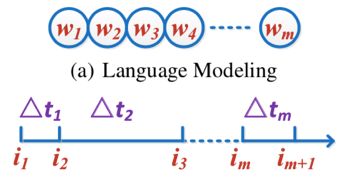
因此为了解决time interval的问题,作者在传统的LSTM的基础上增加了time gate,即既要对用户的long-term信息进行编码,又要对用户的short-term信息进行编码,综合考虑用户的长期偏好和最近的行为偏好。并提出了三种方案,首先我们来简单介绍一下基础的LSTM的公式:
i m = σ i ( x m W x i + h m − 1 W h i + w c i ⨀ c m − 1 + b i ) i_m=\sigma_i (x_m W_{xi}+h_{m-1}W_{hi}+w_{ci} \bigodot c_{m-1} + b_i) im=σi(xmWxi+hm−1Whi+wci⨀cm−1+bi)
f m = σ f ( x m W x f + h m − 1 W h f + w c f ⨀ c m − 1 + b f ) f_m=\sigma_f (x_m W_{xf}+h_{m-1}W_{hf}+w_{cf} \bigodot c_{m-1} + b_f) fm=σf(xmWxf+hm−1Whf+wcf⨀cm−1+bf)
c m = f m ⨀ c m − 1 + i m ⨀ σ c ( x m W x c + h m − 1 W h c + b c ) c_m=f_m \bigodot c_{m-1}+i_m \bigodot \sigma_c(x_mW_{xc}+h_{m-1}W_{hc}+b_c) cm=fm⨀cm−1+im⨀σc(xmWxc+hm−1Whc+bc)
o m = σ o ( x m W x o + h m − 1 W h o + w c o ⨀ c m − 1 + b o ) o_m=\sigma_o (x_m W_{xo}+h_{m-1}W_{ho}+w_{co} \bigodot c_{m-1} + b_o) om=σo(xmWxo+hm−1Who+wco⨀cm−1+bo)
h m = o m ⨀ t a n h ( c m ) h_m=o_m \bigodot tanh(c_m) hm=om⨀tanh(cm)
接下来,我们详细介绍一下三种引入了time gate的LSTM结构,其整体结构图如下所示:
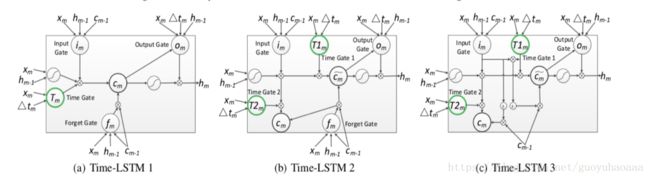
(我看这些图片比较头晕,所以就直接上公式了)
Time-LSTM 1
T m = σ t ( x m W x t + σ ( ∇ t m W t t ) + b t ) T_m = \sigma _t(x_mW_{xt}+\sigma(\nabla t_m W_{tt})+b_t) Tm=σt(xmWxt+σ(∇tmWtt)+bt)
c m = f m ⨀ c m − 1 + i m ⨀ T m ⨀ σ c ( x m W x c + h m − 1 W h c + b c ) c_m=f_m \bigodot c_{m-1}+i_m \bigodot T_m \bigodot \sigma_c(x_mW_{xc}+h_{m-1}W_{hc}+b_c) cm=fm⨀cm−1+im⨀Tm⨀σc(xmWxc+hm−1Whc+bc)
o m = σ o ( x m W x o + ∇ t m W t o + h m − 1 W h o + w c o ⨀ c m − 1 + b o ) o_m=\sigma_o (x_m W_{xo}+\nabla t_m W_{to}+h_{m-1}W_{ho}+w_{co} \bigodot c_{m-1} + b_o) om=σo(xmWxo+∇tmWto+hm−1Who+wco⨀cm−1+bo)
T m T_m Tm在其中的作用主要体现在两点:
1 一方面 T m T_m Tm可以对于输入信息进行过滤;
2 另一方面 ∇ t m \nabla t_m ∇tm首先被存储在了 T m T_m Tm之中,然后该信息会被传递到 c m c_m cm中,接下来就会被一次传递到 c m + 1 , c m + 2 . . . . c_{m+1},c_{m+2}.... cm+1,cm+2....之中,因此 ∇ t m \nabla t_m ∇tm会帮助对用户的长期兴趣进行建模。
Time-LSTM 2
在该改进的模型之中,增加了两个gate,分别是 T 1 m T1_m T1m和 T 2 m T2_m T2m,它们的计算公式如下:
T 1 m = σ t ( x m W x 1 + σ ( ∇ t m W t 1 ) + b 1 ) T1_{m} = \sigma _t(x_mW_{x1}+\sigma(\nabla t_m W_{t1})+b_1) T1m=σt(xmWx1+σ(∇tmWt1)+b1)
s . t s.t s.t W t 1 < = 0 W_{t1}<=0 Wt1<=0
T 2 m = σ t ( x m W x 2 + σ ( ∇ t m W t 2 ) + b 2 ) T2_{m} = \sigma _t(x_mW_{x2}+\sigma(\nabla t_m W_{t2})+b_2) T2m=σt(xmWx2+σ(∇tmWt2)+b2)
之所以有 W t 1 < = 0 W_{t1}<=0 Wt1<=0的限制,是因为为了保证当最近一次的 ∇ t m \nabla t_m ∇tm比较小的时候 T m T_m Tm会输出比较大的值,而当 ∇ t m \nabla t_m ∇tm比较大的时候 T m T_m Tm会输出比较小的值,也是为了把最近的 ∇ t m \nabla t_m ∇tm信息进行编码。
z m = f m ⨀ c m − 1 + i m ⨀ T 1 m ⨀ σ c ( x m W x c + h m − 1 W h c + b c ) z_m=f_m \bigodot c_{m-1}+i_m \bigodot T1_m \bigodot \sigma_c(x_mW_{xc}+h_{m-1}W_{hc}+b_c) zm=fm⨀cm−1+im⨀T1m⨀σc(xmWxc+hm−1Whc+bc)
c m = f m ⨀ c m − 1 + i m ⨀ T 2 m ⨀ σ c ( x m W x c + h m − 1 W h c + b c ) c_m=f_m \bigodot c_{m-1}+i_m \bigodot T2_m \bigodot \sigma_c(x_mW_{xc}+h_{m-1}W_{hc}+b_c) cm=fm⨀cm−1+im⨀T2m⨀σc(xmWxc+hm−1Whc+bc)
o m = σ o ( x m W x o + ∇ t m W t o + h m − 1 W h o + w c o ⨀ z m + b o ) o_m=\sigma_o (x_m W_{xo}+\nabla t_m W_{to}+h_{m-1}W_{ho}+w_{co} \bigodot z_{m} + b_o) om=σo(xmWxo+∇tmWto+hm−1Who+wco⨀zm+bo)
h m = o m ⨀ σ h ( z m ) h_m=o_m \bigodot \sigma_h(z_m) hm=om⨀σh(zm)
Time-LSTM 3
这个其实和LSTM 2是非常相似的,只不过就是把忘记门拿掉了,公式如下:
z m = ( 1 − i m ⨀ T 1 m ) ⨀ c m − 1 + i m ⨀ T 1 m ⨀ σ c ( x m W x c + h m − 1 W h c + b c ) z_m=(1-i_m \bigodot T1_m) \bigodot c_{m-1}+i_m \bigodot T1_m \bigodot \sigma_c(x_mW_{xc}+h_{m-1}W_{hc}+b_c) zm=(1−im⨀T1m)⨀cm−1+im⨀T1m⨀σc(xmWxc+hm−1Whc+bc)
c m = ( 1 − i m ) ⨀ c m − 1 + i m ⨀ T 2 m ⨀ σ c ( x m W x c + h m − 1 W h c + b c ) c_m=(1-i_m) \bigodot c_{m-1}+i_m \bigodot T2_m \bigodot \sigma_c(x_mW_{xc}+h_{m-1}W_{hc}+b_c) cm=(1−im)⨀cm−1+im⨀T2m⨀σc(xmWxc+hm−1Whc+bc)