【机器学习】手推EM算法

Andrew Wu那门《机器学习》真的是太好了，每次看都有不少新收获，今天打算重新回顾一下EM算法来着，结果看李航的《统计学习方法》发现之前的理解有不少错误，又重新开始研究，结果都不是很明白，看Andrew Wu的视频，顿时就明白了。大牛果然是大牛。

EM算法是一个非常经典的非监督学习算法。
一般手推EM算法，需要先说琴生不等式【Jensen不等式】

琴生不等式

如果一个函数是凸函数： f(x⃗ ) 的Hessian矩阵 ∇2f 是一个半正定矩阵，则其是一个凸函数。那么其满足琴生不等式：

E[f(X)]≥f(EX)

等号取到的条件

如果 ∇2f 是一个正定矩阵,则等号取到的条件是其中的 X 是一个定值,即 X 是相等的

EM算法

数理统计的基本问题就是根据样本所提供的信息，对总体的分布或者分布的数字特征作出统计推断。在EM算法中，变量并不直接是观测变量，而是含有隐含变量。如果随机变量都是可以观测的，那么直接用最大似然估计就能求出来了。但是它并不是直接可以观测的。
比如李航的《统计学习方法》中，举的那个例子，3枚硬币投出正面的概率分别为{p,q,r}，然后先投第一枚硬币，如果第一枚朝正面，则投第二枚硬币得到其值；如果反面则投第三枚硬币得到其值。现在有一个序列的观测值，问从这个观测序列中，求出{p,q,r}
因为第一枚硬币的投出的结果是不可直接观测的，所以就有了这么一个隐含的变量。
再比如混合高斯模型也是这样，并不知道每个节点的类别，所以每个节点的类别是隐含变量。【K-means也是如此】

EM算法的优化过程直观理解是如下图的，即当前节点 θn 是如下的位置 然后找到当前函数的一个下界,且这个下界是可以在 θn 节点取到的.然后再找出这个下界的最大值,其横坐标就为 θn+1
所以上面找下界的步骤是E步骤,找下界最大值求出 θn+1 的步骤是M步骤

E步骤

先定义一下以下用到的各个变量：
xi 表示观测到的结果
θ 表示问题需要求解的参数,如果是上述三硬币问题就是{p,q,r}
z 表示隐含变量,如果是上述三硬币问题,那就是第一个硬币的正反,如果是混合高斯模型则是每个节点的类别
那么我们来找下界。
最大似然函数:

l(θn)=∏i=1mP(xi|θ)=∏i=1mP(xi|θ)

因为

P(xi|θ)=∑zP(xi,z|θ)

带入上式得到

l(θn)=∏i=1m∑zP(xi,z|θ)

所以

L(θn)=∑i=1mlog∑zP(xi,z|θ)

下面就是EM算法的精髓的部分了, 变换非常有技巧

L(θn)=∑i=1mlog∑zQ(z)P(xi,z|θ)Q(z)

将其 ∑zQ(z)P(xi,z|θ)Q(z) 这部分看成一个求Q(z)分布均值的过程,则

L(θn)=∑i=1mlogE[P(xi,z|θ)Q(z)]

按照上式的琴生不等式,因为log是一个上凸函数,所以 logEX≥E[logX]

L(θn)≥∑i=1mE[logP(xi,z|θ)Q(z)]

所以 L(θn) 的下界找到了,但是如何让这个下界变成一个紧的下界呢,即

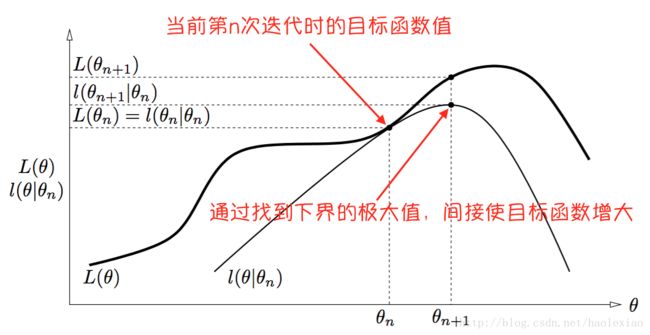
这张图中, L(θn)=l(θn|θn) 这个点能取到.
PS一般后面这个下界需要写成函数 Q(θ|θn) 不过这里写成 l(θ|θn) 这样一个函数也行吧,所以

Q(θ|θn)=∑i=1mE[logP(xi,z|θ)Q(z)]

如何保证能够取到呢,这就用到琴生不等式的性质了,即等号取到的条件是 X 为一个定值,所以

Q(z)∝P(xi,z|θ)

又因为 ∑zQ(z)=1 所以

Q(z)=P(xi,z|θ)∑zP(xi,z|θ)

而

∑zP(xi,z|θ)=P(xi|θ)

所以

Q(z)=P(xi,z|θ)P(xi|θ)

Q(z)=P(z|xi,θ)

所以E步骤就是求解 Q(z)
而一般求解 Q(z) 就是用

Q(z)=P(xi,z|θ)∑zP(xi,z|θ)

这个公式来求.
E步骤本质上相当于固定 θ 来优化 Q(z)

M步骤

上一步求解出了 Q(z) 之后,带入 Q(θ|θn) 之中得到关于 θ 的函数

Q(θ|θn)=∑i=1mE[logP(xi,z|θ)Q(z)]

Q(θ|θn)=∑i=1m∑zQ(z)logP(xi,z|θ)Q(z)

Q此时看成 θ 的函数,找出其最大值即可.
M步骤本质上相当于,固定 Q(z) 来优化 θ