吴恩达Coursera深度学习课程 deeplearning.ai (2-1) 深度学习实践--编程作业
可执行源码:https://download.csdn.net/download/haoyutiangang/10495505
初始化
一个好的初始化可以做到:
- 梯度下降的快速收敛
- 收敛到的对训练集只有较少错误的值
加载数据
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from init_utils import sigmoid, relu, compute_loss, forward_propagation, backward_propagation
from init_utils import update_parameters, predict, load_dataset, plot_decision_boundary, predict_dec
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# load image dataset: blue/red dots in circles
train_X, train_Y, test_X, test_Y = load_dataset()备用方法介绍
def sigmoid(x):
"""
Compute the sigmoid of x
Arguments:
x -- A scalar or numpy array of any size.
Return:
s -- sigmoid(x)
"""
s = 1/(1+np.exp(-x))
return s
def relu(x):
"""
Compute the relu of x
Arguments:
x -- A scalar or numpy array of any size.
Return:
s -- relu(x)
"""
s = np.maximum(0,x)
return s
def compute_loss(a3, Y):
"""
Implement the loss function
Arguments:
a3 -- post-activation, output of forward propagation
Y -- "true" labels vector, same shape as a3
Returns:
loss - value of the loss function
"""
m = Y.shape[1]
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
loss = 1./m * np.nansum(logprobs)
return loss
def forward_propagation(X, parameters):
"""
Implements the forward propagation (and computes the loss) presented in Figure 2.
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape ()
b1 -- bias vector of shape ()
W2 -- weight matrix of shape ()
b2 -- bias vector of shape ()
W3 -- weight matrix of shape ()
b3 -- bias vector of shape ()
Returns:
loss -- the loss function (vanilla logistic loss)
"""
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
z1 = np.dot(W1, X) + b1
a1 = relu(z1)
z2 = np.dot(W2, a1) + b2
a2 = relu(z2)
z3 = np.dot(W3, a2) + b3
a3 = sigmoid(z3)
cache = (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3)
return a3, cache
def backward_propagation(X, Y, cache):
"""
Implement the backward propagation presented in figure 2.
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat)
cache -- cache output from forward_propagation()
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3) = cache
dz3 = 1./m * (a3 - Y)
dW3 = np.dot(dz3, a2.T)
db3 = np.sum(dz3, axis=1, keepdims = True)
da2 = np.dot(W3.T, dz3)
dz2 = np.multiply(da2, np.int64(a2 > 0))
dW2 = np.dot(dz2, a1.T)
db2 = np.sum(dz2, axis=1, keepdims = True)
da1 = np.dot(W2.T, dz2)
dz1 = np.multiply(da1, np.int64(a1 > 0))
dW1 = np.dot(dz1, X.T)
db1 = np.sum(dz1, axis=1, keepdims = True)
gradients = {"dz3": dz3, "dW3": dW3, "db3": db3,
"da2": da2, "dz2": dz2, "dW2": dW2, "db2": db2,
"da1": da1, "dz1": dz1, "dW1": dW1, "db1": db1}
return gradients
def update_parameters(parameters, grads, learning_rate):
"""
Update parameters using gradient descent
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients, output of n_model_backward
Returns:
parameters -- python dictionary containing your updated parameters
parameters['W' + str(i)] = ...
parameters['b' + str(i)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural networks
# Update rule for each parameter
for k in range(L):
parameters["W" + str(k+1)] = parameters["W" + str(k+1)] - learning_rate * grads["dW" + str(k+1)]
parameters["b" + str(k+1)] = parameters["b" + str(k+1)] - learning_rate * grads["db" + str(k+1)]
return parameters
def predict(X, y, parameters):
"""
This function is used to predict the results of a n-layer neural network.
Arguments:
X -- data set of examples you would like to label
parameters -- parameters of the trained model
Returns:
p -- predictions for the given dataset X
"""
m = X.shape[1]
p = np.zeros((1,m), dtype = np.int)
# Forward propagation
a3, caches = forward_propagation(X, parameters)
# convert probas to 0/1 predictions
for i in range(0, a3.shape[1]):
if a3[0,i] > 0.5:
p[0,i] = 1
else:
p[0,i] = 0
# print results
print("Accuracy: " + str(np.mean((p[0,:] == y[0,:]))))
return p
def load_dataset():
np.random.seed(1)
train_X, train_Y = sklearn.datasets.make_circles(n_samples=300, noise=.05)
np.random.seed(2)
test_X, test_Y = sklearn.datasets.make_circles(n_samples=100, noise=.05)
# Visualize the data
plt.scatter(train_X[:, 0], train_X[:, 1], c=train_Y, s=40, cmap=plt.cm.Spectral);
train_X = train_X.T
train_Y = train_Y.reshape((1, train_Y.shape[0]))
test_X = test_X.T
test_Y = test_Y.reshape((1, test_Y.shape[0]))
return train_X, train_Y, test_X, test_Y
def plot_decision_boundary(model, X, y):
# Set min and max values and give it some padding
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)
plt.show()
def predict_dec(parameters, X):
"""
Used for plotting decision boundary.
Arguments:
parameters -- python dictionary containing your parameters
X -- input data of size (m, K)
Returns
predictions -- vector of predictions of our model (red: 0 / blue: 1)
"""
# Predict using forward propagation and a classification threshold of 0.5
a3, cache = forward_propagation(X, parameters)
predictions = (a3>0.5)
return predictions1 神经网络模型
我们将用一个3-layer神经网络对上文散点图进行分类。
1.2 初始化方法
- 零值初始化:initialization = “zeros”
- 随机初始化:initialization = “random”
- He 初始化:initialization = “random” (按照He的论文进行的随机初始化)
1.3 三层神经网络模型
def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he"):
"""
Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (2, number of examples)
Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples)
learning_rate -- learning rate for gradient descent
num_iterations -- number of iterations to run gradient descent
print_cost -- if True, print the cost every 1000 iterations
initialization -- flag to choose which initialization to use ("zeros","random" or "he")
Returns:
parameters -- parameters learnt by the model
"""
grads = {}
costs = [] # to keep track of the loss
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 10, 5, 1]
# Initialize parameters dictionary.
if initialization == "zeros":
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == "random":
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
a3, cache = forward_propagation(X, parameters)
# Loss
cost = compute_loss(a3, Y)
# Backward propagation.
grads = backward_propagation(X, Y, cache)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 1000 iterations
if print_cost and i % 1000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
costs.append(cost)
# plot the loss
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters2 零值初始化
初始化(W1,b1)… (Wl,b,)
# GRADED FUNCTION: initialize_parameters_zeros
def initialize_parameters_zeros(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
parameters = {}
L = len(layers_dims) # number of layers in the network
for l in range(1, L):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.zeros((layers_dims[l],layers_dims[l-1]))
parameters['b' + str(l)] = np.zeros((layers_dims[l],1))
### END CODE HERE ###
return
parameters = initialize_parameters_zeros([3,2,1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))试一试
parameters = initialize_parameters_zeros([3,2,1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
# On the train set:
# Accuracy: 0.5
# On the test set:
# Accuracy: 0.5准确率一半,还不如猜呢,并且随着迭代次数增加,cost并没有任何变化。
plt.title("Model with Zeros initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)结论
零值初始化无法打破对称性,导致每个神经元学习同样的内容,相当于只有一层,和线性逻辑回归没什么区别。
3 随机初始化(大值初始化)
# GRADED FUNCTION: initialize_parameters_random
def initialize_parameters_random(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
np.random.seed(3) # This seed makes sure your "random" numbers will be the as ours
parameters = {}
L = len(layers_dims) # integer representing the number of layers
for l in range(1, L):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1])*10
parameters['b' + str(l)] = np.zeros((layers_dims[l],1))
### END CODE HERE ###
return parameters
parameters = initialize_parameters_random([3, 2, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))试一试
parameters = model(train_X, train_Y, initialization = "random")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
# On the train set:
# Accuracy: 0.83
# On the test set:
# Accuracy: 0.86plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)结论
- 用大值随机初始化时开始cost很大,逐步缩小,但下降缓慢
- 不好的初始化会导致梯度消失或梯度爆炸,也拖慢了算法优化的速度
看来小值初始化会表现的更好,但是小值是多小呢?
4 He 初始化
- He 初始化Wl:sqrt(2./layers_dims[l-1])
- Xavier 初始化Wl:sqrt(1./layers_dims[l-1])
# GRADED FUNCTION: initialize_parameters_he
def initialize_parameters_he(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims) - 1 # integer representing the number of layers
for l in range(1, L + 1):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1])*np.sqrt(2./layers_dims[l-1])
parameters['b' + str(l)] = np.zeros((layers_dims[l],1))
### END CODE HERE ###
return parameters
parameters = initialize_parameters_he([2, 4, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))试一试
parameters = model(train_X, train_Y, initialization = "he")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)总结
很明显,在不多的循环下,分类效果就已经很好了。
5 各种初始化的结论
| Model | Train accuracy | Problem/Comment |
|---|---|---|
| 3-layer NN 零值初始化 | 50% | 无法打破对称性 |
| 3-layer NN with large random initialization | 83% | 权重太大 |
| 3-layer NN with He initialization | 99% | 推荐的算法 |
正则化
1 导包
# import packages
import numpy as np
import matplotlib.pyplot as plt
from reg_utils import sigmoid, relu, plot_decision_boundary, initialize_parameters, load_2D_dataset, predict_dec
from reg_utils import compute_cost, predict, forward_propagation, backward_propagation, update_parameters
import sklearn
import sklearn.datasets
import scipy.io
from testCases import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'有用的方法
def initialize_parameters(layer_dims):
"""
Arguments:
layer_dims -- python array (list) containing the dimensions of each layer in our network
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
b1 -- bias vector of shape (layer_dims[l], 1)
Wl -- weight matrix of shape (layer_dims[l-1], layer_dims[l])
bl -- bias vector of shape (1, layer_dims[l])
Tips:
- For example: the layer_dims for the "Planar Data classification model" would have been [2,2,1].
This means W1's shape was (2,2), b1 was (1,2), W2 was (2,1) and b2 was (1,1). Now you have to generalize it!
- In the for loop, use parameters['W' + str(l)] to access Wl, where l is the iterative integer.
"""
np.random.seed(3)
parameters = {}
L = len(layer_dims) # number of layers in the network
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) / np.sqrt(layer_dims[l-1])
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
assert(parameters['W' + str(l)].shape == layer_dims[l], layer_dims[l-1])
assert(parameters['W' + str(l)].shape == layer_dims[l], 1)
return parameters
def compute_cost(a3, Y):
"""
Implement the cost function
Arguments:
a3 -- post-activation, output of forward propagation
Y -- "true" labels vector, same shape as a3
Returns:
cost - value of the cost function
"""
m = Y.shape[1]
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
cost = 1./m * np.nansum(logprobs)
return cost
def load_2D_dataset():
data = scipy.io.loadmat('datasets/data.mat')
train_X = data['X'].T
train_Y = data['y'].T
test_X = data['Xval'].T
test_Y = data['yval'].T
plt.scatter(train_X[0, :], train_X[1, :], c=train_Y, s=40, cmap=plt.cm.Spectral);
return train_X, train_Y, test_X, test_Y问题描述
你被法国足球俱乐部聘为 AI 专家,他们想让你推荐守门员应把球踢到什么位置以便其它法国队员可以用头部击球。

下面给出过去十场比赛的二维数据集。
train_X, train_Y, test_X, test_Y = load_2D_dataset()图中每个点对应了守门员发球到不同位置后其它球员的击球情况。
- 蓝点:法国球员击球
- 红点:其它球员击球
目标
利用深度学习模型找到守门员应该把球踢往哪些位置。
数据集分析
从数据集上看,数据有一些噪音,不过大体可以看出可以用一条斜对角线分为左上蓝点去和右下红点区。
分别尝试非正则化模型和正则化模型,最后选择用哪种模型解决该问题。
1 非正则化模型
你可以使用如下已经实现好的模型。该模型也可以用于:
- 正则化模型:只需将参数 lambd 设置为非0值
- dropout 模型:只需将参数 keep_prob 设置为小于1的数
首先尝试没有正则化的模型,然后再实现其他两种模型:
- L2 正则化:实现方法“compute_cost_with_regularization()” 和 “backward_propagation_with_regularization()”
- Dropout: 实现方法“forward_propagation_with_dropout()” 和 “backward_propagation_with_dropout()”
def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
"""
Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (output size, number of examples)
learning_rate -- learning rate of the optimization
num_iterations -- number of iterations of the optimization loop
print_cost -- If True, print the cost every 10000 iterations
lambd -- regularization hyperparameter, scalar
keep_prob - probability of keeping a neuron active during drop-out, scalar.
Returns:
parameters -- parameters learned by the model. They can then be used to predict.
"""
grads = {}
costs = [] # to keep track of the cost
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 20, 3, 1]
# Initialize parameters dictionary.
parameters = initialize_parameters(layers_dims)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
if keep_prob == 1:
a3, cache = forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# Cost function
if lambd == 0:
cost = compute_cost(a3, Y)
else:
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# Backward propagation.
assert(lambd==0 or keep_prob==1) # it is possible to use both L2 regularization and dropout,
# but this assignment will only explore one at a time
if lambd == 0 and keep_prob == 1:
grads = backward_propagation(X, Y, cache)
elif lambd != 0:
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 10000 iterations
if print_cost and i % 10000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
if print_cost and i % 1000 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters训练非正则化模型
parameters = model(train_X, train_Y)
print ("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
Cost after iteration 0: 0.6557412523481002
Cost after iteration 10000: 0.16329987525724216
Cost after iteration 20000: 0.13851642423255986On the training set:
Accuracy: 0.947867298578
On the test set:
Accuracy: 0.915训练集准确率94.8%,测试集准确率91.5%。
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)结论
从图上看,训练集明显有点过拟合了,适应了噪点。
下面我们看看降低过拟合的两种技术。
2 L2 正则化
损失函数:
- 非正则化
- 正则化
Jregularized=−1m∑i=1m(y(i)log(a[l](i))+(1−y(i))log(1−a[l](i)))+1mlambda2∑l∑k∑jW[l]2kj J r e g u l a r i z e d = − 1 m ∑ i = 1 m ( y ( i ) l o g ( a [ l ] ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − a [ l ] ( i ) ) ) + 1 m l a m b d a 2 ∑ l ∑ k ∑ j W k j [ l ] 2
实现正则化损失函数:compute_cost_with_regularization()
注意:矩阵平方的加和相乘可以使用:np.sum(np.square(Wl))
# GRADED FUNCTION: compute_cost_with_regularization
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
Implement the cost function with L2 regularization. See formula (2) above.
Arguments:
A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
parameters -- python dictionary containing parameters of the model
Returns:
cost - value of the regularized loss function (formula (2))
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost
### START CODE HERE ### (approx. 1 line)
L2_regularization_cost = (1./m*lambd/2)*(np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))
### END CODER HERE ###
cost = cross_entropy_cost + L2_regularization_cost
return cost
A3, Y_assess, parameters = compute_cost_with_regularization_test_case()
print("cost = " + str(compute_cost_with_regularization(A3, Y_assess, parameters, lambd = 0.1)))
# cost = 1.78648594516损失函数变了,那么反向传播函数也需要变化,实现:backward_propagation_with_regularization()
注意:正则化部分梯度的计算
# GRADED FUNCTION: backward_propagation_with_regularization
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
Implements the backward propagation of our baseline model to which we added an L2 regularization.
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation()
lambd -- regularization hyperparameter, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
### START CODE HERE ### (approx. 1 line)
dW3 = 1./m * np.dot(dZ3, A2.T) + lambd/m * W3
### END CODE HERE ###
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
### START CODE HERE ### (approx. 1 line)
dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m * W2
### END CODE HERE ###
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
### START CODE HERE ### (approx. 1 line)
dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m * W1
### END CODE HERE ###
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
X_assess, Y_assess, cache = backward_propagation_with_regularization_test_case()
grads = backward_propagation_with_regularization(X_assess, Y_assess, cache, lambd = 0.7)
print ("dW1 = "+ str(grads["dW1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("dW3 = "+ str(grads["dW3"]))
# dW1 = [[-0.25604646 0.12298827 -0.28297129]
# [-0.17706303 0.34536094 -0.4410571 ]]
# dW2 = [[ 0.79276486 0.85133918]
# [-0.0957219 -0.01720463]
# [-0.13100772 -0.03750433]]
# dW3 = [[-1.77691347 -0.11832879 -0.09397446]]设置 lambda = 0.7 训练模型
parameters = model(train_X, train_Y, lambd = 0.7)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
# Cost after iteration 0: 0.6974484493131264
# Cost after iteration 10000: 0.2684918873282239
# Cost after iteration 20000: 0.2680916337127301
#
#
# On the train set:
# Accuracy: 0.938388625592
# On the test set:
# Accuracy: 0.93测试集准确率提升到了93%,你拯救了法国足球队。
现在不再过拟合了。
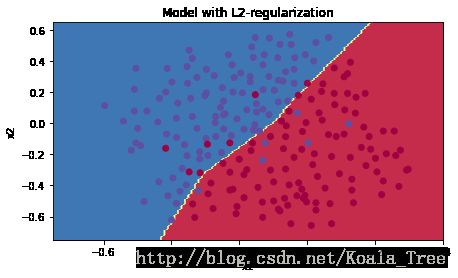
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)- 超参数 lambda 可以用于训练集和交叉验证集
- L2 正则化模型可以使边界更加平滑。如果 lambda 太大,可能会导致太过于平滑以至于导致高偏差从而导致过拟合
总结
L2 正则化假定权重小的模型比权重大的模型更加简单,加上正则化后权重更小。随着输入的变化,使输出的变化更慢更平缓。
3 Dropout
Dropout 是深度学习广泛使用的一种正则化方法。
Dropout 在每次循环中都随机关闭一些神经元
当关闭一些神经元时,其实改变了模型。每次都用一个随机剩余的子神经元来训练模型,使模型的输出对个别神经元的依赖减小,因为任何神经元在任何一次循环过程中都有可能被关闭。
3.1 dropout 前向传播
dropout 不要用在输入层和输出层,只需用到各个隐藏层即可。
- D 和 A 同纬度,表示 A 中各个输入是否消失
- 如果随机数小于门槛值则 d为0,大于门槛值则为1
- D*A 作为新的 A
- A/keep_prob 作为新的 A,这样保证 dropout 后矩阵的值大体不变,也就使 cost 函数的值大体不变。
# GRADED FUNCTION: forward_propagation_with_dropout
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
Arguments:
X -- input dataset, of shape (2, number of examples)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (20, 2)
b1 -- bias vector of shape (20, 1)
W2 -- weight matrix of shape (3, 20)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
A3 -- last activation value, output of the forward propagation, of shape (1,1)
cache -- tuple, information stored for computing the backward propagation
"""
np.random.seed(1)
# retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
### START CODE HERE ### (approx. 4 lines) # Steps 1-4 below correspond to the Steps 1-4 described above.
D1 = np.random.rand(A1.shape[0],A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = D1 < keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = A1 * D1 # Step 3: shut down some neurons of A1
A1 = A1 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
### END CODE HERE ###
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
### START CODE HERE ### (approx. 4 lines)
D2 = np.random.rand(A2.shape[0],A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...)
D2 = D2 < keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
A2 = A2 * D2 # Step 3: shut down some neurons of A2
A2 = A2 / keep_prob # Step 4: scale the value of neurons that haven't been shut down
### END CODE HERE ###
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
X_assess, parameters = forward_propagation_with_dropout_test_case()
A3, cache = forward_propagation_with_dropout(X_assess, parameters, keep_prob = 0.7)
print ("A3 = " + str(A3))
# A3 = [[ 0.36974721 0.00305176 0.04565099 0.49683389 0.36974721]]3.2 dropout 反向传播
- 反向传播时关闭同样的神经元,dA*D 作为新的 dA
- dA/keep_prob 作为新的 dA
# GRADED FUNCTION: backward_propagation_with_dropout
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
Implements the backward propagation of our baseline model to which we added dropout.
Arguments:
X -- input dataset, of shape (2, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation_with_dropout()
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
### START CODE HERE ### (≈ 2 lines of code)
dA2 = dA2 * D2 # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 = dA2 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
### END CODE HERE ###
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
### START CODE HERE ### (≈ 2 lines of code)
dA1 = dA1 * D1 # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 = dA1 / keep_prob # Step 2: Scale the value of neurons that haven't been shut down
### END CODE HERE ###
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
X_assess, Y_assess, cache = backward_propagation_with_dropout_test_case()
gradients = backward_propagation_with_dropout(X_assess, Y_assess, cache, keep_prob = 0.8)
print ("dA1 = " + str(gradients["dA1"]))
print ("dA2 = " + str(gradients["dA2"]))
# dA1 = [[ 0.36544439 0. -0.00188233 0. # -0.17408748]
# [ 0.65515713 0. -0.00337459 0. -0. ]]
# dA2 = [[ 0.58180856 0. -0.00299679 0. # -0.27715731]
# [ 0. 0.53159854 -0. 0.53159854 -0.34089673]
# [ 0. 0. -0.00292733 0. -0. ]]
# 设置 keep_prob 为0.86 训练模型
parameters = model(train_X, train_Y, keep_prob = 0.86, learning_rate = 0.3)
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)
# Cost after iteration 0: 0.6543912405149825
# Cost after iteration 10000: 0.06101698657490559
# Cost after iteration 20000: 0.060582435798513114
#
# On the train set:
# Accuracy: 0.928909952607
# On the test set:
# Accuracy: 0.95dropout 效果非常好,准确率提升到了95%,模型在训练集没有过拟合,测试集也表现良好,法国足球队将会永远感激你。
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)总结
- Dropout 是一种正则化技术(用于消除过拟合)
- Dropout 只需用于训练集,不要用于测试集。
- Dropout 只用于隐藏层,不要用于输入层和输出层
- Dropout 需要同时用于前向传播和反向传播
- 训练时,前向传播的 A 和 反向传播的 dA 都需要除以 keep_prob,保证激活函数和损失函数可以得到期待的值。
4 结论
| 模型 | 训练集准确率 | 测试集准确率 |
|---|---|---|
| 3-layer NN 没有正则化 | 95% | 91.5% |
| 3-layer NN L2 正则化 | 94% | 93% |
| 3-layer NN Dropout | 93% | 95% |
注意到正则化损害了训练集的性能,因为它限制了神经网络拟合训练集数据的能力。不过最终给出了更好的测试集准确率,对我们的系统是有帮助的。
- 正则化可以帮助消除过拟合
- 正则化其实是使权重更小,变化更缓慢
- L2 正则化和 Dropout 是两种非常有效的正则化技术。
第三部分:梯度检验
导包
# Packages
import numpy as np
from testCases import *
from gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector有用的方法
def dictionary_to_vector(parameters):
"""
Roll all our parameters dictionary into a single vector satisfying our specific required shape.
"""
keys = []
count = 0
for key in ["W1", "b1", "W2", "b2", "W3", "b3"]:
# flatten parameter
new_vector = np.reshape(parameters[key], (-1,1))
keys = keys + [key]*new_vector.shape[0]
if count == 0:
theta = new_vector
else:
theta = np.concatenate((theta, new_vector), axis=0)
count = count + 1
return theta, keys
def vector_to_dictionary(theta):
"""
Unroll all our parameters dictionary from a single vector satisfying our specific required shape.
"""
parameters = {}
parameters["W1"] = theta[:20].reshape((5,4))
parameters["b1"] = theta[20:25].reshape((5,1))
parameters["W2"] = theta[25:40].reshape((3,5))
parameters["b2"] = theta[40:43].reshape((3,1))
parameters["W3"] = theta[43:46].reshape((1,3))
parameters["b3"] = theta[46:47].reshape((1,1))
return parameters
def gradients_to_vector(gradients):
"""
Roll all our gradients dictionary into a single vector satisfying our specific required shape.
"""
count = 0
for key in ["dW1", "db1", "dW2", "db2", "dW3", "db3"]:
# flatten parameter
new_vector = np.reshape(gradients[key], (-1,1))
if count == 0:
theta = new_vector
else:
theta = np.concatenate((theta, new_vector), axis=0)
count = count + 1
return theta1 梯度检验的原理
- 前向传播很好计算,但是后向传播涉及到求导,很容易发生错误。
- 梯度检验用前向传播结合求导原理去验证求解导数的正确性。
2 1-维梯度检验
前向传播求 J
# GRADED FUNCTION: forward_propagation
def forward_propagation(x, theta):
"""
Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x)
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
J -- the value of function J, computed using the formula J(theta) = theta * x
"""
### START CODE HERE ### (approx. 1 line)
J = theta * x
### END CODE HERE ###
return J
x, theta = 2, 4
J = forward_propagation(x, theta)
print ("J = " + str(J))
# J = 8反向传播求导 grad
# GRADED FUNCTION: backward_propagation
def backward_propagation(x, theta):
"""
Computes the derivative of J with respect to theta (see Figure 1).
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
dtheta -- the gradient of the cost with respect to theta
"""
### START CODE HERE ### (approx. 1 line)
dtheta = x
### END CODE HERE ###
return dtheta
x, theta = 2, 4
dtheta = backward_propagation(x, theta)
print ("dtheta = " + str(dtheta))
# dtheta = 2梯度检验
- 反向传播求导结果为grad
- 计算gradapprox
θ+=θ+εθ−=θ−εJ+=J(θ+)J−=J(θ−)gradapprox=J+−J−2ε θ + = θ + ε θ − = θ − ε J + = J ( θ + ) J − = J ( θ − ) g r a d a p p r o x = J + − J − 2 ε - 计算gradapprox 和 grad 的相对距离
- 计算分子
- 计算分母
- 相除
- 如果值小于10^-7, 可以认为梯度正确,否则可能存在错误。
difference=||grad−gradapprox||2||grad||2+||gradapprox||2 d i f f e r e n c e = | | g r a d − g r a d a p p r o x | | 2 | | g r a d | | 2 + | | g r a d a p p r o x | | 2
# GRADED FUNCTION: gradient_check
def gradient_check(x, theta, epsilon = 1e-7):
"""
Implement the backward propagation presented in Figure 1.
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
# Compute gradapprox using left side of formula (1). epsilon is small enough, you don't need to worry about the limit.
### START CODE HERE ### (approx. 5 lines)
thetaplus = theta + epsilon # Step 1
thetaminus = theta - epsilon # Step 2
J_plus = forward_propagation(x, thetaplus) # Step 3
J_minus = forward_propagation(x, thetaminus) # Step 4
gradapprox = (J_plus - J_minus) / (2 * epsilon) # Step 5
### END CODE HERE ###
# Check if gradapprox is close enough to the output of backward_propagation()
### START CODE HERE ### (approx. 1 line)
grad = backward_propagation(x, theta)
### END CODE HERE ###
### START CODE HERE ### (approx. 1 line)
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
### END CODE HERE ###
if difference < 1e-7:
print ("The gradient is correct!")
else:
print ("The gradient is wrong!")
return difference
x, theta = 2, 4
difference = gradient_check(x, theta)
print("difference = " + str(difference))
# The gradient is correct!
# difference = 2.91933588329e-103 N-维 梯度检验
LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
前向传播
def forward_propagation_n(X, Y, parameters):
"""
Implements the forward propagation (and computes the cost) presented in Figure 3.
Arguments:
X -- training set for m examples
Y -- labels for m examples
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (5, 4)
b1 -- bias vector of shape (5, 1)
W2 -- weight matrix of shape (3, 5)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
Returns:
cost -- the cost function (logistic cost for one example)
"""
# retrieve parameters
m = X.shape[1]
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
# Cost
logprobs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y)
cost = 1./m * np.sum(logprobs)
cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
return cost, cache反向传播
def backward_propagation_n(X, Y, cache):
"""
Implement the backward propagation presented in figure 2.
Arguments:
X -- input datapoint, of shape (input size, 1)
Y -- true "label"
cache -- cache output from forward_propagation_n()
Returns:
gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables.
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
"dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients梯度检验
N-维模型,参数存于dictionary中,我们需要变成参数向量组成的矩阵
- dictionary_to_vector()
- vector_to_dictionary
实现 gradient_check_n()
对每一个参数 i:
- 计算J_plus[i]:
- 计算J_minus[i]:
- 计算gradapprox[i]
# GRADED FUNCTION: gradient_check_n
def gradient_check_n(parameters, gradients, X, Y, epsilon = 1e-7):
"""
Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
Arguments:
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters.
x -- input datapoint, of shape (input size, 1)
y -- true "label"
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
# Set-up variables
parameters_values, _ = dictionary_to_vector(parameters)
grad = gradients_to_vector(gradients)
num_parameters = parameters_values.shape[0]
J_plus = np.zeros((num_parameters, 1))
J_minus = np.zeros((num_parameters, 1))
gradapprox = np.zeros((num_parameters, 1))
# Compute gradapprox
for i in range(num_parameters):
# Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".
# "_" is used because the function you have to outputs two parameters but we only care about the first one
### START CODE HERE ### (approx. 3 lines)
thetaplus = np.copy(parameters_values) # Step 1
thetaplus[i][0] = thetaplus[i][0] + epsilon # Step 2
J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaplus)) # Step 3
### END CODE HERE ###
# Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".
### START CODE HERE ### (approx. 3 lines)
thetaminus = np.copy(parameters_values) # Step 1
thetaminus[i][0] = thetaminus[i][0] - epsilon # Step 2
J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus)) # Step 3
### END CODE HERE ###
# Compute gradapprox[i]
### START CODE HERE ### (approx. 1 line)
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2.* epsilon)
### END CODE HERE ###
# Compare gradapprox to backward propagation gradients by computing difference.
### START CODE HERE ### (approx. 1 line)
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
### END CODE HERE ###
if difference > 1e-7:
print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
else:
print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
return difference
X, Y, parameters = gradient_check_n_test_case()
cost, cache = forward_propagation_n(X, Y, parameters)
gradients = backward_propagation_n(X, Y, cache)
difference = gradient_check_n(parameters, gradients, X, Y)
# Your backward propagation works perfectly fine! difference = 0.285093156781差异太大,有错误(检查dW2 和 db1)改正错误并重新运行程序
注意
- 梯度检验速度很慢,不要在训练集每次循环中使用,使用几次即可
- 不能用于dropout模型,使用时先关闭dropout,验证后再打开