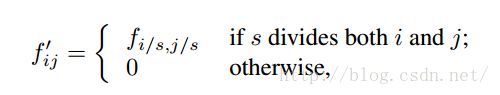论文笔记《Fully Convolutional Networks for Semantic Segmentation》

【论文信息】

《Fully Convolutional Networks for Semantic Segmentation》

CVPR 2015 best paper

key word: pixel level, fully supervised, CNN

【方法简介】

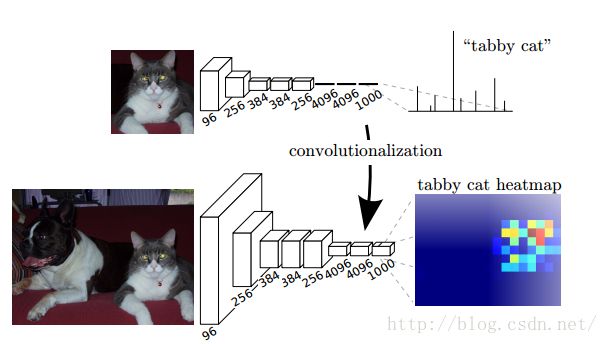
主要思路是把CNN改为FCN，输入一幅图像后直接在输出端得到dense prediction，也就是每个像素所属的class，从而得到一个end-to-end的方法来实现image  semantic segmentation。    

 我们已经有一个CNN模型，首先要把CNN的全连接层看成是卷积层，卷积模板大小就是输入的特征map的大小，也就是说把全连接网络看成是对整张输入map做卷积，全连接层分别有4096个6*6的卷积核，4096个1*1的卷积核，1000个1*1的卷积核，如下图：

接下来就要对这1000个1*1卷积核的输出，做upsampling，得到1000个原图大小（如32*32）的输出，这些输出合并后，得到上图所示的heatmap。

【细节记录】

------------2016.11.4更新---------

fcn的输入图片为什么可以是任意大小呢？

首先，我们来看传统CNN为什么需要固定输入图片大小。

对于CNN，一幅输入图片在经过卷积和pooling层时，这些层是不care图片大小的。比如对于一个卷积层，outputsize = (inputsize - kernelsize) / stride + 1，它并不关心inputsize多大，对于一个inputsize大小的输入feature map，滑窗卷积，输出outputsize大小的feature map即可。pooling层同理。等要进入全连接层时，feature map（假设大小为n×n）要拉成一条向量，而向量中每个元素（共n^2个）作为一个结点都要与下一个层的所有结点（假设4096个）全连接，这里的权值个数是4096 × n^2，而我们知道神经网络结构一旦确定，它的权值个数都是固定的，所以这个n不能变化，n是conv5的outputsize，所以层层向回看，每个outputsize都要固定，那每个inputsize都要固定，因此输入图片大小要固定。

所以可以得出结论，一个确定的CNN网络结构之所以要固定输入图片大小，是因为全连接层权值数固定，而该权值数和feature map大小有关。

接着，我们来看FCN。FCN在CNN的基础上把1000个结点的全连接层改为含有1000个1×1卷积核的卷积层，经过这一层，还是得到二维的feature map，同样我们也不关心这个feature map大小。

到了反卷积层，注意，反卷积层也是卷积层，不关心input大小，滑窗卷积后输出output。

配个动图简单理解一下：下图中蓝色是反卷积层的input，绿色是反卷积层的output。

kernel size = 3, stride = 1的反卷积，input是2×2, output是4×4

kernel size = 3, stride = 2的反卷积，input是3×3, output是5×5：

最后，问题来了，怎么使反卷积的output大小和输入图片大小一致，从而得到pixel level prediction。

我们知道，FCN里面全部都是卷积层（pooling也看成卷积），卷积层不关心input的大小，inputsize和outputsize之间存在线性关系。假设图片输入为n×n大小，第一个卷积层输出map就为conv1_out.size=(n-kernelsize)/stride + 1, 记做conv1_out.size = f(n), 依次类推，conv5_out.size = f(conv5_in.size) = f(... f(n)), 反卷积是要使n = f‘(conv5_out.size)成立，要确定f’，就需要设置deconvolution层的kernelsize，stride，padding，计算方法如下：

layer {
 name: "upsample", type: "Deconvolution"
 bottom: "{{bottom_name}}" top: "{{top_name}}"
 convolution_param {
 kernel_size: {{2 * factor - factor % 2}} stride: {{factor}}
 num_output: {{C}} group: {{C}}
 pad: {{ceil((factor - 1) / 2.)}}
 weight_filler: { type: "bilinear" } bias_term: false
 }
 param { lr_mult: 0 decay_mult: 0 }
}

其中factor是指反卷积之前的所有卷积pooling层的累积采样步长，卷积层使feature map变小，是因为stride，卷积操作造成的影响一般通过padding来消除，因此，累积采样步长factor就等于反卷积之前所有层的stride的乘积。参看FCN-alexnet的结构

-----------------------------------------------

dense prediction

这里通过upsampling得到dense prediction，作者研究过3种方案：

1，shift-and-stitch：设原图与FCN所得输出图之间的降采样因子是f，那么对于原图的每个f*f的区域（不重叠），“shift the input x pixels to the right and y pixels down for every (x,y) ,0 < x,y < f." 把这个f*f区域对应的output作为此时区域中心点像素对应的output，这样就对每个f*f的区域得到了f^2个output，也就是每个像素都能对应一个output，所以成为了dense prediction。

2，filter rarefaction：就是放大CNN网络中的subsampling层的filter的尺寸，得到新的filter：

其中s是subsampling的滑动步长，这个新filter的滑动步长要设为1，这样的话，subsampling就没有缩小图像尺寸，最后可以得到dense prediction。

以上两种方法作者都没有采用，主要是因为这两种方法都是trad-off的，原因是：

对于第二种方法， 下采样的功能被减弱，使得更细节的信息能被filter看到，但是receptive fileds会相对变小，可能会损失全局信息，且会对卷积层引入更多运算。

对于第一种方法，虽然receptive fileds没有变小，但是由于原图被划分成f*f的区域输入网络，使得filters无法感受更精细的信息。

3，这里upsampling的操作可以看成是反卷积(deconvolutional)，卷积运算的参数和CNN的参数一样是在训练FCN模型的过程中通过bp算法学习得到。

fusion prediction

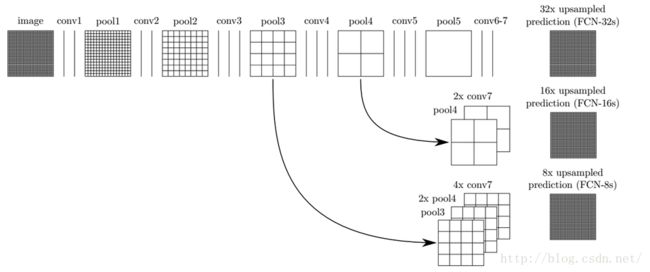
以上是对CNN的结果做处理，得到了dense prediction，而作者在试验中发现，得到的分割结果比较粗糙，所以考虑加入更多前层的细节信息，也就是把倒数第几层的输出和最后的输出做一个fusion，实际上也就是加和：

这样就得到第二行和第三行的结果，实验表明，这样的分割结果更细致更准确。在逐层fusion的过程中，做到第三行再往下，结果又会变差，所以作者做到这里就停了。可以看到如上三行的对应的结果：

【实验设计】

1，对比3种性能较好的几种CNN：AlexNet, VGG16, GoogLeNet进行实验，选择VGG16

2，对比FCN-32s-fixed, FCN-32s, FCN-16s, FCN-8s，证明最好的dense prediction组合是8s

3，FCN-8s和state-of-the-art对比是最优的，R-CNN, SDS.   FCN-16s

4，FCN-16s和现有的一些工作对比，是最优的

5，FCN-32s和FCN-16s在RGB-D和HHA的图像数据集上，优于state-of-the-art

【总结】

优点

1，训练一个end-to-end的FCN模型，利用卷积神经网络的很强的学习能力，得到较准确的结果，以前的基于CNN的方法都是要对输入或者输出做一些处理，才能得到最终结果。

2，直接使用现有的CNN网络，如AlexNet, VGG16, GoogLeNet，只需在末尾加上upsampling，参数的学习还是利用CNN本身的反向传播原理，"whole image training is effective and efficient."

3，不限制输入图片的尺寸，不要求图片集中所有图片都是同样尺寸，只需在最后upsampling时按原图被subsampling的比例缩放回来，最后都会输出一张与原图大小一致的dense prediction map。

缺陷

根据论文的conclusion部分所示的实验输出sample如下图：

可以直观地看出，本文方法和Groud truth相比，容易丢失较小的目标，比如第一幅图片中的汽车，和第二幅图片中的观众人群，如果要改进的话，这一点上应该是有一些提升空间的。