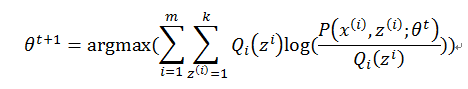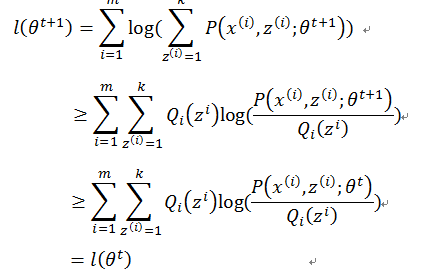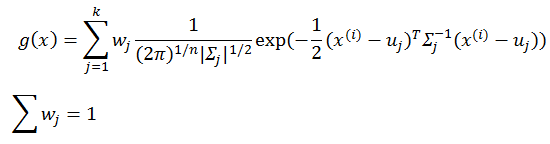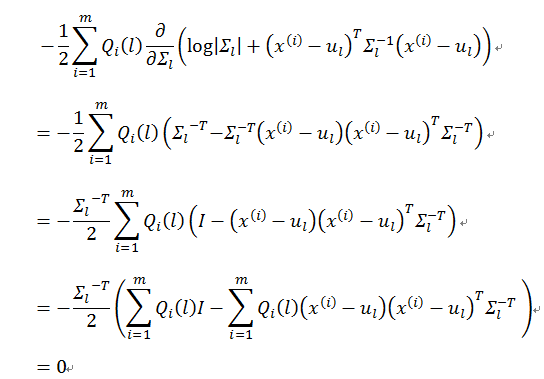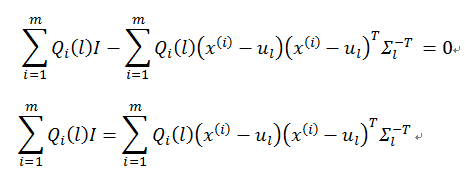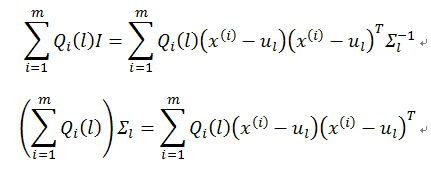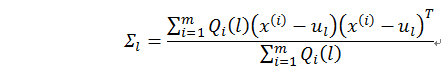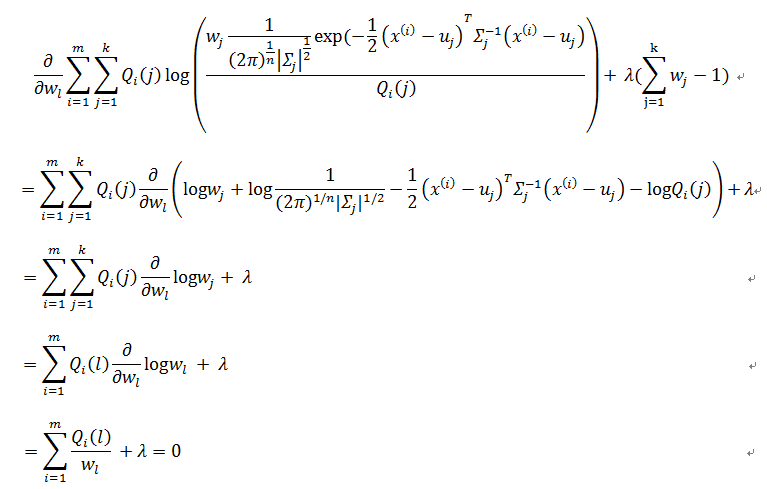EM算法与GMM的训练应用

注：本文主要参考Andrew Ng的Lecture notes 8，并结合自己的理解和扩展完成。本文有的数学推导过程并不是那么的严密，主要原因是本文的目的在于理解原理，若数学推导过于严密则文章会过于冗长。

GMM简介

GMM(Gaussian mixture model) 混合高斯模型在机器学习、计算机视觉等领域有着广泛的应用。其典型的应用有概率密度估计、背景建模、聚类等。

图1 GMM用于聚类

图2 GMM用于概率密度估计

图3 GMM用于背景建模

我们以聚类为例子进行简单讨论。如图1所示，假设我们有m个样本点，其坐标数据为{ x(1) , x(2) , x(3) ,…, x(m) }(注： x(i) 为向量)。假设m个数据分别属于k个类别(图1中k=2)，且不知道每个样本点 x(i) 属于哪一个类。假设每个类的分布函数都是高斯分布，那我们该如何求得每个点所属的类别?以及每个高斯分量的参数？我们先尝试最大似然估计。

回顾最大似然估计(MLE)的思想：已经出现的样本，应该是出现概率最大的样本。有似然函数：

L(θ)=∏i=1mp(x(i),z(i);u,Σ,ϕ)

L(θ) 就是当前m个样本出现个概率，我们使其最大化就得到了 θ 的估计值 θ^ ; p(x(i),z(i);u,Σ,ϕ) 是样本 x(i) 出现的概率； z(i) 是指第i属于z类；u是高斯分布的均值； Σ 是高斯分布的方差； ϕ 为其他参数。为计算方便，对上式两边取对数，得到对数似然函数。

l(θ)=log(L(θ))=log(∏i=1mp(x(i),z(i);u,Σ,ϕ))=∑i=1mlog(p(x(i),z(i);u,Σ,ϕ))

上说道，GMM的表达式为k个高斯分布的叠加，所以有

p(x(i),z(i);u,Σ,ϕ)=∑z(i)=1mp(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ)

p(z(i);ϕ) 为 p(z(i)) 为 z(i) 的先验概率。上式中x和z为自变量； u,Σ,ϕ 为需要估计的参数。 p(x(i)|z(i);uz(i),Σz(i)) 为高斯分布我们可以写出解析式，但是 p(z(i);ϕ) 的形式是未知的。所以不能直接对 l(θ) 求偏导取极值。考虑到 z(i) 不能直接由观测得到，称其为隐藏变量(latent variable)。此时的参数估计问题可以写为下式

argmaxl(θ)=argmax∑i=1mlog(∑z(i)=1mp(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ))

为了求解上式，引入EM算法(Expectation-Maximization Algorithm)。我们从Jensen不等式开始讨论EM算法。

Jensen不等式

若实函数f(x)存在二阶导 f′′(x) 且有 f′′(x)≥0 ，则f(x)为凸函数(convex function 注：此处的定义可能与国内教材不同)。 f(x) 的值域为 I ，则对于

a,b∈I,0≤λ≤1

有以下不等式成立：

f(λa+(1−λ)b)≤λf(a)+(1−λ)f(b)

其实也就是讲，区间 (a,b) 上任意一点 y 的函数值 f(y) 都位于其割线下方。几何解释如下

图4 凸函数的几何解释

需要说明的是，若f(x)为凹函数则不等式的方向取反。对上式进行推广，便可得到Jensen不等式(Jensen’s Inequality)。倘若有 f(x) 为凸函数，且

λ1,λ2,λ3…λk∈[0,1]

Σki=1λi=1

则有

f(λ1x1+λ2x2…λkxk)≤λ1f(x1)+λ2f(x2)+...λkf(xk)

此结果可由数学归纳法得到，在这里不做详细的描述。值得注意的是，如果Jensen不等式中的 k→∞ ，而且把 λi 看做概率密度，则有

f(∑ki=1λixi)≤∑ki=1λif(xi)

f(E(x))≤E(f(x))

上式成立的依据是， k→∞ ， λi 为概率密度时，

f(E(x))=∑ki=1λixi

且

E(f(x))=∑ki=1λif(xi)

在后续的EM算法推导中，会连续多次应用到Jensen不等式的性质。

EM算法

现在重新考虑之前的对数似然函数

l(θ)=log(L(θ))=log(∏i=1mp(x(i),z(i);u,Σ,ϕ))=∑i=1mlog(∑z(i)=1mp(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ))

直接对上式进行最大化求解会比较困难，所以我们考虑进行一定的变通。假设 Qi(z) 是某种概率密度函数,有 Qi(z)≥0 且 ∑Qi(z)=1 。现在对 l(θ) 的表达式进行一定得处理，先乘以一个 Qi(z) 再除以一个 Qi(z) ，有

l(θ)=∑i=1mlog(∑z(i)=1kp(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ))=∑i=1mlog(∑z(i)=1kQi(Z(i))Qi(Z(i))p(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ))=∑i=1mlog(∑z(i)=1kQi(Z(i))p(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ)Qi(Z(i)))

我们把 p(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ)Qi(Z(i)) 看做是 Z(i) 的函数；把 Qi(Z(i)) 看做是某种概率密度，则有

∑z(i)=1kQi(Z(i))p(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ)Qi(Z(i))=E(p(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ))

考虑到log函数为凹函数，利用Jensen不等式有

l(θ)=∑i=1mlog(∑z(i)=1kQi(Z(i))p(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ)Qi(Z(i)))≥∑i=1m∑z(i)=1kQi(Z(i))log(p(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ)Qi(Z(i)))

此时我们找到了 l(θ) 的一个下界。而且这个下界的选取随着 Qi(z) 的不同而不同。即我们得到了一组下界。用下图来简单描述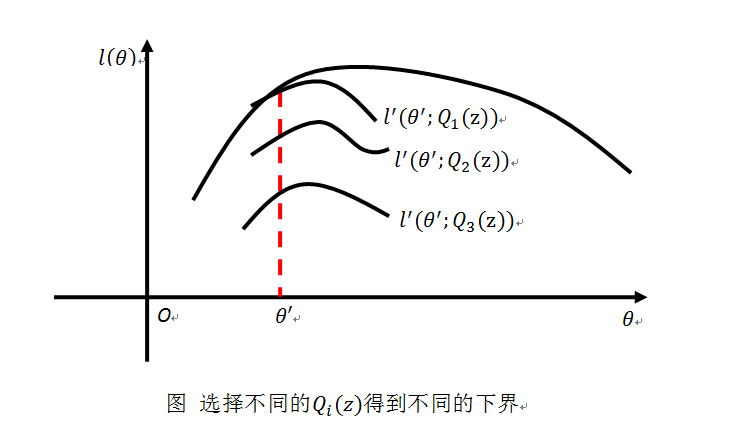

我们的目的是最大化 l(θ) ，如果我们不断的取 l(θ) 的最优下界，再优化最优下界，等到算法收敛就得到了局部最大值。先考虑 l(θ) 的最优下界。上式在等号成立时 l(θ) 取得最优下界。根据Jensen不等式的性质，取得等号时的条件有

p(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ)Qi(Z(i))=c

c 是不依赖于 z(i) 的常数。此时如果选取 Qi(z(i))∝P(x(i),z(i);θ) 就可使得上式成立。又考虑到 ∑z(i)Qi(z(i))=1 ，所以我们可以取

Qi(zi(i))=p(x(i),z(i);uz(i),Σz(i))Σkz(i)=1p(x(i),z(i);uz(i),Σz(i))=p(x(i),z(i);uz(i),Σz(i))p(x(i),z(i),Σz(i))=P(z(i)|x(i);z(i),Σz(i))

所以 Qi(zi) 取后验概率的时候 l′(θ) 是 l(θ) 最优下界。如果此时在下界 l′(θ) 的基础上优化参数 θ 使其最大化，则可进一步抬高 l(θ) 。如此循环往复的进行：取最优化下界；优化下界，便是EM算法的做法。接下来正式给出EM算法的步骤：

算法开始

E-step:取似然函数的最优下界，对于每个训练样本 x(i) 计算 Qi(z(i))=P(z(i)|x(i);θ) 。

M-step:优化下界，即求取

argmax∑mi=1∑kz(i)=1Qi(Z(i))log(p(x(i)|z(i);uz(i),Σz(i))p(z(i);ϕ)Qi(Z(i))) 。

判断 l(θt+1)−l(θt)<ε 是否成立，若成立则算法结束。 ε 是设定的算法收敛时 l(θ) 的增量。

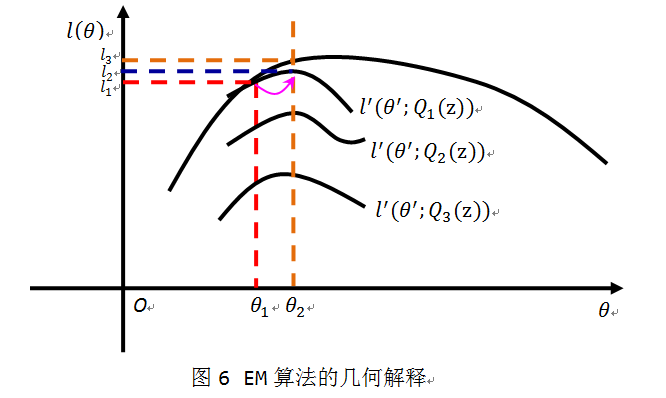
这就是一个不断取最优下界，抬高下界的过程。用下图简单的表示一个迭代过程:

我们可以这样解释：E-step就是取 l(θ) 的最优下界，此处是 l′(θ′;Q1(z)) 。在M-step，我们优化下界，通过调整 θ 使得 l′(θ′;Q1(z)) 取得局部最优值。由于Jensen不等式始终成立， l(θ) 始终大于等于下界 l′(θ′;Q1(z)) ，所以 l(θ) 的值从 l1 变为 l3 实现上升。那么这样的迭代是否是收敛的呢？

假设在t时刻的参数为θ^t此时的似然函数值为 l(θt) 。接下来进行EM算法迭代，在E-step

第二步利用了Jensen不等式。在M-step有

所以有

上式第二步中再次用到Jensen不等式。所以似然函数 l(θ) 会一直单调递增，直到到达局部最优值。利用图6来解释的话我们可以这样看：在E-step我们选取了最优下界 l′(θ′;Q1(z)) ,此时 l(θt)=l1 ；在M-step我们优化 l′(θ′;Q1(z)) 得到 l2 ；最后Jensen不等式一直都成立，所以有 l(θt+1)=l3≥l2≥l1 ，即 l(θt+1)≥l(θt) ，收敛性得到保障。

GMM的训练

对于GMM，其表达式为

wj 是每个gauss分量的权重。在E-step有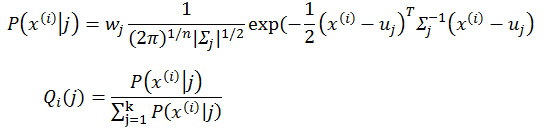

对于M-step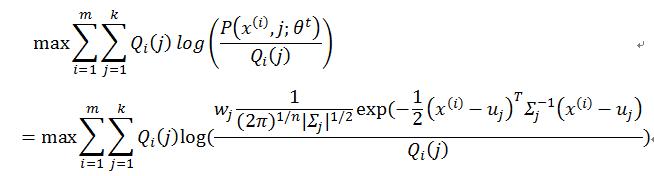

其中需要优化的参数为均值 u ，协方差矩阵 Σ ，权重 w 。分别对其求偏导:

令

解出

ul=Σmi=1Qi(l)x(i)Σmi=1Qi(l)

这便是第l个高斯分量均值 ul 在M-step的更新公式。

对于协方差矩阵Σ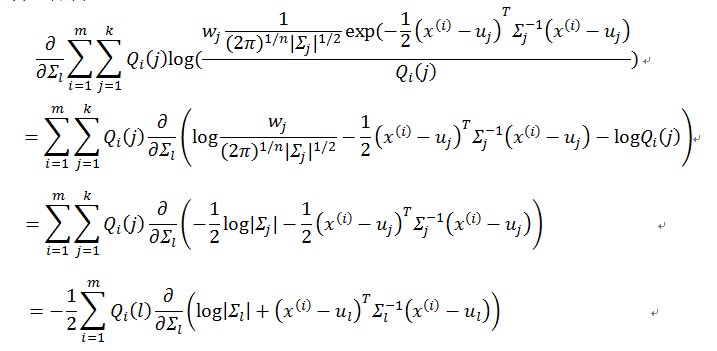

考虑到

所以有

等价于

Σl 为对称阵， Σ−Tl=Σ−1l ，所以有

解出协方差矩阵Σ_l的更新公式为

以上便是协方差矩阵 Σl 的更新公式

对于每个gauss分量的权重w_l(或者说是先验概率)，考虑到有等式约束

∑kj=1wj=1

应用Lagrange乘子法

所以有

wl=∑mi=1Qi(l)−λ

考虑到

Σkj=1wj=1

联立方程可得

λwl=−m=1mΣmi=1Qi(l)

这便是 wl 的更新公式。

以上完成了GMM训练的所有公式推导。

Matlab实现

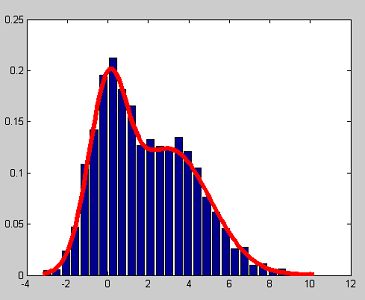
根据以上推导，可以很容易实现EM算法估计GMM参数。现以1维数据2个高斯混合概率密度估计作为实例，详细代码如下所示。

% fitting_a_gmm.m
% EM算法简单实现
% Hongliang He 2014/03 
clear
close all
clc

% generate data
len1 = 1000;
len2 = fix(len1 * 1.5);
data = [normrnd(0, 1, [1 len1])  normrnd(4, 2, [1 len2])] + 0.1*rand([1 len1+len2]);
data_len = length(data);

% use EM algroithm to estimate the parameters
ite_cnt = 100000;     % maximum iterations
max_err = 1e-5;  % 迭代停止条件

% soft boundary EM algorithm
z0 = 0.5;   % prior probability
z1 = 1 - z0;
u  = mean(data);
u0 = 1.2 * u;
u1 = 0.8 * u;
sigma0 = 1;
sigma1 = 1;

itetation = 0;
while( itetation < ite_cnt )
    % init papameters
    w0 = zeros(1, data_len);  % Qi, postprior 
    w1 = zeros(1, data_len);

    % E-step, update Qi/w to get a tight lower bound
    for k1=1:data_len
        p0 =  z0 * gauss(data(k1), u0, sigma0);
        p1 =  z1 * gauss(data(k1), u1, sigma1);
        p = p0 / (p0 + p1);

        if p0 == 0 && p1 == 0
            %p = w0(k1);
            dist0 = (data(k1)-u0).^2;
            dist1 = (data(k1)-u1).^2;
            if dist0 > dist1
                p = w0(k1) + 0.01;
            elseif dist0 == dist1
            else
                p = w0(k1) - 0.01;
            end
        end
        if p > 1
            p = 1;
        elseif p < 0
            p = 0;
        end


        w0(k1) = p;  % postprior 
        w1(k1) = 1 - w0(k1);
    end

    % record the pre-value
    old_u0 = u0;
    old_u1 = u1;
    old_sigma0 = sigma0;
    old_sigma1 = sigma1;

    % M-step, maximize the lower bound
    u0 = sum(w0 .* data) / sum(w0);
    u1 = sum(w1 .* data) / sum(w1);
    sigma0 = sqrt( sum(w0 .* (data - u0).^2) / sum(w0));
    sigma1 = sqrt( sum(w1 .* (data - u1).^2) / sum(w1));
    z0 = sum(w0) / data_len;
    z1 = sum(w1) / data_len;

    % is convergance
    if mod(itetation, 10) == 0
        sprintf('%d: u0=%f,d0=%f u1=%f,d1=%f\n',itetation, …
u0,sigma0,u1,sigma1)
    end

    d_u0 = abs(u0 - old_u0);
    d_u1 = abs(u1 - old_u1);
    d_sigma0 = abs(sigma0 - old_sigma0);
d_sigma1 = abs(sigma1 - old_sigma1);

% 迭代停止判断
if d_u0 < max_err && d_u1 < max_err && …
d_sigma0 < max_err && d_sigma1 < max_err
        clc
        sprintf('ite = %d, final value is', itetation)
        sprintf('u0=%f,d0=%f  u1=%f,d1=%f\n', u0,sigma0,u1,sigma1)
        break;
    end

    itetation = itetation + 1;
end

% compare
my_hist(data, 20);
hold on;
mi = min(data);
mx = max(data);
t  = linspace(mi, mx, 100);
y  = z0*gauss(t, u0, sigma0) + z1*gauss(t, u1, sigma1);
plot(t, y, 'r', 'linewidth', 5);

% gauss.m
% 1维高斯函数
% Hongliang He 2014/03
function y = gauss(x, u, sigma)
    y = exp( -0.5*(x-u).^2/sigma.^2 ) ./ (sqrt(2*pi)*sigma);
end

% my_hist.m
% 用直方图估计概率密度
% 2013/03
function my_hist(data, cnt)
    dat_len = length(data);
    if dat_len < cnt*5
        error('There are not enough data!\n')
    end

    mi = min(data);
    ma = max(data);
    if ma <= mi
        error('sorry, there is only one type of data\n')
    end

    dt = (ma - mi) / cnt;
    t  = linspace(mi, ma, cnt);
    for k1=1:cnt-1
        y(k1) = sum( data >= t(k1) & data < t(k1+1) );
    end
    y = y ./ dat_len / dt;
    t = t + 0.5*dt;
    bar(t(1:cnt-1), y);
    %stem(t(1:cnt-1), y)
end

最终运行结果

---

参考文献：

1. cs229-notes8

2. The Matrix Cookbook

3. Inequalities for Convex Functions (Part I) by Dragos Hrimiuc