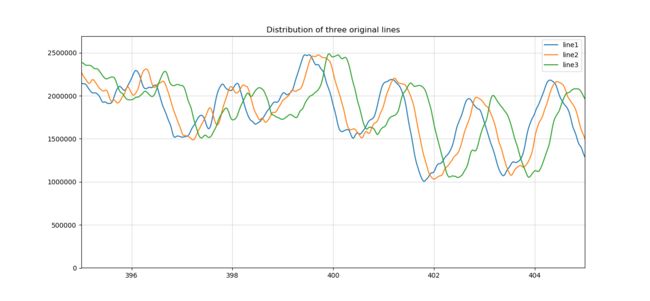
基于曲线最大值处理相位偏差

算法原理：

1.        求出第一条曲线的最大值对应的横坐标X1

2.        在X1附近检索第二条曲线的最大值所对应的横坐标X2

3.        求取gap=X2-X1

4.        以step=0.001，通过while迭代，更新gap+=i*step，使得sumErr=sum(abs(第一条曲线-第二条曲线))最小，得最终gap。（通过线性插值方法，只考虑t为50至550数据段，计算sumErr）

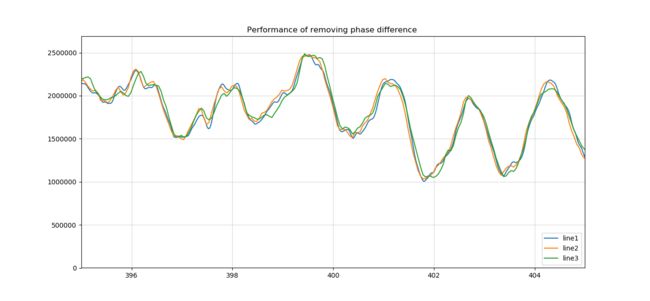
5.        同理，平移第三条曲线

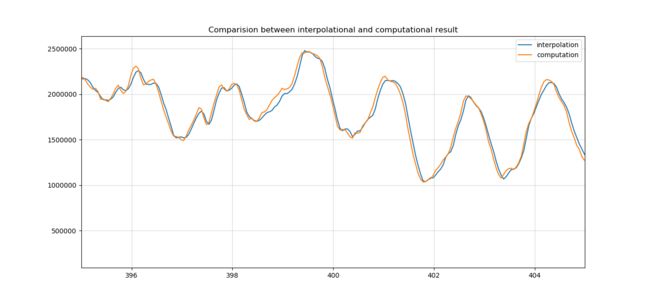
6.        计算第一条与第三条的线性插值结果，并计算插值结果与第二条曲线的误差

                                                                                    处理前

                                                                                    处理后

                                                                          插值结果与计算结果对比

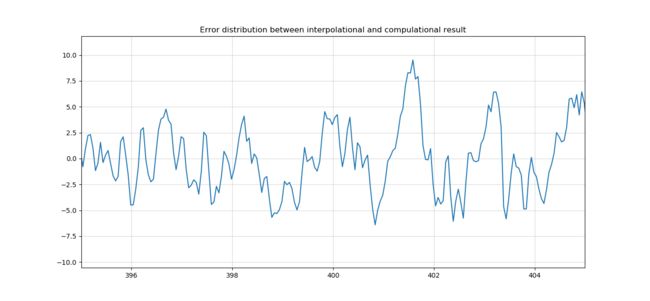
                                                                            插值结果与计算结果相对误差（%）分布

import numpy as np
from scipy import interpolate
import pylab as pl
from numpy import *


#导入数据
def loadData(name):
	fr=open(name)
	title=name.split('\\')[-1].split('.')[0]
	print(title)
	arrayOLines=fr.readlines()
	numOfLines=len(arrayOLines)
	index=0
	data=zeros((numOfLines-3,4))
	for line in arrayOLines[3:numOfLines]:
		line=line.strip()
		listFromLine=line.split('\t')
		data[index,:]=listFromLine[0:4]
		index+=1
	return data,title


###查找最大值的横坐标标号	
def findMaxNumber(data):
	linenub=0
	maxnub=0
	length=len(data)
	for i in range(3,length):
		if abs(data[i])>abs(maxnub):
			linenub=i
			maxnub=data[i]
	return linenub,maxnub

#查找最佳平移距离	
def findGap(data,xnew,linenub1,j):
	dis=10
	linenub,maxnub=findMaxNumber(data[linenub1-dis:linenub1+dis,j])
	print('----------%d号线最大值（%s）对应的时间是 %f------------'%(j,maxnub,data[linenub1-dis+linenub,0]))
	gap=data[linenub1-dis+linenub+1,0]-data[linenub1,0]
	print ('------------初始间隔是 %s------------'%gap)

	adjust=True
	sumerr=111111111111111111111110
	i=0
	step=0.001
	f1=interpolate.interp1d(data[:,0],data[:,1],kind="slinear")
	ynew1=f1(xnew)
	while(adjust):
		print('--------------第%d次修正---------'%i)
		gap+=step
		f3=interpolate.interp1d(data[:,0]-gap,data[:,j],kind="slinear")
		i+=1
		ynew3=f3(xnew)
		err=abs(ynew3-ynew1)
		sumerrtemp=sum(err)/len(err)
		if(sumerrtemp>sumerr):
			adjust=False
		else:
			sumerr=sumerrtemp
	gap=gap-step
	print('-----------最终平移间隔是 %f--------------'%gap)
	return gap
	
	
def main():
	
	xnew=np.linspace(50,550,10000)
	name=r'E:\model\Post\Rotating hub Myz.txt'
	data,title=loadData(name)
	linenub1,maxnub1=findMaxNumber(data[:,1])
	time=data[linenub1,0]
	print('----------1号线最大值（%s）对应的时间是 %f------------'%(maxnub1,time))
	gap2=findGap(data,xnew,linenub1,2)
	gap3=findGap(data,xnew,linenub1,3)
	minx=395
	maxx=405
	
	pl.figure()
	ax1=pl.subplot(111)
	ax1.grid(True,alpha=0.5)
	pl.plot(data[:,0],data[:,1])
	pl.plot(data[:,0],data[:,2])
	pl.plot(data[:,0],data[:,3])
	pl.xlim(minx,maxx)
	pl.legend(["line1","line2","line3"])
	pl.title("Distribution of three original lines")
	
	#显示平移后的三条曲线
	pl.figure()
	ax2=pl.subplot(111)
	ax2.grid(True,alpha=0.5)
	f1=interpolate.interp1d(data[:,0],data[:,1],kind="slinear")
	ynew1=f1(xnew)
	pl.plot(data[:,0],data[:,1])
	
	f2=interpolate.interp1d(data[:,0]-gap2,data[:,2],kind="slinear")
	ynew2=f2(xnew)
	pl.plot(xnew,ynew2,label=str("slinear"))
	
	f3=interpolate.interp1d(data[:,0]-gap3,data[:,3],kind="slinear")
	ynew3=f3(xnew)
	pl.plot(xnew,ynew3,label=str("slinear"))
	pl.xlim(minx,maxx)
	pl.legend(["line1","line2","line3"],loc="lower right")
	pl.title("Performance of removing phase difference ")
	
	#对比插值结果与计算结果
	interpolation=(ynew1+ynew3)/2
	pl.figure()
	ax3=pl.subplot(111)
	ax3.grid(True,alpha=0.5)
	pl.plot(xnew,interpolation)
	pl.plot(xnew,ynew2)
	pl.xlim(minx,maxx)
	pl.legend(["interpolation","computation"])
	pl.title("Comparision between interpolational and computational result")
	
	#显示插值结果与计算结果的误差分布
	err=(interpolation-ynew2)/ynew2*100
	pl.figure()
	ax4=pl.subplot(111)
	ax4.grid(True,alpha=0.5)
	pl.plot(xnew,err)
	pl.title("Error distribution between interpolational and compulational result")
	pl.xlim(minx,maxx)
	pl.show()
		
	
if __name__=='__main__':
	main()