红黑树
引入:
结合上一篇普通的二叉树作为数据工具有着重要的优势:可以快速地找到一个给定关键字的数据项,并且可以快速地插入和删除数据项。但是,二叉树同时也存在一个很麻烦的问题,如果二叉树中插入的是随机数据,则执行小姑很好,但是如果插入的是有序数据(1,2,3,4,5)或者是逆序数据(5,4,3,2,1),速度就和变得特别的慢。因为当插入的数据为有序的话,那么二叉树就是非平衡的了。而对于非平衡的二叉树,它的快速查找(插入、删除)指定数据项的能力就丧失了。
红-黑树:
他就是增加了某些特点的二叉搜索树。
平衡树和非平衡树:
在之前学习过的二叉树的例子中,假如插入一系列关键字有序的数据项,其关键之是升序或者降序的,都会得到一个不平衡的树。在上述的不平衡树中,所有的节点走排列在一条直线上,没有分支。当树没有了分支,它其实就是一个链表,数据的排列是一维的而不是二维的。原树结构的查找速度O(logN)就变成了现在的O(N),效率下降非常明显,同样是10000个数据项的非平衡树中搜索数据项平均需要5000次比较左右,而在随机插入生成的平衡树中搜索数据项只需要14次比较。所以对于已经知道有序的数据项首先使用链表也无妨。
如何补救非平衡树?
为了保持较快的时间O(logN)去访问一棵树,需要保证树的结构是平衡的。这就是说一棵树在它左边的后台数目和在它右边的后代数目应该大致相同。这就引出了 红-黑树,红黑树的有序是在插入的时候取得的(删除也是,但是暂时忽略这个问题),对于一个要插入的数据,要例行检查不会破坏树一定的特性。如果破坏了,程序就会进行纠正,根据需要更改树的结构,通过维持树的特性,保持了树的平衡。
红-黑树的特性:
首先是红黑树的两个特点,一个简单一个复杂:
1. 节点又有颜色
2. 在插入和删除的过程中,要遵循保持这些颜色的不同排列的规则。
然后是红–黑规则:****非常重要
1. 每一个节点不是红色的就是黑色的
2. 根总是黑色的
3. 如果节点是红色的,则它的字节点必须是黑色的(反之倒不一定要符合)
4. 从根到叶节点或者空子节点的每一条路径,都必须包含相同数目的黑色节点。
附:从根到叶节点的路径上的黑色节点数目,称为黑色高度。所以规则4也可以说是:所有根到子叶的路径上黑色高度必须相同。
红–黑规则和平衡树:
创建一棵树,他虽然已经超过两层不平衡了,但却要满足红黑规则。实时证明这是不可能的。这就是为什么红黑规则可以保持树是平衡的。如果一条路径上的节点数比另一条路径上的节点数多一个以上,那它要么有更多的黑色节点,违背了规则4要么有两个相邻接的红色节点,违背了规则3。
红黑树保持平衡的两个手段之旋转:
为了平衡一棵树,需要重新手动地排列节点。例如,如果所有的节点都在根的左侧,就需要把一些节点移到右侧。这是用旋转来实现。旋转必须一次做的两件事:
1. 使一些节点上升,一些节点下降,帮助树平衡
2. 保证不破坏二叉搜索树的特征
红黑树保持平衡的两个手段之颜色变换:
为了使一棵树保持平衡,就得使其满足红黑规则,然而一棵树不可能自然而然的满足红黑规则,所以需要代码去做一些事情,首先是,颜色变换。
什么是旋转?
旋转改变的只是节点之间的关系,选择一个节点作为旋转的顶端(top),如果做一次右旋,这个顶端节点将会向下或者向右移动到它右子节点的位置。它的左子节点将会上移到它原来的位置。顶端节点不是旋转的中心。
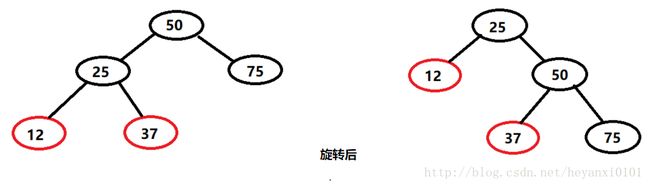
对于左图而言,节点37称为顶端节点50的内子孙节点。(节点12称为是节点50的外子孙节点)对于内子孙节点而言,如果它是上移节点(在右旋转过程中是顶端节点的左子节点)的子节点,它总是要断开和父亲节点的连接并且重新连接到它以前的祖父节点上。这就好像是称为自己的叔叔一样。(注意图中节点37的位置变化)。上面说到的就是奇怪的横向移动节点问题。
接下来是移动子树问题,先上图
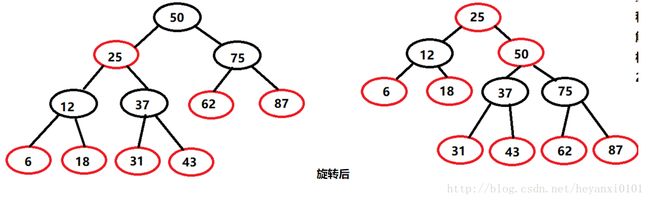
OK,我们可以看出在进行旋转之后,发生了以下事情:
1. 顶端节点(50)移动到它右子节点的位置
2. 顶端节点的左子节点(25)移动到了顶端的位置上
3. 以节点(12)为根的整棵子树都向上移动了
4. 以节点(37)为根的整棵子树横向移动了,成为节点(50)的左子节点
5. 以节点(75)为根的整棵子树都向下移动了
在上面的红黑树的旋转过程中,我们发现整棵子树都会移动的现象。
在红黑树中插入一个新节点:
在下面的叙述中,使用X、P、G表示关联的节点。X表示违反规则的节点。(有时候X指新插入的节点,有时候在父节点和子节点发生红–红颜色冲突时指子节点)
X–> 一个特殊的节点
P–> P是X的父节点
G–> G是X的祖父节点(P的父节点)
· 在顺着树向下查找插入点的时候,只要发现一个黑色节点有两个红色的子节点(违反规则2)就执行一次颜色变换。
为什么?因为,当一个黑色的节点有两个红色的节点的时候,要插入一个节点的话,肯定要插在那两个红色的子节点的子节点位置上,但是加入插入的节点是红色的话就违反了规则2,加入是黑色的话又肯定违反了规则4,所以就要执行一次颜色变换。
· 有时颜色变换会造成红–红颜色冲突(违反规则3),称红色子节点为X,红色父节点为P。只用一次或者两次旋转就可以解决这个冲突,旋转的次数是由X是G的外侧子孙节点还是内侧子孙节点决定的。
为什么?因为,当发生旋转的时候,这些所谓的内侧子孙节点或者是外侧子孙节点就会断开和自己付节点的连接,并且重新连接到自己原来的祖父节点上。
· 在完成节点X的插入之后,如果P是黑色的,只需要连接这个新的红色节点,如果P是红色的,则有两种可能:X是G的外侧子孙节点,或者X是G的内侧子孙节点。需要两次改变节点颜色。如果X是外侧节点,则执行一次旋转,如果X是内侧节点,则执行两次旋转。这能使得树达到平衡状态。
接下来是三个问题的分析:
1. 在下行路途中的颜色变换
2. 插入节点之后的旋转
3. 在向下路途上的旋转
1. 在下行路途中的颜色变换
假设插入的过程顺着树的顶端向下执行,在每一个节点处向左或者向右走,查找插入新节点为位置。为了不违反颜色规则,有必要的时候需要进行颜色变换。
规则是:每当查找例程遇到一个有两个红色子节点的黑色节点时,它必须把子节点变为黑色,而把父节点变为红色(除非父节点为根,根总是黑色的)。
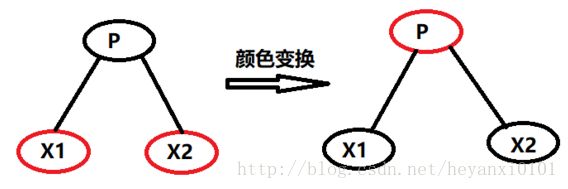
黑色高度不变:这次变换没有改变从根向下过P到叶节点或者空节点的路径上的黑色节点的数目,在变换之后,P不再是黑色的了。但是X1和X2都是黑色的,所以三角形仍然为通过它的每条路径贡献一个黑色节点。因此颜色变换不会造成违背规则4。
违背规则3:虽然这种变换不会违背规则4,但是可能会违背规则3(一个节点和其父节点不能同时为红色的),如果P的父节点是黑色的,那么不会有任何问题,但是假如P的父节点是红色的,那么在P的颜色变换之后,就会出现违反规则3的情况。
根的情况:根对其两个子节点进行颜色变换的时候,根和它的子节点一样都是黑色的。
2. 在插入节点之后的旋转
首先新插入的X节点总是红色的,X可能插到相对于P(X的父节点)和G(P的父节点)不同的位置上,下面是各种位置的情况。
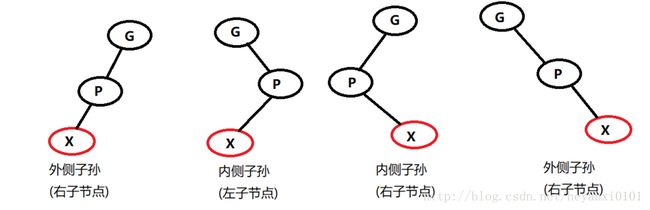
在要插入的X节点相对于原来不同文位置的情况下,有三种可能性需要我们考虑:
1. P是黑色的
2. P是红色的,X是G的一个外侧子孙节点
3. P是红色的,X是G的一个内侧子孙节点
解决不同的情况:
1. 如果P是黑色的,那么啥都不做,直接插入即可。
2. 如果P是红色的,且X是G的一个外侧子孙节点,则需要一次旋转和一些颜色的改变。
3. 如果P是红色的,且X是G的一个内侧子孙节点,则需要两次旋转和一些颜色的改变。
3. 在下行路途中的旋转
在向下的路径上可能会有两种旋转的可能性,分别对应前面描述的在插入阶段的可能性2和可能性3.违背规则的节点可能是一个外侧子孙节点,也有可能是一个内侧子孙节点。
1. 外侧子孙节点:必须要执行两次颜色改变和一次旋转。
2. 内侧子孙节点:需要两次旋转来改正。
红黑树的效率
和一般的二叉搜索树类似,红黑树的查找、插入、删除的时间复杂度为O(log2N)。实际上在红黑树中的查找大约需要log2N次比较,查找不可能需要超过2log2N次比较。
插入和删除的时间要增加一个时间因子,因为不得不在下行的路径上和插入点执行颜色变换和旋转,平均下来每插入一次数据大约需要一次一次旋转,所以插入 的时间复杂度还是log2N,但是比二叉搜索树包慢一点了。
但是在大多数的应用中,查找的次数比插入和删除的次数多,所以应用红黑树取代普通的二叉搜索树总体上来说不会增加太多的额外开销。
其他的平衡树:
AVL树是最早的平衡树。在AVL树中每一个节点存储一个额外的数据,它的左子树和右子树的高度差。这个差值不会大于1.也就是说,节点的左子树的高度和右子树的高度相差不会大于1层。
插入之后,检查新节点插入点所在的最低子树的根。如果它的子节点的高度相差大于1,执行一次或者两次旋转使它们的高度相等。然后算法向上移动,检查上面的节点,必要时均衡高度。
这个AVL树查找的时间复杂度为O(logN),因为树一定是平衡的。但是由于插入或者删除一个节点时需要扫描两趟树,一次向下查找节点,一次向上平衡树,AVL树不如红黑树高效,也不如红黑数常用。
红黑树其实就是智能版的二叉树,在原二叉树的基础上,增加了颜色还有自我调整的功能,该树可以自己调整自己的结构使其一直保持一种相对平衡的状态,利用自身的颜色变换还有旋转使其的结构一直处于相对平衡状态,然后增使其在任何数据面前的表现的十分优异。