层次主题模型——Hierarchical LDA
在LDA主题模型提出后,其在很多领域都取得了很成功的应用,如生物信息、信息检索和计算机视觉等。但是诸如LDA之类的主题模型,将文档主题视为一组“flat”概率分布,一个主题与另一个主题之间没有直接关系,因此它们能够用于挖掘语料中蕴含的主题,但是无法发现主题之间的关联和层次。对于每一篇文档,主题层次是显而易见的,是一个由粗到细,由宽泛到具体逐渐层层递进,逐渐细化。于是,LDA的作者Blei教授在LDA的基础上提出了hierarchical Latent Dirichlet Allocation(hLDA),下图给出了主题层次的示例:
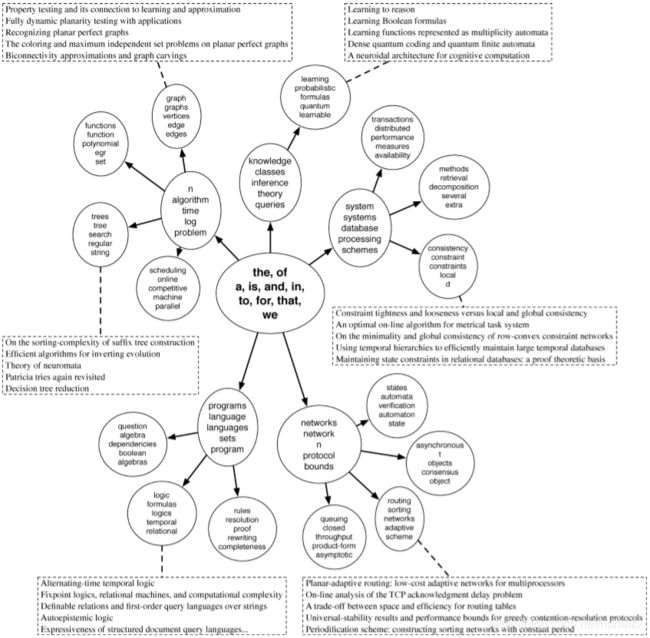
作者将主题的层次结构也看作是随机变量,通过中国餐馆过程(Chinese Restaurant Process,CRP)的变种嵌套中国参观过程(nested Chinese Restaurant Process,nCRP)作为主题层次结构的先验,然后由算法程序根据语料推导出最佳主题层次结构。因此,下面将从CRP开始,复盘hLDA的整个流程。
Chinese Restaurant Process(CRP)
中国餐馆过程是一个时间离散的(discrete-time)随机过程,在任意整数时间 n n n,该随机过程的值是集合 { 1 , 2 , … , n } \{1,2,\dots,n\} {1,2,…,n}的一个划分 B n B_n Bn。可以想象这么一个场景:
- 假设有一个有无数餐桌的中国餐馆,每张桌子可以坐无限人。
- 第一位顾客坐在第一张桌子上,对于其后的第 m m m位顾客,其坐在哪张桌子上由以下概率给出
(1) p ( o c c u p i e d t a b l e i ∣ p r e v i o u s c u s t o m e r s ) = m i γ + m − 1 p ( n e x t u n o c c u p i e d t a b l e ∣ p r e v i o u s c u s t o m e r s ) = γ γ + m − 1 \begin{aligned} p(occupied\space table\space i\space |\space previous\space customers)=\frac{m_i}{\gamma+m-1}\\ p(next\space unoccupied\space table\space |\space previous\space customers)=\frac{\gamma}{\gamma+m-1} \end{aligned}\tag 1 p(occupied table i ∣ previous customers)=γ+m−1mip(next unoccupied table ∣ previous customers)=γ+m−1γ(1)其中, m i m_i mi表示第 i i i张桌子此时已有的顾客数, m − 1 m-1 m−1表示这位顾客之前餐馆已有的顾客总数, γ \gamma γ是CRP的超参数,用于控制分出的桌子数目, γ \gamma γ越大,最后分出的桌子可能越多。该过程不受用户顺序以及桌子排列顺序影响,具有概率可交换性(exchangeabililty),同时CRP也反应了“富者愈富”的现象。
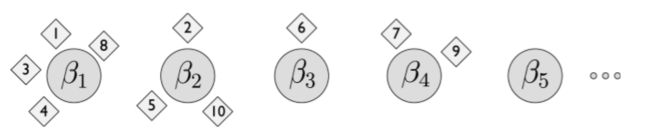
上图展示了10位顾客经过CRP的一种划分。与主题模型联系起来,每一张桌子可以看作是一个主题, β \beta β对应主题-单词分布,每一位顾客可以看作文档index,为该位置分配主题后,根据对应的主题-单词分布 β \beta β就能生成该位置的单词。
CRP可以很好的用于描述混合模型中成分数目的不确定(主题数目的不确定),但是其依旧无法刻画混合模型中各个成分之间的层次关系,于是作者对CRP进行了扩展,提出了nested Chinese Restaurant Process(nCRP)。
nested Chinese Restaurant Process(nCRP)
对于nCRP的定义可以想象如下场景:假设某城市中有无限数量的餐馆,每个餐馆有无限数量的桌子,每张桌子可以坐无限人。其中一个餐馆被指定为根餐馆,同时每个餐馆的每张桌子上都放有一张指向其他餐馆的卡片(每个餐馆只会被指向一次),因此城市中的餐馆可以构成一棵无限深度无限分支的树,每一个餐馆都与树中的某一层关联。根餐馆位于第一层,根餐馆中桌子上卡片指定的餐馆位于第二层……
当一位游客来到这座城市,第一天他进入了root餐馆并按照公式(1)选择 了一张桌子,第二天他按照第一天所坐桌上卡片的指示进入第二家餐馆,同样按照公式(1)选择一张桌子,经过 L L L天, 他光顾的餐馆构成了一条从根餐馆到 L L L层餐馆的路径,同样地, M M M位游客经过 L L L天旅游会形成 M M M条路径,M条路径的集合构成了无限深度无限分支树的子树。如下图展示了其中一颗子树。
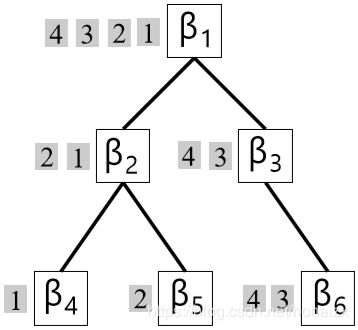
因此,我们能够采用nCRP表示主题层次结构的先验,因为,standard CRP能够表达主题数目的不确定性,nested CRP能够表达主题层次结构的不确定性。
hLDA
假定对于一棵给定的 L L L层树,树中每一个节点与一个主题关联,此时文档的生成过程如下:
- 选择一条从根节点到叶子节点的路径,确定文档主题;
- 从 L L L维Dirichlet先验分布 D i r ( α ) Dir(\alpha) Dir(α)中生成文档主题比例;
- 从根节点到叶子节点的主题混合中生成单词,主题混合比例为,单词生成概率为 p ( w ∣ θ ) = ∑ i = 1 L θ i p ( w ∣ z = i , β i ) p(w|\theta)=\sum_{i=1}^L\theta_ip(w|z=i,\beta_i) p(w∣θ)=∑i=1Lθip(w∣z=i,βi)。
上面描述的是主题层次结构给定的情况,因为nCRP给我们提供了一种定义主题拓扑先验的方法,我们因此可以借助nCRP放松固定树拓扑的假设。此时语料的生成过程如下:
(1) 对于无限树中每一个餐馆 k ∈ T k\in T k∈T:
\quad a) 生成一个主题 β k ∼ D i r ( η ) \beta_k\thicksim Dir(\eta) βk∼Dir(η)。
(2) 对每一篇文档 d ∈ { 1 , 2 , … , D } d\in \{1,2,\dots,D\} d∈{1,2,…,D}:
\quad a) 生成一条深度为 L L L的主题路径 :
\quad\quad (i) 指定 c 1 c_1 c1为根餐馆 ;
\quad\quad (ii) 对于每一层 l ∈ { 2 , … , L } l\in\{2,\dots,L\} l∈{2,…,L} ,采用公式(1)选择餐馆 c l − 1 c_{l-1} cl−1中一张桌子,将该桌子指定的餐馆设置为 c l c_l cl。
\quad b) 选择一个 L L L维文档-主题分布 θ d ∣ α ∼ D i r ( α ) \theta_d|\alpha\thicksim Dir(\alpha) θd∣α∼Dir(α)。
\quad c) 对于每一个单词 n ∈ { 1 , … , n } n\in\{1,\dots,n\} n∈{1,…,n}:
\quad\quad (i) 选择一个主题 z d , n ∣ θ d ∼ M u l t i ( θ d ) z_{d,n}|\theta_{d}\thicksim Multi(\theta_d) zd,n∣θd∼Multi(θd);
\quad\quad (ii) 生成单词 w n ∣ z d , n , c d , β ∼ M u l t i ( β c d [ z d , n ] ) w_n|{z_{d,n},c_d,\beta}\thicksim Multi(\beta_{c_d[z_{d,n}]}) wn∣zd,n,cd,β∼Multi(βcd[zd,n])。
其图模型如下图所示:

不同于层次聚类(hierarchical clustering)将每一个数据点(单词)设置为叶子节点,然后逐层向上合并相似的节点直至根节点,hLDA的中间节点不是孩子节点的进一步抽象,而是反应了共享该节点的文档路径的共同术语。从根节点向下深入的过程中,第一层是对文档的一个粗糙划分,其后每一层都是对该分区的文档的更细致划分,对应的主题也会更加具体。当生成 n n n个词时,最多有 n n n个节点被访问过,也即最多有 n n n个主题被生成,此时第 ( n + 1 ) (n+1) (n+1)个词既可以从之前的主题中生成,也可以来自一个新的主题。同样地,第 ( n + 1 ) (n+1) (n+1)篇文档既可以选择前面文档的路径,也可以在树中任意节点分裂出新的主题。
后验推断
CRP的概率可交换性保证了我们可以采用MCMC的方法进行后验推断,论文中作者采用了Gibbs sampling方法,采样算法涉及的变量包括: w d , n w_{d,n} wd,n表示第 d d d篇文档第 n n n个单词,其实唯一的可观测变量; c d c_{d} cd表示第 m m m篇文档的主题对应的餐馆; z d , n z_{d,n} zd,n表示第 m m m篇文档第 n n n个单词的主题分配,Gibbs Sampling就是在对 z d , n z_{d,n} zd,n和 c d c_{d} cd进行评估。
p ( c d , z d , n ∣ w , z − ( d , n ) , c − d , α , η , γ ) = p ( z d , n ∣ z − ( d , n ) , c , w , α , η ) ∗ p ( c d ∣ w , c − d , z , γ , η ) p(c_d,z_{d,n}|w,z_{-(d,n)},c_{-d},\alpha,\eta,\gamma)=p(z_{d,n}|z_{-(d,n)},c,w,\alpha,\eta)*p(c_d|w,c_{-d},z,\gamma,\eta) p(cd,zd,n∣w,z−(d,n),c−d,α,η,γ)=p(zd,n∣z−(d,n),c,w,α,η)∗p(cd∣w,c−d,z,γ,η)
因而Gibbs采样的过程可以分成两步:路径采样和主题层次分配采样。
Level allocation sampling
给定当前的路径分配,我们需要对第 d d d篇文档的第 n n n个单词分配主题层次 z d , n z_{d,n} zd,n。
(2) p ( z d , n ∣ z − ( d , n ) , c , w , α , η ) = p ( z d , n ∣ z − ( d , n ) , α ) ∗ p ( w d , n ∣ z , c , w − ( d , n ) , η ) p(z_{d,n}|z_{-(d,n)},c,w,\alpha,\eta)=p(z_{d,n}|z_{-(d,n)},\alpha)*p(w_{d,n}|z,c,w_{-(d,n)},\eta)\tag 2 p(zd,n∣z−(d,n),c,w,α,η)=p(zd,n∣z−(d,n),α)∗p(wd,n∣z,c,w−(d,n),η)(2)
Path sampling
给定主题层次分配,我们需要对每篇文档的路径进行采样,在给定其他所有路径和观察到的单词的情况下。
(3) p ( c d ∣ w , c − d , z , γ , η ) = p ( c d ∣ c − d , γ ) ∗ p ( w d ∣ c , w − d , z , η ) \begin{aligned} p(c_d|w,c_{-d},z,\gamma,\eta)=p(c_d|c_{-d},\gamma)*p(w_d|c,w_{-d},z,\eta) \end{aligned}\tag 3 p(cd∣w,c−d,z,γ,η)=p(cd∣c−d,γ)∗p(wd∣c,w−d,z,η)(3)
Gibbs Sampling算法
在给定采样器当前状态 { c 1 : D ( t ) , z 1 : D ( t ) } \{c_{1:D}^{(t)},z_{1:D}^{(t)}\} {c1:D(t),z1:D(t)}的情况下,基于条件概率迭代采样每一个变量
- 对每一篇文档 d ∈ { 1 , 2 , … , D } d\in \{1,2,\dots,D\} d∈{1,2,…,D}
- 根据公式 (3)随机生成 c d ( t + 1 ) c_d^{(t+1)} cd(t+1) ;
- 对文档中每一个单词,根据公式(2)随机生成 z d , n ( t + 1 ) z_{d,n}^{(t+1)} zd,n(t+1)。
总结
hLDA是一个非常优美的主题层次建模方法,当然其论文也非常的深奥难懂,可能本人的理解存在不正确的地方,欢迎大家交流讨论。
参考文献
Hierarchical Topic Models and the Nested Chinese Restaurant Process
The nested chinese restaurant process and bayesian nonparametric inference of topic hierarchies
Github hlda