【机器学习笔记】——Bagging、Boosting、Stacking（RF / Adaboost / Boosting Tree / GBM / GBDT / XGBoost / LightGBM）

目 录

集成学习

概念

  首先，让我们先来了解一下，什么是集成学习（Ensemble Learning，写作银桑，读作昂桑）。集成学习由训练数据构建一组基分类器，然后通过对每个基分类器的预测进行投票来进行分类，对每个个体学习器的预测进行（加权）平均来进行回归，有时也被称为多分类器系统、基于委员会的学习等。如果把单个分类器比作一个决策者的话，集成学习的方法就相当于多个决策者共同进行一项决策。严格来说，集成学习并不算是一种分类器，而是一种分类器结合的方法。

• 集成学习将多个分类方法聚集在一起，以提高分类的准确率。通常一个集成分类器的分类性能会好于单个分类器

  对于二分类问题，假设基分类器的错误率为$ϵ$：
$$P(h_i(x̸=y))=ϵ$$

  通过投票我们得到集成学习的分类预测：
$$H(x)=sign\left(\sum _{i=1}^T{h}_i(x)\right)$$

  假设分类器的错误率相互独立，则由Hoeffding不等式有：
$$P(H(x̸=y))=\sum _{k=0}^{\lfloor T/2\rfloor }\left(\genfrac{}{}{0ex}{}{T}{k}\right)(1-ϵ{)}^k{ϵ}^{T-k}\le exp\left(-\frac{1}{2}T(1-2ϵ{)}^2\right)$$

  即随着集成中基分类器数目$T$增大，集成的错误率会指数级下降，最终趋于0。当然实际中个体学习器错误率独立的假设是不成立的

• 集成学习的很多理论研究都是针对弱分类器（精度略高于50%）进行的，但在实践中往往会使用较强的分类器

• 个体学习器要有一定的“准确性”，并且要有“多样性”。一般的，准确性很高之后，要增加多样性就需牺牲准确性。如何产生并结合“好而不同”的个体学习器，恰是集成学习研究的核心

  下面这个例子，图(a)中每个学习器只有67%的精度，但集成学习却达到了100%；图(b)中三个学习器完全一样，集成之后性能没有提高；图©中每个学习器只有33%的精度集成学习的效果更差。

思维导图

Bagging算法

概念

  Bagging算法（Bootstrap AGGregatING）是一种并行式集成算法。它基于自助采样法（Bootstrap sampling）采样出T个含有m个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再将这些基学习器进行结合。

  算法的伪代码如下：

  从偏差-方差分解的角度看，降低一个估计的方差的方式是把多个估计平均起来，所以Bagging主要关注降低方差，因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显。同时，Bagging并不能减小模型的偏差，所以应尽量选择偏差较小的基分类器，如未剪枝的决策树。

编程（分类）

  参考：https://github.com/vsmolyakov/experiments_with_python/blob/master/chp01/ensemble_methods.ipynb

  我们用iris数据集来看一下不同基分类器Bagging的效果

import itertools
import numpy as np

import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec

from sklearn import datasets

from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier

from sklearn.ensemble import BaggingClassifier
from sklearn.model_selection import cross_val_score, train_test_split

from mlxtend.plotting import plot_learning_curves
from mlxtend.plotting import plot_decision_regions

np.random.seed(0)

  导入数据

iris = datasets.load_iris()
X, y = iris.data[:, 0:2], iris.target

X.shape, y.shape

((150, 2), (150,))

  设置基分类器和集成方法

# 配置基分类器的参数
clf1 = DecisionTreeClassifier(criterion='entropy', max_depth=1)    # 深度为1的决策树
clf2 = KNeighborsClassifier(n_neighbors=1)    # k=1的k近邻

# 每个Bagging有10个基分类器
bagging1 = BaggingClassifier(base_estimator=clf1, n_estimators=10, max_samples=0.8, max_features=0.8)
bagging2 = BaggingClassifier(base_estimator=clf2, n_estimators=10, max_samples=0.8, max_features=0.8)

  查看单个学习器和Bagging后的效果

label = ['Decision Tree(depth = 1)', 'K-NN(k = 1)', 'Bagging Tree', 'Bagging K-NN']
clf_list = [clf1, clf2, bagging1, bagging2]

fig = plt.figure(figsize=(10, 8))
gs = gridspec.GridSpec(2, 2)    # 创建 2x2 的画布
grid = itertools.product([0,1],repeat=2)    # 返回参数的笛卡尔积的元组，每个元素可以用 2 次

for clf, label, grd in zip(clf_list, label, grid):        
    scores = cross_val_score(clf, X, y, cv=3, scoring='accuracy')    # Array of scores of the estimator for each run of the cross validation.
    print("Accuracy: %.2f (+/- %.2f) [%s]" %(scores.mean(), scores.std(), label))
        
    clf.fit(X, y)
    ax = plt.subplot(gs[grd[0], grd[1]])
    fig = plot_decision_regions(X=X, y=y, clf=clf, legend=2)    # 绘制决策边界
    plt.title(label)

plt.show()

Accuracy: 0.63 (+/- 0.02) [Decision Tree(depth = 1)]
Accuracy: 0.70 (+/- 0.02) [K-NN(k = 1)]
Accuracy: 0.66 (+/- 0.02) [Bagging Tree]
Accuracy: 0.61 (+/- 0.02) [Bagging K-NN]

  可以发现决策树的集成有一定效果，而k近邻的效果反而变差了。这是因为k近邻是稳定学习器，不易受样本扰动影响。

  再来看看数据集的划分对训练结果的影响

#plot learning curves
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
    
plt.figure()
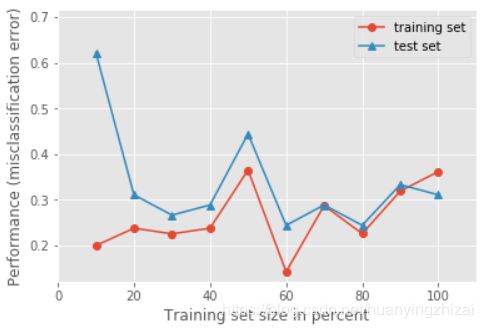
plot_learning_curves(X_train, y_train, X_test, y_test, bagging1, print_model=False, style='ggplot')
plt.show()

  虽然每次结果有较大的差异，但是我们还是能得到一些结论：对于给定的划分比例，模型在训练集上的错分率基本在30%上下，而在测试集上，当训练集较小时，模型在测试集上表现很差，当训练集比例逐渐增加时，模型在测试集上的表现慢慢变好，一般在训练集占到80%左右时，模型在训练集和测试集上都能取得较好的表现

  接下来我们看一下学习器的个数对bagging效果的影响

#Ensemble Size
num_est = np.concatenate(([1],np.arange(5,105,5)))
bg_clf_cv_mean = []
bg_clf_cv_std = []

for n_est in num_est:    
    bg_clf = BaggingClassifier(base_estimator=clf1, n_estimators=n_est, max_samples=0.8, max_features=0.8)
    scores = cross_val_score(bg_clf, X, y, cv=3, scoring='accuracy')
    bg_clf_cv_mean.append(scores.mean())
    bg_clf_cv_std.append(scores.std())
    

plt.figure()
# 绘制误差棒图，横轴为num_est，纵轴为scores.mean()，误差为scores.std()
(_, caps, _) = plt.errorbar(num_est, bg_clf_cv_mean, yerr=bg_clf_cv_std, c='blue', fmt='-o', capsize=5)
for cap in caps:
    cap.set_markeredgewidth(1)                                                           
plt.ylabel('Accuracy'); plt.xlabel('Ensemble Size'); plt.title('Bagging Tree Ensemble');
plt.show()

  基于交叉验证的结果，我们可以看到在基分类器数量达到20后，集成的效果不再有明显的提升

随机森林

  随机森林（Random Forest, RF）可以看成是改进的Bagging算法，它可以更好地解决决策树的过拟合问题。随机森林以CART树作为基分类器，对比决策树的Bagging，它有一个明显的特点——随机选择特征，对于普通的决策树，我们会在每个节点在当前的所有特征（假设有n个）中寻找最优特征，而随机森林的决策树会在每个节点在随机选取的特征集合（推荐$n_{rf}={\log }_{2}n$）中寻找最优特征。这样做的好处是如果训练集中的几个特征对输出的结果有很强的预测性，那么这些特征会被每个决策树所应用，这样会导致树之间具有相关性，这样并不会减小模型的方差，但同时随机森林会不可避免的增加偏差。

  RF的主要优点有：

1. 训练可以高度并行化，对于大数据时代的大样本训练速度有优势。个人觉得这是的最主要的优点。

2. 由于可以随机选择决策树节点划分特征，这样在样本特征维度很高的时候，仍然能高效的训练模型。

3. 在训练后，可以给出各个特征对于输出的重要性

4. 由于采用了随机采样，训练出的模型的方差小，泛化能力强。

5. 相对于Boosting系列的Adaboost和GBDT， RF实现比较简单。

6. 对部分特征缺失不敏感。

  RF的主要缺点有：

1. 在某些噪音比较大的样本集上，RF模型容易陷入过拟合。

2. 取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果。

扩展

  RF还有很多变种，其目的都是为了进一步降低方差。

Extremely randomized Trees

  Extremely randomized Trees（以下简称Extra Trees）放弃了Boostrap sampling的方式，而选择使用原始数据集，而且在特征选择时更加暴力的随机选择一个特征直接作为最优特征

*Totally Random Trees Embedding

  参考：http://www.cnblogs.com/pinard/p/6156009.html

  Totally Random Trees Embedding(以下简称 TRTE)是一种非监督学习的数据转化方法。它将低维的数据集映射到高维，从而让映射到高维的数据更好的运用于分类回归模型。我们知道，在支持向量机中运用了核方法来将低维的数据集映射到高维，此处TRTE提供了另外一种方法。

  TRTE在数据转化的过程也使用了类似于RF的方法，建立T个决策树来拟合数据。当决策树建立完毕以后，数据集里的每个数据在T个决策树中叶子节点的位置也定下来了。比如我们有3颗决策树，每个决策树有5个叶子节点，某个数据特征xx划分到第一个决策树的第2个叶子节点，第二个决策树的第3个叶子节点，第三个决策树的第5个叶子节点。则x映射后的特征编码为(0,1,0,0,0, 0,0,1,0,0, 0,0,0,0,1), 有15维的高维特征。这里特征维度之间加上空格是为了强调三颗决策树各自的子编码。

  映射到高维特征后，可以继续使用监督学习的各种分类回归算法了。

*Isolation Forest

  Isolation Forest（以下简称IForest）是一种异常点检测的方法。它也使用了类似于RF的方法来检测异常点。

  对于在T个决策树的样本集，IForest也会对训练集进行随机采样,但是采样个数不需要和RF一样，对于RF，需要采样到采样集样本个数等于训练集个数。但是IForest不需要采样这么多，一般来说，采样个数要远远小于训练集个数？为什么呢？因为我们的目的是异常点检测，只需要部分的样本我们一般就可以将异常点区别出来了。

  对于每一个决策树的建立， IForest采用随机选择一个划分特征，对划分特征随机选择一个划分阈值。这点也和RF不同。

  另外，IForest一般会选择一个比较小的最大决策树深度max_depth,原因同样本采集，用少量的异常点检测一般不需要这么大规模的决策树。

  对于异常点的判断，则是将测试样本点$x$拟合到$T$颗决策树。计算在每颗决策树上该样本的叶子节点的深度$h_t(x)$，从而可以计算出平均高度$h(x)$。此时我们用下面的公式计算样本点xx的异常概率:

$$s(x,m)=2^{-\frac{h(x)}{c(m)}}$$

  其中，m为样本个数。$c(m)$的表达式为：

$$c(m)=2\ln (m-1)+\xi -2\frac{m-1}{m}$$

$\xi$为欧拉常数，$s(x,m)$的取值范围是$[0,1]$，取值越接近于1，则是异常点的概率也越大。

编程（分类）

import time

# DecisionTree
clf3 = DecisionTreeClassifier(criterion='entropy', max_depth=2)

# Tree Bagging
tree_bagging = BaggingClassifier(base_estimator=clf3, n_estimators=100)

# Random Forest
random_forest = RandomForestClassifier(n_estimators=100, criterion='entropy', max_depth = 2)

label = ['Decision Tree', 'Tree Bagging', 'Random Forest']
clf_list = [clf3, tree_bagging, random_forest]

fig = plt.figure(figsize=(15, 4))
gs = gridspec.GridSpec(1, 3)
grid = itertools.product([0], [0, 1, 2])

for clf, label, grd in zip(clf_list, label, grid):
    b = time.time()
    scores = cross_val_score(clf, X, y, cv=3, scoring='accuracy')
    runtime = time.time() - b
    print("Accuracy: %.2f (+/- %.2f) [%s] Runtime: %.2f s" %(scores.mean(), scores.std(), label, runtime))
        
    clf.fit(X, y)
    ax = plt.subplot(gs[grd[0], grd[1]])
    fig = plot_decision_regions(X=X, y=y, clf=clf, legend=2)
    plt.title(label)

plt.show()

Accuracy: 0.63 (+/- 0.04) [Decision Tree] Runtime: 0.01 s
Accuracy: 0.77 (+/- 0.03) [Tree Bagging] Runtime: 0.40 s
Accuracy: 0.76 (+/- 0.04) [Random Forest] Runtime: 0.36 s

  从结果可以看到随机森林的运行速度比Tree Bagging要快一点，这是因为在选择最优特征时，随机森林并没有从全部特征中进行选择

rf_label = ['DecisionTree','1 Trees','5 Trees','10 Trees','20 Trees','100 Trees']

random_forest1 = RandomForestClassifier(n_estimators=1, criterion='entropy', max_depth = 2)
random_forest5 = RandomForestClassifier(n_estimators=5, criterion='entropy', max_depth = 2)
random_forest10 = RandomForestClassifier(n_estimators=10, criterion='entropy', max_depth = 2)
random_forest20 = RandomForestClassifier(n_estimators=20, criterion='entropy', max_depth = 2)
random_forest100 = RandomForestClassifier(n_estimators=100, criterion='entropy', max_depth = 2)

clf_list = [clf3, random_forest1, random_forest5, random_forest10, random_forest20, random_forest100]

fig = plt.figure(figsize=(15, 8))
gs = gridspec.GridSpec(2, 3)
grid = itertools.product([0, 1], [0, 1, 2])

for clf, label, grd in zip(clf_list, rf_label, grid):
    scores = cross_val_score(clf, X, y, cv=3, scoring='accuracy')
    print("Accuracy: %.2f (+/- %.2f) [%s]" %(scores.mean(), scores.std(), label))
        
    clf.fit(X, y)
    ax = plt.subplot(gs[grd[0], grd[1]])
    fig = plot_decision_regions(X=X, y=y, clf=clf, legend=2)
    plt.title(label)

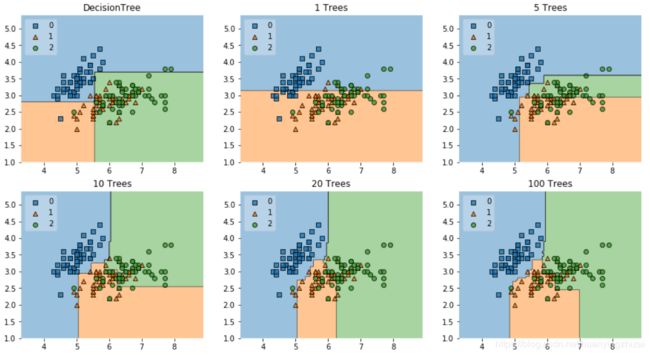
plt.show()

Accuracy: 0.63 (+/- 0.04) [DecisionTree]
Accuracy: 0.59 (+/- 0.08) [1 Trees]
Accuracy: 0.69 (+/- 0.02) [5 Trees]
Accuracy: 0.71 (+/- 0.06) [10 Trees]
Accuracy: 0.74 (+/- 0.04) [20 Trees]
Accuracy: 0.79 (+/- 0.02) [100 Trees]

  可以看到随着树的增加，随机森林的决策边界越来越光滑，精度越来越高。而且当树为1个时随机森林色精度是比决策树要差的，这很容易理解，有可能重要的特征被排除在外了，所以同样是一棵树，随机森林分类效果更差。我们再通过误差棒图看一下决策树数量对精度的影响

num_est = np.concatenate(([1],np.arange(5,105,5)))
rf_clf_cv_mean = []
rf_clf_cv_std = []

for n_est in num_est:    
    rf_clf = RandomForestClassifier(n_estimators=n_est, criterion='entropy', max_depth = 2)
    scores = cross_val_score(rf_clf, X, y, cv=3, scoring='accuracy')
    rf_clf_cv_mean.append(scores.mean())
    rf_clf_cv_std.append(scores.std())
    

plt.figure()
(_, caps, _) = plt.errorbar(num_est, rf_clf_cv_mean, yerr=rf_clf_cv_std, c='blue', fmt='-o', capsize=5)
for cap in caps:
    cap.set_markeredgewidth(1)                                                           
plt.ylabel('Accuracy')
plt.xlabel('Trees Number')
plt.show()

  可以看到随着树的数量增加，随机森林一开始有明显的提升，但是当树到达10个后就基本趋于稳定了

  下面我们比较一下随着学习器的增加，Tree Bagging和Random Forest的差异

num_est = np.concatenate(([1],np.arange(10,1005,10)))
bg_arr = []
rf_arr = []

for n_est in num_est:    
    rf_clf = RandomForestClassifier(n_estimators=n_est, criterion='entropy', max_depth = 2)
    rf_scores = cross_val_score(rf_clf, X, y, cv=3, scoring='accuracy')
    rf_arr.append(rf_scores.mean())
    
    bg_clf = BaggingClassifier(base_estimator=clf3, n_estimators=n_est, max_samples=0.8, max_features=0.8)
    bg_scores = cross_val_score(bg_clf, X, y, cv=3, scoring='accuracy')
    bg_arr.append(bg_scores.mean())
    

plt.figure()
plt.plot(num_est, bg_arr,  color='blue', label='Bagging')
plt.plot(num_est, rf_arr, color='red', label='Random Forest')
plt.legend()
plt.ylabel('Accuracy')
plt.xlabel('Learner Number')
plt.show()

  可以看到Bagging和随机森林有相似的收敛性，但是随着个体学习器数量的增加，随机森林的泛化性能要更好。

为什么说Bagging通过减小方差来提升精度

  因为Bagging是同质集成并且数据集也相同，因此各个学习器的偏差$bias(h_t(x))$和方差$Var(h_t(x))$近似相等，但是各个学习器并不是独立的，于是
$$bias(H(x))=bias\left(\frac{1}{T}\sum _{t=1}^T{h}_t(x)\right)=bias(h_t(x))$$

$$Var(H(x))=Var\left(\frac{1}{T}\sum _{t=1}^T{h}_t(x)\right)=\frac{1}{T}Var(h_t(x))$$

所以Bagging不能降低偏差，而是会降低方差（因为学习器之间的相关性，方差不会下降到$\frac{1}{T}Var(h_t(x))$），如果各个学习器完全相同，即有$\frac{1}{T}{\sum }_{t=1}^T{h}_t(x)=h_t(x)$，那么方差也不会降低，这也就是为什么要求学习器之间要有“多样性”。随机森林通过随机选取特征的方式降低了各决策树的相关性，使得方差进一步降低。

Boosting

  不同于bagging方法，boosting方法通过分步迭代（stage-wise）的方式来构建模型，在迭代的每一步构建的弱学习器都是为了弥补已有模型的不足。Boosting算法先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至基学习器数目达到事先指定的值T，最终将这T个基学习器进行加权。从偏差—方差分解的角度看，Boosting主要关注降低偏差，因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成。下图以Adaboost分类为例简要说明了Boosting的机制

Adaboost

  Boosting算法最著名的代表是Adaboost（Adaptive Boosting）算法。Adaboost不改变所给的训练数据，而不断改变训练数据的权值分布，使得训练数据在基本分类器的学习中起不同的作用，然后利用基本分类器的线性组合构建最终的分类器。Adaboost的二类分类算法的描述如下图所示，其中 $y_i\in \{-1,+1\}$，$i=1,2,...,m$，$f$是真实函数，${\mathcal{D}}_t$是调整后用于进行第$t$次训练的样本分布，$h_t$ 是基于分布${\mathcal{D}}_t$从数据集$D$中训练出的分类器，${ϵ}_t$是$h_t$误差的估计，${\alpha }_t$是分类器$h_t$的权重，$Z_t$是规范化因子，以确保${\mathcal{D}}_{t+1}$是一个分布，$t=1,2,...,T$。

  Adaboost是一种比较有特点的算法，可以总结如下：

1. 每次迭代改变的是样本的分布，而不是重复采样（re weight)。

2. 样本分布的改变取决于样本是否被正确分类：总是分类正确的样本权值低，总是分类错误的样本权值高（通常是边界附近的样本）。

3. 最终的结果是弱分类器的加权组合，权值表示该弱分类器的性能。

  我们通过一个例子来感受一下Adaboost的机制

实例

  我们有如下数据集，其中有红色圆形和绿色三角形共10个样本，希望建立一个分类器，能判断出任意位置样本属于哪一类，我们指定基学习器个数$T$为3

  我们初始化样本权值分布${\mathcal{D}}_1=0.1,0.1,\cdots ,0.1$，并基于该分布从训练集中训练出分类器$h_1$（理论上$h_1$应使分类错误率达到最小，这里仅用一条线代表分类结果，并未给出这条线是怎么得到的，但是不代表这条线是随意做出的），之后估计$h_1$的误差${ϵ}_1$，确定$h_1$的权重${\alpha }_1$，并更新样本的权值分布

  重复上面操作依次训练出基学习器$h_2$、$h_3$，此时基学习器个数达到我们预先指定的值。可以按照基学习器的权重给出输出公式。并据此预测其他样本的分类

  每个区域是属于哪个类别，由这个区域所在分类器的权值综合决定。比如左下角的区域的样本，属于绿色分类区的权重为$h_1$中的0.42和$h_2$ 中的0.65，其和为1.07；属于红色分类区域的权重为$h_3$中的0.92；属于红色分类区的权重小于属于绿色分类区的权值，因此左下角属于绿

  从结果中看，即使简单的分类器，组合起来也能获得很好的分类效果。

模型推导

  Adaboost算法有多种推导方式，一种比较容易理解的是基于“加性模型”，即基学习器的线性组合

$$H(x)=\sum _{t=1}^T{\alpha }_t{h}_t(x)$$

来最小化指数损失函数

$$Loss(H|\mathcal{D})={\mathbb{E}}_{\mathcal{D}}[e^{-yH(x)}]=e^{-H(x)}P(y=1|x)+e^{H(x)}P(y=-1|x)$$

---

●什么是前向分步算法（forward stagewise algorithm）？

  前向分步算法是求解加法模型损失函数（${\sum }_{i=1}^{N}Loss(y_i,\alpha h(x_i))$）最小化的一种算法，简单来说就是在每一次学习一个基学习器，然后逐步逼近目标函数：

$$\begin{array}{lclcc}{f}_0(x)& =& 0& & \\ f_1(x)& =& f_0(x)+{\alpha }_1{h}_1(x)& =& {\alpha }_1{h}_1(x)\\ f_2(x)& =& f_1(x)+{\alpha }_2{h}_2(x)& =& {\alpha }_1{h}_1(x)+{\alpha }_2{h}_2(x)\\ \cdots & & & & \\ f_M(x)& =& f_{M-1}(x)+{\alpha }_M{h}_M(x)& =& {\sum }_{m=1}^M{\alpha }_m{h}_m(x)\end{array}$$

---

●为什么是指数损失函数？

  指数损失函数对$H(x)$求偏导得

$$\frac{\partial Loss(H|\mathcal{D})}{\partial H(x)}=-e^{-H(x)}P(y=1|x)+e^{H(x)}P(y=-1|x)$$

令偏导数为0有

$$H(x)=\frac{1}{2}\ln \frac{P(y=1|x)}{P(y=-1|x)}$$

于是有

$$\begin{array}{rl}sign\left(H(x)\right)& =sign\left(\frac{1}{2}\ln \frac{P(y=1|x)}{P(y=-1|x)}\right)\\ & =\{\begin{array}{ll}0& \text{if }P(y=1|x)>P(y=-1|x)\\ 1& \text{if }P(y=1|x)<P(y=-1|x)\end{array}\\ & ={\mathrm{argmax}}_{y\in \{+1,-1\}}P(y|x)\end{array}$$

过程中忽略了$P(y=1|x)=P(y=-1|x)$的情况，另外西瓜书中对于概率的写法是$P(f(x)=y|x)$，其中$f$是真实函数。从结果可知，$sign\left(H(x)\right)$达到了贝叶斯最优错误率（$ifP({\omega }_1|x)>P({\omega }_1|x),thenx\in {\omega }_1,elsex\in {\omega }_2$），即最小化指数损失函数等价于分类错误率最小化。因此我们可以用它替代0/1损失函数作为最优目标。有了以上结论，我们便可以进行算法的推导。

---

●推导过程

  在算法的第$t$次循环中，我们基于分布${\mathcal{D}}_t$产生了基分类器$h_t(x)$和分类器权重${\alpha }_t$，那么它们应该使得$H_t(x)={\sum }_{k=1}^t{\alpha }_k{h}_k(x)$最小化损失函数

$$\begin{array}{rl}Loss(H_t(x)|{\mathcal{D}}_t)& =Loss(\sum _{k=1}^t{\alpha }_k{h}_k(x)|{\mathcal{D}}_k)\\ & =Loss(H_{t-1}(x)+{\alpha }_t{h}_t(x)|{\mathcal{D}}_k)\\ & ={\mathbb{E}}_{{\mathcal{D}}_t}{e}^{-y(H_{t-1}(x)+{\alpha }_t{h}_t(x))}\\ & =\sum _{i=1}^N{e}^{-y_i{H}_{t-1}(x_i)}{e}^{-y_i{\alpha }_t{h}_t(x_i)}\end{array}$$

我们令$w_{t,i}=e^{-y_i{H}_{t-1}(x_i)}$，显然，$w_{t,i}$与${\alpha }_t$和$h_t$无关，所以与最小化损失也无关，于是有

$$Loss(H_t(x)|{\mathcal{D}}_t)=\sum _{i=1}^N{w}_{t,i}{e}^{-y_i{\alpha }_t{h}_t(x_i)}$$

设$h_t^{\ast }$和${\alpha }_t^{\ast }$是满足要求的分类器和分类器权重，即

$$(h_t^{\ast },{\alpha }_t^{\ast })={\mathrm{argmin}}_{{\alpha }_t,h_t}Loss(H_t(x)|{\mathcal{D}}_t)={\mathrm{argmin}}_{{\alpha }_t,h_t}\sum _{i=1}^N{w}_{t,i}{e}^{-y_i{\alpha }_t{h}_t(x_i)}$$

对任意${\alpha }_t>0$，考虑

$$h_t^{\ast }(x)={\mathrm{argmin}}_{h_t}\sum _{i=1}^N{w}_{t,i}I(h_t(x_i)̸=y_i)$$

这意味着$h_t^{\ast }(x)$是使第t轮加权训练数据分类误差最小的基本分类器，即为所求。再求${\alpha }_t^{\ast }$

$$Loss(H_t(x)|{\mathcal{D}}_t)=\sum _{i=1}^N{w}_{t,i}{e}^{-y_i{\alpha }_t{h}_t^{\ast }(x_i)}=\sum _{h_t^{\ast }(x_i)̸=y_i}{w}_{t,i}{e}^{{\alpha }_t}+\sum _{h_t^{\ast }(x_i)=y_i}{w}_{t,i}{e}^{-{\alpha }_t}$$

损失函数对${\alpha }_t$求偏导得

$$\frac{\partial Loss(H_t(x)|{\mathcal{D}}_t)}{\partial {\alpha }_t}=-\sum _{h_t^{\ast }(x_i)̸=y_i}{w}_{t,i}{e}^{{\alpha }_t}+\sum _{h_t^{\ast }(x_i)=y_i}{w}_{t,i}{e}^{-{\alpha }_t}$$

令偏导数为0有

$${\alpha }_t^{\ast }=\frac{1}{2}\ln \frac{1-{\sum }_{h_t^{\ast }(x_i)̸=y_i}{w}_{t,i}}{{\sum }_{h_t^{\ast }(x_i)̸=y_i}{w}_{t,i}}=\frac{1}{2}\ln \frac{1-{ϵ}_t}{{ϵ}_t}$$

再来看样本权值的更新，$H_t(x_i)=H_{t-1}(x_i)+{\alpha }_t{h}_t(x_i)$两边同时乘$-y_i$并进行指数运算得

$$w_{t+1,i}=e^{-y_i{H}_t(x_i)}=e^{-y_i{H}_{t-1}(x_i)}{e}^{-y_i{\alpha }_t{h}_t(x_i)}=w_{t,i}{e}^{-y_i{\alpha }_t{h}_t(x_i)}$$

之后为确保${\mathcal{D}}_{t+1}$是一个分布，再对权值进行规范化即可

为什么说Boosting通过减小偏差来提升精度

  Boosting算法等价于用前向分步算法来最小化损失函数，以Adaboost为例，算法用这样的方式顺序地最小化指数损失函数$Loss(y,H_t(x))$，偏差自然降低。但也正是因为这样造成了子模型之间的强相关性，因此不能显著降低方差。所以所Boosting主要通过降低偏差来提升精度

*多分类任务

参考：https://blog.51cto.com/baidutech/743809

  目前比较常用的多分类方法有三种

adaboost M1方法

  该方法的主要思路是利用多分类的基学习器，最终选择最有可能的分类结果

$$H(x)={\mathrm{argmax}}_{y\in \mathcal{Y}}\sum _{t:h_t(x)=y}{\alpha }_t$$

adaboost MH方法

  应用“one-vs-all”的原理重构样本空间，最终选择最有可能的结果

对多分类输出进行二进制编码

  类似adaboost MH方法，不过不需要重构样本空间，而是把Label映射到$K$位的二进制码上（$K$位分类数），然后训练$K$个二分类分类器，在解码时生成$K$位的二进制数。从而对应到一个label上。

编程（分类）

  仍然使用Iris数据集，决策树算法作为个体学习器算法

import itertools
import numpy as np

import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec

from sklearn import datasets

from sklearn.tree import DecisionTreeClassifier

from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import cross_val_score, train_test_split

from mlxtend.plotting import plot_learning_curves
from mlxtend.plotting import plot_decision_regions

iris = datasets.load_iris()
X, y = iris.data[:, 0:2], iris.target
    
clf = DecisionTreeClassifier(criterion='entropy', max_depth=2)

num_est = [1, 2, 3, 10]
label = ['AdaBoost (n_est=1)', 'AdaBoost (n_est=2)', 'AdaBoost (n_est=3)', 'AdaBoost (n_est=10)']

fig = plt.figure(figsize=(10, 8))
gs = gridspec.GridSpec(2, 2)
grid = itertools.product([0,1],repeat=2)

for n_est, label, grd in zip(num_est, label, grid):     
    boosting = AdaBoostClassifier(base_estimator=clf, n_estimators=n_est)  
    
    scores = cross_val_score(boosting, X, y, cv=3, scoring='accuracy')
    print("Accuracy: %.2f (+/- %.2f) [%s]" %(scores.mean(), scores.std(), label))
    
    boosting.fit(X, y)
    ax = plt.subplot(gs[grd[0], grd[1]])
    fig = plot_decision_regions(X=X, y=y, clf=boosting, legend=2)
    plt.title(label)

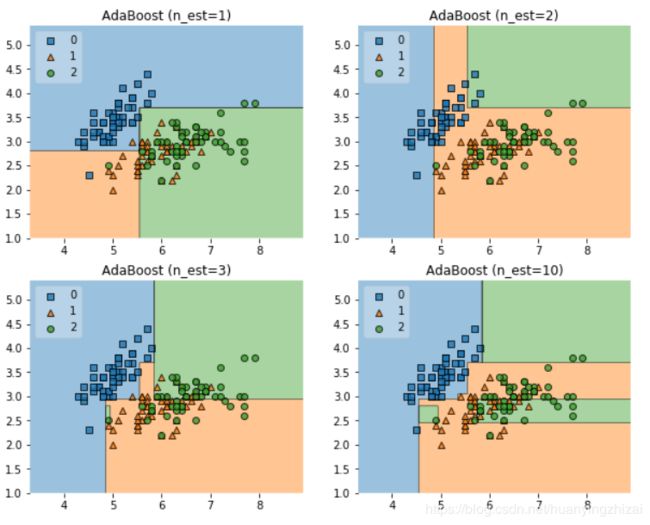
plt.show()

Accuracy: 0.63 (+/- 0.04) [AdaBoost (n_est=1)]
Accuracy: 0.56 (+/- 0.11) [AdaBoost (n_est=2)]
Accuracy: 0.73 (+/- 0.04) [AdaBoost (n_est=3)]
Accuracy: 0.71 (+/- 0.08) [AdaBoost (n_est=10)]

  再来看看不同训练计划分下Adaboost的表现

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

boosting = AdaBoostClassifier(base_estimator=clf, n_estimators=10)
        
plt.figure()
plot_learning_curves(X_train, y_train, X_test, y_test, boosting, print_model=False, style='ggplot')
plt.show()

  下面是不同基学习器个数下的Adaboost的精度

#Ensemble Size
num_est = np.concatenate(([1],np.arange(5,105,5)))
ada_clf_cv_mean = []
ada_clf_cv_std = []

for n_est in num_est:
    ada_clf = AdaBoostClassifier(base_estimator=clf, n_estimators=n_est)
    scores = cross_val_score(ada_clf, X, y, cv=3, scoring='accuracy')
    ada_clf_cv_mean.append(scores.mean())
    ada_clf_cv_std.append(scores.std())
    


plt.figure()
(_, caps, _) = plt.errorbar(num_est, ada_clf_cv_mean, yerr=ada_clf_cv_std, c='blue', fmt='-o', capsize=5)
for cap in caps:
    cap.set_markeredgewidth(1)                                                                        
plt.ylabel('Accuracy'); plt.xlabel('Ensemble Size'); plt.title('AdaBoost Ensemble');
plt.show()

  运行过程中我们可以明显的发现其和Bagging与RF的不同，就是一旦参数确定了结果就是一定的，没有随机性。这是因为Bagging采样的随机性和RF特征选择的随机性。我们再来比较一下这三个模型的精度随着基学习数目增加精度的变化。

num_est = np.concatenate(([1],np.arange(10,100,10),np.arange(100,1001,50)))
bg_arr = []
rf_arr = []
ada_arr = []

for n_est in num_est:    
    rf_clf = RandomForestClassifier(n_estimators=n_est, criterion='entropy', max_depth = 2)
    rf_scores = cross_val_score(rf_clf, X, y, cv=3, scoring='accuracy')
    rf_arr.append(rf_scores.mean())
    
    bg_clf = BaggingClassifier(base_estimator=clf, n_estimators=n_est, max_samples=0.8, max_features=0.8)
    bg_scores = cross_val_score(bg_clf, X, y, cv=3, scoring='accuracy')
    bg_arr.append(bg_scores.mean())
    
    ada_clf = AdaBoostClassifier(base_estimator=clf, n_estimators=n_est)
    scores = cross_val_score(ada_clf, X, y, cv=3, scoring='accuracy')
    ada_arr.append(scores.mean())
    

plt.figure()
plt.plot(num_est, bg_arr,  color='blue', label='Bagging')
plt.plot(num_est, rf_arr, color='red', label='Random Forest')
plt.plot(num_est, ada_arr, color='green', label='Adaboost')
plt.legend()
plt.ylabel('Accuracy')
plt.xlabel('Learner Number')
plt.show()

  可见以决策树为基学习器的Adaboost模型表现并不是很好

*训练误差分析

  Adaboost最基本的性质是它能在学习过程中不断减少训练误差，下面我们来证明这一性质。我们先令$g(x)={\sum }_{t=1}T{\alpha }_t{h}_t(x)$，令$w_{t,i}$表示第$t$轮中样本$i$的权值，显然有$w_{1,i}=\frac{1}{N}$，则Adaboost最终分类器$H(x)$的训练误差界为：

$$bias(H(x))=\frac{1}{N}\sum _{i=1}^{N}I(H(x_i)̸=y_i)\le \frac{1}{N}\sum _{i=1}^N{e}^{-y_{i}g(x_i)}=\prod _{t=1}^T{Z}_t$$

  证明：

  当$H(x_i)̸=y_i$时，$y_{i}g(x_i)<0$，所以$e^{-y_{i}g(x_i)}>1=I(H(x_i)̸=y_i)$，于是不等式的前半部分得证，下面只需证明$\frac{1}{N}{\sum }_{i=1}^N{e}^{-y_{i}g(x_i)}={\prod }_{t=1}^T{Z}_t$：

$$\begin{array}{rl}\frac{1}{N}\sum _{i=1}^N{e}^{-y_{i}g(x_i)}& =\frac{1}{N}\sum _{i=1}^N{e}^{-y_i{\sum }_{t=1}^T{\alpha }_t{h}_t(x_i)}\\ & =w_{1,i}\sum _{i=1}^N{e}^{-{\sum }_{t=1}^T{\alpha }_t{h}_t(x_i)y_i}\\ & =\sum _{i=1}^N{w}_{1,i}\prod _{t=1}^T{e}^{-{\alpha }_t{h}_t(x_i)y_i}\\ & =Z_1\sum _{i=1}^N\frac{w_{1,i}{\prod }_{t=1}^T{e}^{-{\alpha }_t{h}_t(x_i)y_i}}{Z_1}\\ & =Z_1\sum _{i=1}^N{w}_{2,i}\prod _{t=2}^T{e}^{-{\alpha }_t{h}_t(x_i)y_i}\\ & =Z_1{Z}_2\sum _{i=1}^N{w}_{3,i}\prod _{t=3}^T{e}^{-{\alpha }_t{h}_t(x_i)y_i}\\ & =\cdots \\ & =Z_1{Z}_2\cdots Z_{t-1}\sum _{i=1}^N{w}_{T,i}{e}^{-{\alpha }_T{h}_T(x_i)y_i}\\ & =\prod _{t=1}^T{Z}_t\end{array}$$

■ 

  通过这个定理，我们可以在每一轮都适当修改$H_t$使得$Z_t$最小，从而使训练误差下降最快。特别的，对于二分类问题，我们有以下结论：

$$\prod _{t=1}^T{Z}_t=\prod _{t=1}^T[2\sqrt{{ϵ}_t(1-{ϵ}_t)}=\prod _{t=1}^T\sqrt{(1-4{\gamma }_t^2)}\le exp\left(-2\sum _{t=1}^T{\gamma }_t^2\right)$$

其中，${\gamma }_t=\frac{1}{2}-{ϵ}_t>0$

  证明：

  先证明等式的部分：

$$\begin{array}{rl}{Z}_t& =\sum _{i=1}^N{w}_{t,i}exp(-{\alpha }_t{y}_i{h}_t(x_i))\\ & =\sum _{y_i=h_t(x_i)}{w}_{t,i}{e}^{-{\alpha }_t}+\sum _{y_i̸=h_t(x_i)}{w}_{t,i}{e}^{{\alpha }_t}\\ & =e^{-{\alpha }_t}\sum _{y_i=h_t(x_i)}{w}_{t,i}+e^{{\alpha }_t}\sum _{y_i̸=h_t(x_i)}{w}_{t,i}\\ & =e^{-{\alpha }_t}(1-{ϵ}_t)+e^{{\alpha }_t}{ϵ}_t\\ & ={\left(\frac{1-{ϵ}_t}{{ϵ}_t}\right)}^{-\frac{1}{2}}(1-{ϵ}_t)+{\left(\frac{1-{ϵ}_t}{{ϵ}_t}\right)}^{\frac{1}{2}}{ϵ}_t\\ & =2\sqrt{{ϵ}_t(1-{ϵ}_t)}\\ & =\prod _{t=1}^T\sqrt{(1-4{\gamma }_t^2)}\end{array}$$

  不等式部分可由$\sqrt{1-x}$和$e^x$在$x=0$处的泰勒展开式推导得出

■ 

  进一步，若存在$\gamma >0$使得对所有$t$有${\gamma }_t\ge \gamma$，那么有：

$$bias(H(x))\le exp\left(-2T{\gamma }^2\right)$$

  这表明Adaboost在这种条件下的训练误差是以指数速率下降的

*过拟合分析

  这里仅给出结论——Adaboost不会发生过拟合，这是Adaboost的另一个性质。“margin theory”可以比较直观地解释这一性质。

总结

  ●优点

1. adaboost是一种有很高精度的分类器。

2. 可以使用各种方法构建子分类器，adaboost算法提供的是框架。

3. 当使用简单分类器时，计算出的结果是可以理解的。而且弱分类器构造极其简单。

4. 简单，不用做特征筛选。

5. 不用担心overfitting！

6. 随着迭代次数的增加，实际上错误率上界在下降。

  ●缺点

1. 对异常值非常敏感

2. 对损失函数形式有要求

  ●应用

1. 用于二分类或多分类的应用场景

2. 用于做分类任务的baseline

3. 用于特征选择（feature selection)

4. 用于修正badcase，

提升树

  提升树（Boosting Tree）是以二叉分类树或二叉回归树为基本分类器的提升方法，采用加法模型（即基函数的线性组合）与前向分步算法。提升树有很多不同的算法，其主要区别在于使用的损失函数不同，包括用平方误差损失函数的回归问题，用指数函数损失的分类问题，以及用一般损失函数的一般决策问题。

  提升树模型为：

$$f_M(x)=\sum _{m=1}^{M}T(x;{\Theta }_m)$$

其中$T(x;{\Theta }_m)$为决策树；${\Theta }_m$为决策树的参数；$M$为树的个数。首先确定初始模型：

$$f_0(x)=0$$

第$m$步的模型是：

$$f_m(x)=f_{m-1}(x)+T(x;{\Theta }_m),m=1,2,\cdots ,M$$

通过最小化损失函数确定决策树$T(x;{\Theta }_m)$的参数：

$${\hat{\Theta }}_m={\mathrm{argmin}}_{{\Theta }_m}Loss(y,f_m(x))={\mathrm{argmin}}_{{\Theta }_m}Loss(y,f_{m-1}(x)+T(x;{\Theta }_m))$$

  以回归问题的提升树为例，其损失函数是平方误差损失

$$\begin{array}{rl}Loss(y,f_m(x))& =Loss(y,f_{m-1}(x)+T(x;{\Theta }_m))\\ & ={(y-f_{m-1}(x)-T(x;{\Theta }_m))}^2\\ & ={(r_m-T(x;{\Theta }_m))}^2\end{array}$$

其中，$r_m$是当前模型拟合数据的残差，因此我们只需根据$(x,r_m)$来学习一个回归树$T(x;{\Theta }_m)$，进而确定$f_m(x)=f_{m-1}(x)+T(x;{\Theta }_m)$，最终学得$f_M(x)={\sum }_{m=1}^{M}T(x;{\Theta }_m)$

实例

  考虑用如下数据集学习一个提升树模型（深度为1）

$x_i$	1	2	3	4	5	6	7
$y_i$	4.5	4.7	4.9	5.3	5.8	7.0	7.9

  解 第1步求$f_1(x)$即回归树$T(x;{\Theta }_1)$

根据已知的数据，我们可以考虑如下切分点：

$$1.5,2.5,3.5,4.5,5.5,6.5$$

回忆二叉回归树的解法，容易求出各切分点$s$下

$$g(s)={\min }_{c_1}\sum _{x\in R_1}{(y_i-c_1)}^2+{\min }_{c_2}\sum _{x\in R_2}{(y_i-c_2)}^2$$

其中$R_1=\{x\le s\}$，$R_2=\{x>s\}$，$c_1$、$c_2$易知为$c_1=\bar{y}I(x\in R_1)$，$c_2=\bar{y}I(x\in R_2)$

当$s=1.5$时，$c_1=4.5$，$c_2=(4.7+4.9+5.3+5.8+7+7.9)/6=5.93$，$g(s)=0+(4.7-5.93{)}^2+(4.9-5.93{)}^2+(5.3-5.93{)}^2+(5.8-5.93{)}^2+(7-5.93{)}^2+(7.9-5.93{)}^2=8.0134$

当$s=2.5$时，$c_1=(4.5+4.7)/2=4.6$，$c_2=(4.9+5.3+5.8+7+7.9)/5=6.18$，$g(s)=(4.5-4.6{)}^2+(4.7-4.6{)}^2+(4.9-6.18{)}^2+(5.3-6.18{)}^2+(5.8-6.18{)}^2+(7-6.18{)}^2+(7.9-6.18{)}^2=6.208$

当$s=3.5$时，$c_1=(4.5+4.7+4.9)/3=4.7$，$c_2=(5.3+5.8+7+7.9)/4=6.5$，$g(s)=(4.5-4.7{)}^2+(4.7-4.7{)}^2+(4.9-4.7{)}^2+(5.3-6.5{)}^2+(5.8-6.5{)}^2+(7-6.5{)}^2+(7.9-6.5{)}^2=4.22$

当$s=4.5$时，$c_1=(4.5+4.7+4.9+5.3)/4=4.85$，$c_2=(5.8+7+7.9)/3=6.90$，$g(s)=(4.5-4.85{)}^2+(4.7-4.85{)}^2+(4.9-4.85{)}^2+(5.3-4.85{)}^2+(5.8-6.9{)}^2+(7-6.9{)}^2+(7.9-6.9{)}^2=2.57$

当$s=5.5$时，$c_1=(4.5+4.7+4.9+5.3+5.8)/5=5.04$，$c_2=(7+7.9)/2=7.45$，$g(s)=(4.5-5.04{)}^2+(4.7-5.04{)}^2+(4.9-5.04{)}^2+(5.3-5.04{)}^2+(5.8-5.04{)}^2+(7-7.45{)}^2+(7.9-7.45{)}^2=1.477$

当$s=6.5$时，$c_1=(4.5+4.7+4.9+5.3+5.8+7)/6=5.37$，$c_2=7.9$，$g(s)=(4.5-5.37{)}^2+(4.7-5.37{)}^2+(4.9-5.37{)}^2+(5.3-5.37{)}^2+(5.8-5.37{)}^2+(7-5.37{)}^2+0=4.2734$

$s$	1.5	2.5	3.5	4.5	5.5	6.5
$g(s)$	8.01	6.21	4.22	2.57	1.48	4.27

所以切分点$s$应为5.5，即

$$T_1(x)=\{\begin{array}{ll}5.04,& x\le 5.5\\ 7.45,& x>5.5\end{array}$$

于是$f_1(x)=T_1(x)$

用$f_1(x)$拟合训练数据的平方损失为

$$Loss(y,f_1(x))=\sum _{i=1}^7{(y_i-f_1(x_i))}^2=1.477$$

下面用$f_1(x)$拟合残差$r_{2,i}=y_i-f_1(x_i)$：

$x_i$	1	2	3	4	5	6	7
$r_{2,i}$	-0.54	-0.34	-0.14	0.26	0.76	-0.45	0.45

接着求$T_2(x)$，方法同求$T_1(x)$，得

$s$	1.5	2.5	3.5	4.5	5.5	6.5
$g(s)$	1.14	0.92	0.87	1.14	1.48	1.24

所以切分点为3.5，即

$$T_2(x)=\{\begin{array}{ll}-0.34,& x\le 3.5\\ 0.255,& x>3.5\end{array}$$

于是$f_2(x)=f_1(x)+T_2(x)$，有

$$f_2(x)=\{\begin{array}{ll}4.7,& x\le 3.5\\ 5.295,& 3.5<x\le 5.5\\ 7.705,& x>5.5\end{array}$$

用$f_2(x)$拟合训练数据的平方损失为

$$Loss(y,f_2(x))=\sum _{i=1}^7{(y_i-f_2(x_i))}^2=0.870$$

假设我们提前设定决策树的数量就是2，那么$f_2(x)$即为所求，否则继续重复前面的运算直到决策树数量达到预先设定值$M$或者$f_m(x)$拟合训练数据的平方误差损失满足要求

梯度提升

  梯度提升（Gradient boosting）是一种用于回归、分类和排序任务的机器学习技术，属于Boosting算法族的一部分。梯度提升通过集成多个弱学习器，通常是决策树，来构建最终的预测模型，在提升树的基础上，当损失函数不能使用便于计算的平方损失或者指数损失时，利用损失函数的负梯度

$$-{\left[\frac{\partial Loss(y,f(x_i))}{\partial f(x_i}\right]}_{f(x)=f_{m-1}(x)}$$

作为回归问题提升树算法中的残差的近似值，即

$$r_{m,i}=-{\left[\frac{\partial Loss(y,f(x_i))}{\partial f(x_i}\right]}_{f(x)=f_{m-1}(x)}$$

GBDT

  参考：https://www.zybuluo.com/yxd/note/611571#gbdt算法

  基于梯度提升算法的学习器叫做GBM(Gradient Boosting Machine)。理论上，GBM可以选择各种不同的学习算法作为基学习器。现实中，用得最多的基学习器是决策树。为什么梯度提升方法倾向于选择决策树（通常是CART树）作为基学习器呢？这与决策树算法自身的优点有很大的关系。决策树可以认为是if-then规则的集合，易于理解，可解释性强，预测速度快。同时，决策树算法相比于其他的算法需要更少的特征工程，比如可以不用做特征标准化，可以很好的处理字段缺失的数据，也可以不用关心特征间是否相互依赖等。决策树能够自动组合多个特征，学习特征之间更高级别的相互关系，它可以毫无压力地处理特征间的交互关系并且是非参数化的，因此你不必担心异常值或者数据是否线性可分（举个例子，决策树能轻松处理好类别A在某个特征维度x的末端，类别B在中间，然后类别A又出现在特征维度x前端的情况）。此外，模型很容易实现扩展。不过，单独使用决策树算法时，有容易过拟合缺点。所幸的是，通过各种方法，抑制决策树的复杂性，降低单颗决策树的拟合能力，再通过梯度提升的方法集成多个决策树，最终能够很好的解决过拟合的问题。由此可见，梯度提升方法和决策树学习算法可以互相取长补短，是一对完美的搭档。至于抑制单颗决策树的复杂度的方法有很多，比如限制树的最大深度、限制叶子节点的最少样本数量、限制节点分裂时的最少样本数量、吸收bagging的思想对训练样本采样（subsample），在学习单颗决策树时只使用一部分训练样本、借鉴随机森林的思路在学习单颗决策树时只采样一部分特征、在目标函数中添加正则项惩罚复杂的树结构（XGboost）等。现在主流的GBDT算法实现中这些方法基本上都有实现，因此GBDT算法的超参数还是比较多的，应用过程中需要精心调参，并用交叉验证的方法选择最佳参数。

  具体的算法如下：

---

  输入：训练数据集$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$，$x_i\in \mathcal{X}\subseteq {\mathbb{R}}^n$，$y_i\in \mathcal{Y}\subseteq \mathbb{R}$；损失函数$Loss(y,f(x))$；

  输出：回归树$\hat{f}(x)$

  (1) 初始化

$$f_0(x)={\mathrm{argmin}}_c\sum _{i=1}^{N}Loss(y_i,c)$$

  (2) For $m=1,2,\cdots ,M$ do:

    (a) 计算

$$r_{m,i}=-{\left[\frac{\partial Loss(y,f(x_i))}{\partial f(x_i}\right]}_{f(x)=f_{m-1}(x)}$$

    (b) 对(x_i, r_{m,i})拟合一个回归树，得到第m棵树的叶节点区域$R_{m,j}$，$j=1,2,\cdots ,J$

    © 对$j=1,2,\cdots ,J$，计算

$$c_{m,j}={\mathrm{argmin}}_c\sum _{x_i\in R_{m,j}}Loss(y_i,f_{m-1}+c)$$

    (d) 更新$f_m(x)=f_{m-1}(x)+{\sum }_{j=1}^J{c}_{m,j}I(x\in R_{m,j})$

  (3) 得到回归树

$$\hat{f}(x)=f_M(x)=\sum _{m=1}^M\sum _{j=1}^J{c}_{m,j}I(x\in R_{m,j})$$

---

GBDT实例

  我们仍以前面的例子为例，损失函数也仍然选择平方误差损失，我们看看结果是否会有不同

  解  第一步先初始化$f_0(x)$，易知使平方误差损失达到最小的$c$值为$c_0=\frac{1}{7}{\sum }_{i=1}^7{y}_i=5.73$，于是$f_0(x)=c_0=5.73$

接着拟合第一轮的残差

$$r_{1,i}=-{\left[\frac{\partial Loss(y_i,f(x_i))}{\partial f(x_i)}\right]}_{f_0(x)}=2{[y_i-f(x_i)]}_{f_0(x)}$$

于是有

$x_i$	1	2	3	4	5	6	7
$r_{1,i}$	-2.45	-2.06	-1.66	-0.86	0.14	2.54	4.34

对$r_{1,i}$拟合回归树，易求得各切分点下的$g(s)$为

$s$	1.5	2.5	3.5	4.5	5.5	6.5
$g(s)$	32.05	24.80	16.87	10.26	5.89	17.06

于是确定切分点$s=5.5$，叶节点区域$R_{1,1}=\{x|x\le 5.5\}$，$R_{1,2}=\{x|x>5.5\}$，有回归树

$$T_1(x)=\{\begin{array}{ll}-1.38,& x\le 5.5\\ 3.44,& x>5.5\end{array}$$

进而有

$$c_{1,1}=\frac{1}{5}\sum _{i=1}^5[y_i-f_0(x_i)]=\frac{1}{5}\sum _{i=1}^5{y}_i-f_0(x)=-0.69$$

$$c_{1,2}=\frac{1}{2}\sum _{i=6,7}[y_i-f_0(x_i)]=\frac{1}{5}\sum _{i=6,7}{y}_i-f_0(x)=1.72$$

最后学得

$$f_1(x)=f_0(x)+\sum _{j=1}^2{c}_{1,j}I(x\in R_{1,j})=\{\begin{array}{ll}5.04,& x\le 5.5\\ 7.45,& x>5.5\end{array}$$

用$f_1(x)$拟合训练数据的平方损失误差：

$$Loss(y,f_1(x))=\sum _{i=1}^7{[y_i-f_1(x_i)]}^2=1.477$$

至此我们可以看到虽然学习过程不同，但是学得的$f_1(x)$和提升树是相同的，那么继续下一轮的学习，计算

$$r_{2,i}=-{\left[\frac{\partial Loss(y_i,f(x_i))}{\partial f(x_i)}\right]}_{f_1(x)}=2{[y_i-f(x_i)]}_{f_1(x)}$$

于是有

$x_i$	1	2	3	4	5	6	7
$r_{2,i}$	-1.08	-0.68	-0.28	0.52	1.52	-0.9	0.9

对$r_{2,i}$拟合回归树，易求得各切分点下的$g(s)$为

$s$	1.5	2.5	3.5	4.5	5.5	6.5
$g(s)$	4.55	3.74	3.48	4.56	5.89	4.96

于是确定切分点$s=3.5$，叶节点区域$R_{2,1}=\{x|x\le 3.5\}$，$R_{2,2}=\{x|x>3.5\}$，有回归树

$$T_1(x)=\{\begin{array}{ll}-0.68,& x\le 3.5\\ 0.51,& x>3.5\end{array}$$

进而有

$$c_{2,1}=\frac{1}{3}\sum _{i=1}^3[y_i-f_1(x_i)]=\frac{1}{3}\sum _{i=1}^3{y}_i-f_1(x)=-0.34$$

$$c_{2,2}=\frac{1}{4}\sum _{i=4}^7[y_i-f_1(x_i)]=\frac{1}{4}[\sum _{i=4}^7{y}_i$$