CTR预估系列(一)-FNN论文笔记

1 论文摘要及介绍

在推荐系统或者广告系统中，CTR、CVR预估至关重要。不同于视觉和音频领域连续的原始特征，这些任务场景的输入特征大多数是多类型的离散特征， 且特征之间相互依赖的先验知识很少。常用的解决方法是线性模型+手工组合高阶特征。线性模型简单有效，但无法学习特征间组合信息。手工组合高阶特征会导致庞大的特征空间，待学习参数量增加，导致模型训练复杂。非线性模型可以通过特征间的组合提高模型的能力，例如FM模型将二值化的特征映射程连续的低维空间，通过內积获取特征间的组合关系；GBDT等梯度提升树算法可以通过树的构建过程自动的学习特征的组合，这些方法都不能利用所有可能的组合关系。DNN在CV和NLP等领域取得较好的效果，而针对CTR预估等场景下大规模输入特征空间下，DNN需要学习的参数量也很大，计算成本较高。

在本论文中，利用有监督或者无监督的Embedding方法来学习大规模多类型的离散特征空间。论文提出的FNN模型中Embedding层采用FM模型来有监督的对稀疏特征进行降维处理，转换为稠密连续型特征。论文提出的SNN-RBM模型采用基于负采样的RBM来处理Embedding层，SNN-DAE则采用基于负采样的DAE处理Embedding层。在Embedding层之上，构建多层的神经网络来探索潜在的数据的模式。

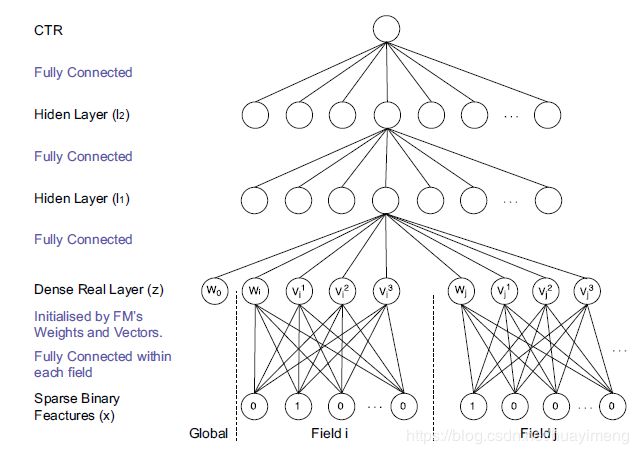
模型输入categorical特征都是field-wis one-hot编码，编码后特征记为: $x$。

2 FNN原理

从上到下，各层定义及说明如下：

输出层：使用$sigmoid(x)=1/\left(1+e^{-x}\right)$激活函数，即：
$$\hat{y}=\mathrm{sigmoid}\left({\mathbf{W}}_3{l}_2+b_3\right)$$
其中，${\mathbf{W}}_3\in {\mathbb{R}}^{1\times L}，b_3\in \mathbb{R}\text{ and }{l}_2\in {\mathbb{R}}^L$

隐藏层l2层、l1层使用$\tanh (x)=\left(1-e^{-\beta x}\right)/\left(1+e^{-2x}\right)$激活函数，即：
$$l_2=\tanh \left(W_2{l}_1+b_2\right)$$

$$l_1=\tanh \left(W_{1}z+b_1\right)$$

其中，${\mathbf{W}}_2\in {\mathbb{R}}^{L\times M},{\mathbf{b}}_2\in {\mathbb{R}}^L，l_1\in {\mathbb{R}}^M$；${\mathbf{W}}_1\in {\mathbb{R}}^{M\times J},{\mathbf{b}}_1\in {\mathbb{R}}^M$ and $\mathbf{z}=\left(w_0,{\mathbf{z}}_1,{\mathbf{z}}_2,\dots {\mathbf{z}}_i,\dots ,{\mathbf{z}}_n\right)\in {\mathbb{R}}^J$，$w_0\in \mathbb{R}$是全局biais参数，$n$是特征类型总数，${\mathbf{z}}_i={\mathbf{W}}_0^i\cdot \mathbf{x}\left[{\mathrm{start}}_i:{\mathrm{end}}_i\right]=\left(w_i,v_i^1,v_i^2,|\dots ,v_i^K\right)$ 代表第i个field特征。$z$向量是上图中第一层，由FM训练得出：
$$y_{\mathrm{F}\mathrm{M}}(\mathbf{x}):=\mathrm{sigmoid}\left(w_0+\sum _{i=1}^N{w}_i{x}_i+\sum _{i=1}^N\sum _{j=i+1}^N⟨{\mathbf{v}}_i,{\mathbf{v}}_j⟩x_i{x}_j\right)$$
上层的神经网络学习的是FM的输出表示，所以大大减少了网络参数，解决了计算复杂度问题。而不同隐层通过采用不同激活函数可以从数据中学习不同形式的表示， 所以模型会更好的捕捉到潜在的组合关系，获得更好的性能。

借鉴CNN通过相邻层神经元进行局部连接来充分利用空间局部相关性的思想，因此，为了保证局部的稀疏性，以及让FM在潜在空间中学习到的结构化数据表示更好用于后续的模型，所以FNN的底层并没有采用全连接。但是FM的乘积规则和DNN的求和规则确实存在明显的差异性，但根据文献，如果观测的差异信息高度不确定，则后边DNN层的权重并不会明显偏离FM层的权重。

另外，除了FM层的隐藏层的权重可以使用文献[17]中提出基于contrastive divergence的layer-wise RBM预训练模型进行初始化，这样可以更有效的保留输入数据的信息。FM层的权重可以使用SGD进行训练，只更新连接非0输入单元的权重，可以大大降低计算复杂度。通过预训练对FM层和其他的层进行初始化之后，使用交叉熵的损失函数进行有监督的fine-tuning(后向传播)：
$$L(y,\hat{y})=-y\log \hat{y}-(1-y)\log (1-\hat{y})$$
通过后向传播的链式法则，包括FM在内的所有FNN权重可以被快速的更新，例如，FM层权重更新方式如下：
$$\begin{array}{rl}\frac{\partial L(y,\hat{y})}{\partial {\mathbf{W}}_0^i}& =\frac{\partial L(y,\hat{y})}{\partial {\mathbf{z}}_i}\frac{\partial {\mathbf{z}}_i}{\partial {\mathbf{W}}_0^i}=\frac{\partial L(y,\hat{y})}{\partial {\mathbf{z}}_i}\mathbf{x}\left[{\mathrm{start}}_i:{\text{ end }}_i\right]\\ {\mathbf{W}}_0^i& \leftarrow {\mathbf{W}}_0^i-\eta \cdot \frac{\partial L(y,\hat{y})}{\partial {\mathbf{z}}_i}\mathbf{x}\left[{\mathrm{start}}_i:{\mathrm{end}}_i\right]\end{array}$$
由于输入$x\left[{\text{ start }}_i:{\text{ end }}_i\right]$特征大多数都是0，所以在fine-tuning过程中只更新连接非0单元的权重。

3 SNN原理

SNN模型和FNN模型的区别主要是在最底层的网络结构和训练方法。SNN的底层采用Sigmoid激活函数的全连接：
$$z=\mathrm{sigmoid}\left(W_{0}x+b_0\right)$$
底层权重的初始化，在预训练阶段尝试了RBM和DAE模型。为了优化高度稀疏one-hot编码带来的计算成本问题，论文提出了基于采样的RBM(SNN-RBM, Fig2(b))，和基于采样的DAE(SNN-DAE，Fig2©)方法来计算底层初始化权重。在训练时，我们不使用每个field的全部的特征，例如city这个领域，只有一个元素是1，其他都是0，所以我们随机采样m个为0的元素，图2中（b）和（c）中的黑点表示的没有被采样到的为0的元素。然后RBM使用对比散度，在DAE上用SGD来进行预训练，得到的稠密的特征表示作为后一层的输入。

4 实验及结论

• 激活函数：尝试了线性函数，sigmoid，tanh，然后发现tanh是最好的

• 结构选择：研究了具有3,4,5个隐层的结构，发现具有3个隐层的结构效果最好。除了增减层数外，我们还对比了不同的结构，在总的隐含节点相同的情况下，发现钻石型的是最好的。最后使用结构是（200,300,100）
  

• 正则化：dropout效果优于L2，dropout的比例的变化，对AUC的影响是比较大的。随着dropout比例的变大，模型的能力先变好，然后显著的下降。对于FNN来说，dropout的最佳值为0.8，对SNN来说，dropout的最佳值为0.99
  

5 参考资料

• Deep Learning over Multi-field Categorical Data - A Case Study on User Response Prediction. Weinan Zhang etc.
• FNN论文解读: https://zhuanlan.zhihu.com/p/65112570
• 论文作者复现代码：https://github.com/wnzhang/deep-ctr